14-6单缝衍射 物理学教程 (第二版) R 衍射角 琅禾费单缝衍射 B 'bsin O (衍射角0:向上为正,向下为负.) 菲涅尔波带法 C=bsn9=场子 (k=1,2,3,…) 第十四章波动光学
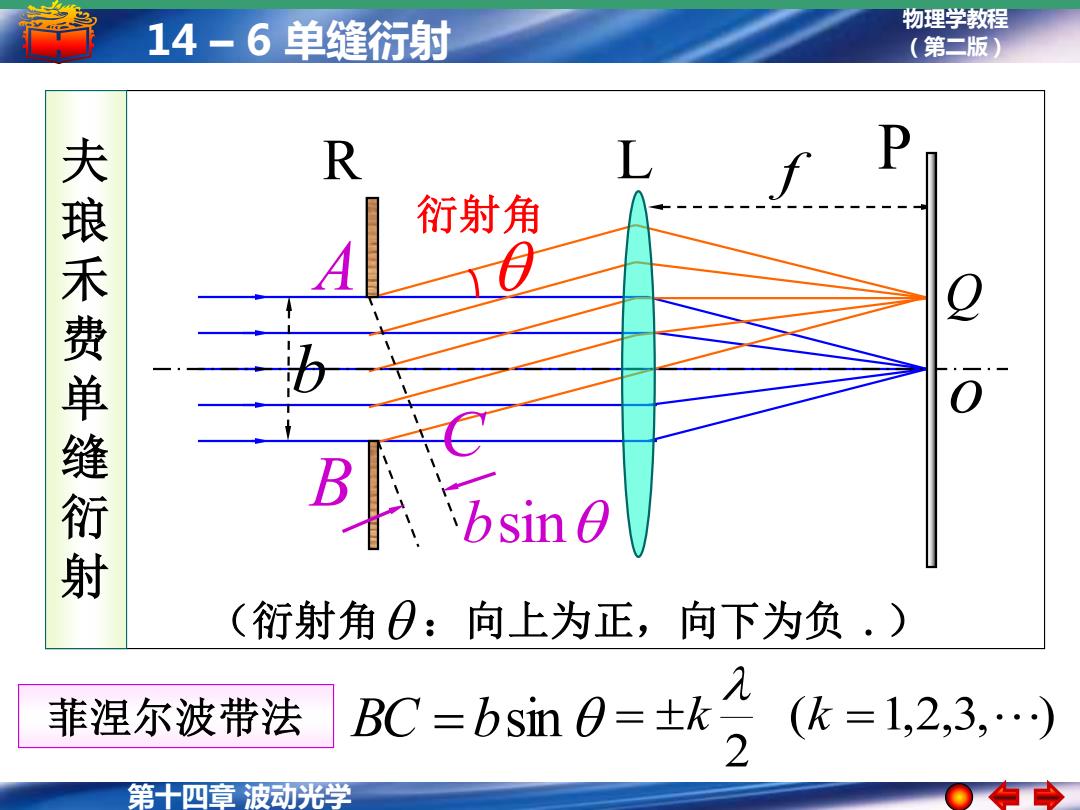
第十四章 波动光学 物理学教程 14 – 6 单缝衍射 (第二版) 夫 琅 禾 费 单 缝 衍 射 衍射角 (衍射角 :向上为正,向下为负 .) b BC = bsin ( 1,2,3, ) 2 = k k = o L f R P A B bsin Q C 菲涅尔波带法

14-6单缝行射 物理学教程 (第二版) 半波带法 R D b B 0 缝长 bsin0=±2k B 元/2 A R b A B bsm0=(2k+103 k=1,2,3,· / 第十四章波动光学
第十四章 波动光学 物理学教程 14 – 6 单缝衍射 (第二版) o R P A B Q 2 bsin = 2k 2 bsin = (2k +1) 一 半波带法 k =1,2,3, A1 A2 C / 2 b A B b 缝长 A B o A Q B R L P C A1 / 2 L
14-6单缝衍射 物理学教程 (第二版) R P BC=bsin 0 几 ±k 2 B (k个半波带) bsin=0 中央明纹中心 bsin0=±2k =士k干涉相消(暗纹) 2k个半波带 2 bsim0=±(2k+02 干涉加强 (明纹) 2k+1 个半波带 人bsn0+k (介于明暗之间) (k=1,2,3,) 第十四章波动光学
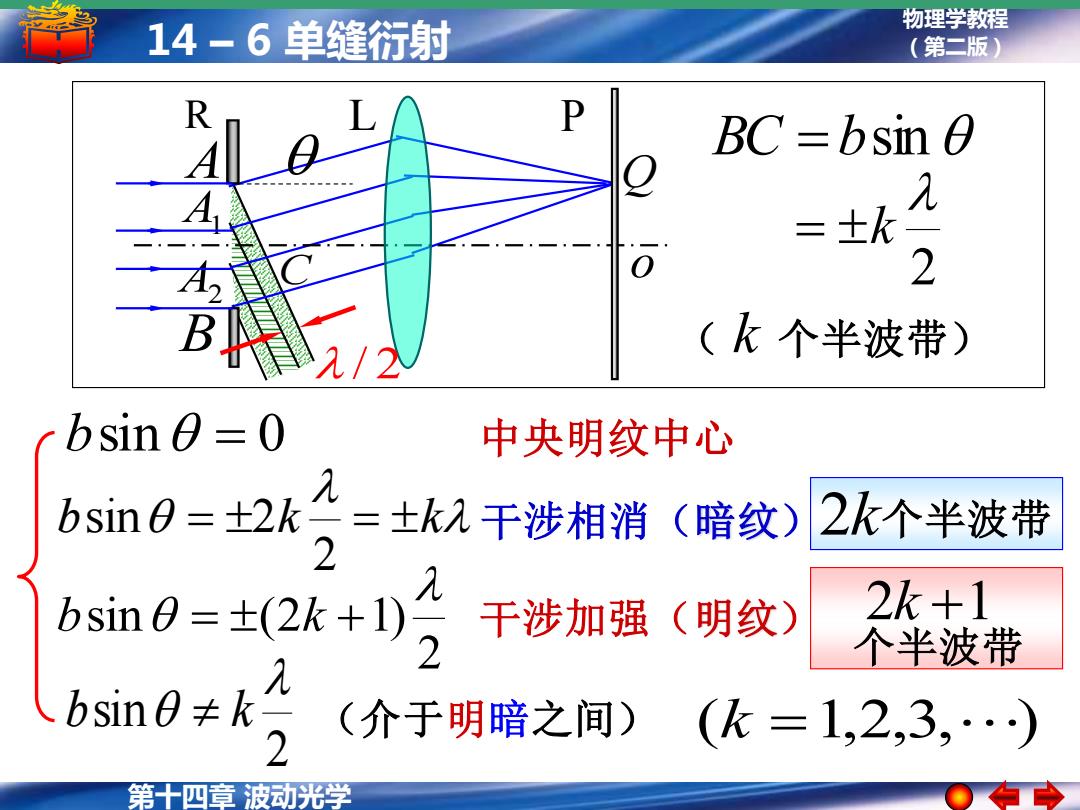
第十四章 波动光学 物理学教程 14 – 6 单缝衍射 (第二版) (k =1,2,3, ) b = k = k 2 sin 2 干涉相消(暗纹) 2 sin (2 1) b = k + 干涉加强(明纹) 2 sin b k (介于明暗之间) L o R P A Q B A1 A2 C / 2 BC = bsin 2 = k ( k 个半波带) 2k 个半波带 个半波带 2k +1 bsin = 0 中央明纹中心
14-6单缝行射 物理学教程 (第二版) 二 光强分布 〔bsin0=±2k=±k 干涉相消(暗纹) 2 bsin8=±(2k+102 干涉加强(明纹) si0 第十四章波动光学
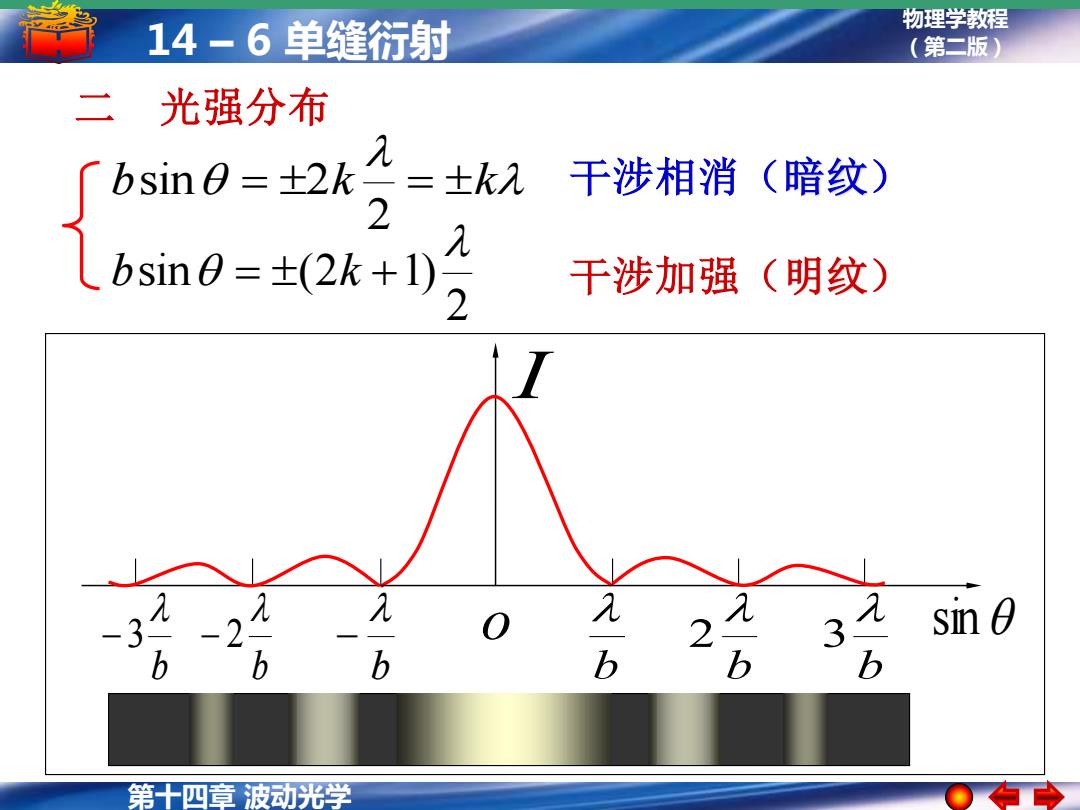
第十四章 波动光学 物理学教程 14 – 6 单缝衍射 (第二版) sin I o b b 2 b 3 b − b − 2 b − 3 二 光强分布 b = k = k 2 sin 2 干涉相消(暗纹) 2 sin (2 1) b = k + 干涉加强(明纹)

14-6单缝衍射 物理学教程 (第二版) R X X 当O较小时,sin0≈0 xX= 元 2 3 si O b b b 2 3 X b b 第十四章波动光学 点
第十四章 波动光学 物理学教程 14 – 6 单缝衍射 (第二版) sin I o b b 2 b 3 b − b − 2 b − 3 L1 L2 f b S R P O x x sin x =f 当 较小时, f x b f b − f b f 2 b f − 2 b − 3 f b 3