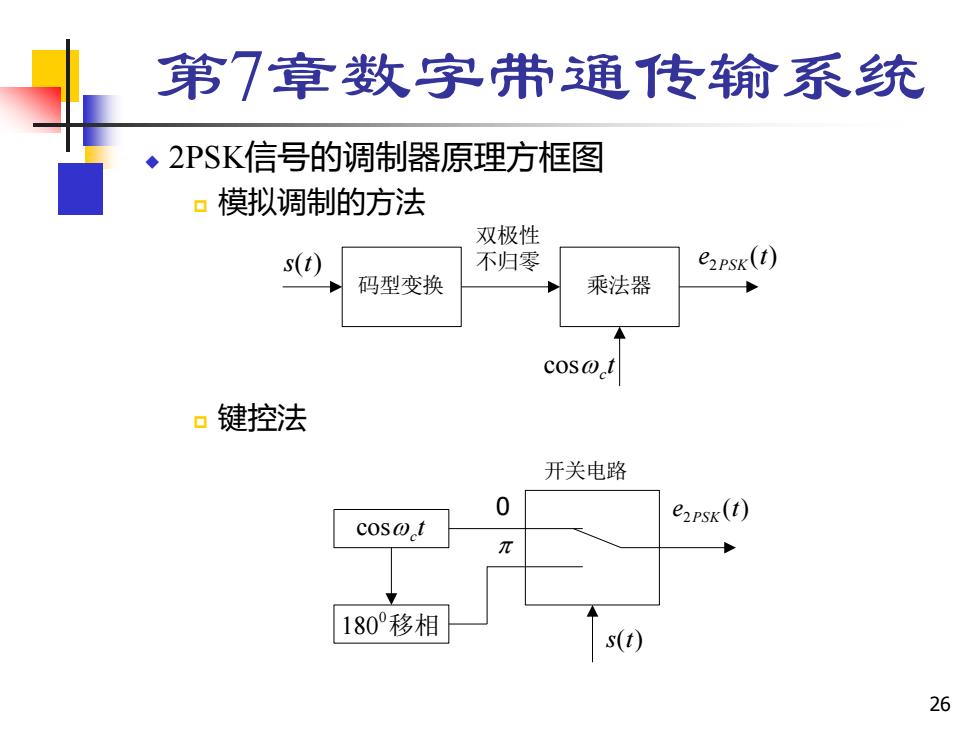
第7章数字带通传输系统 ◆2PSK信号的调制器原理方框图 。模拟调制的方法 双极性 s(t) 不归零 e2psk(1) 码型变换 乘法器 口键控法 开关电路 0 e2psk(1) coso t π 180°移相 s(t) 26
26 第7章数字带通传输系统 ◆ 2PSK信号的调制器原理方框图 模拟调制的方法 键控法 乘法器 ( ) 2 e t PSK 双极性 不归零 t c cos s(t) 码型变换t c cos s(t) ( ) 2 e t PSK 开关电路 1800移相 0
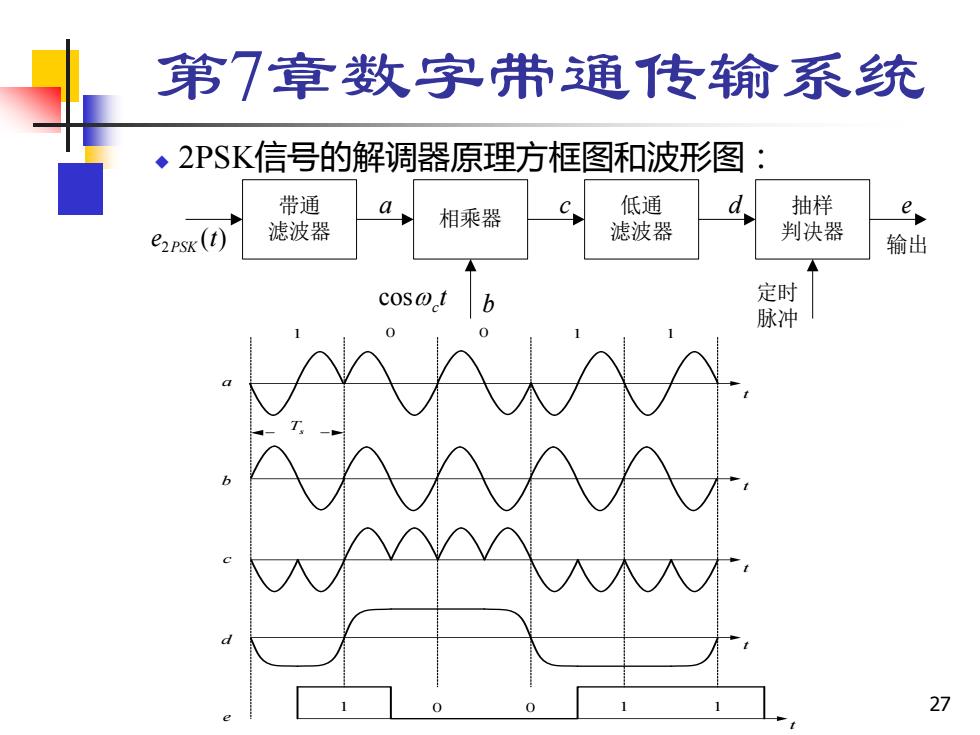
第7章数字带通传输系统 ◆2PSK信号的解调器原理方框图和波形图 带通 a C 低通 d 相乘器 抽样 e e2rsK(t) 滤波器 滤波器 判决器 输出 cos@t 定时 脉冲 0 27
27 第7章数字带通传输系统 ◆ 2PSK信号的解调器原理方框图和波形图: 带通 滤波器 相乘器 低通 滤波器 抽样 判决器 定时 脉冲 e2PSK (t) 输出 t c cos a b c d e 1 0 0 1 T s t a bc d 1 t t t t e 1 0 0 1 1

第7章数字带通传输系统 波形图中,由于在2PSK信号的载波恢复过程中存在着的相 位模糊,即恢复的本地载波与所需的相干载波可能同相, 也可能反相,这种相位关系的不确定性将会造成解调出的 数字基带信号与发送的数字基带信号正好相反,即“1变 为"0”,"0变为“1”,判决器输出数字信号全部出错。 这种现象称为2PSK方式的“倒π”现象或“反相工作”。 这也是2PSK方式在实际中很少采用的主要原因。另外,在 随机信号码元序列中,信号波形有可能出现长时间连续的 正弦波形,致使在接收端无法辨认信号码元的起止时刻。 为了解决上述问题,可以采用7.1.4节中将要讨论的差 分相移键控(DPSK)体制。 28
28 第7章数字带通传输系统 波形图中,由于在2PSK信号的载波恢复过程中存在着的相 位模糊,即恢复的本地载波与所需的相干载波可能同相, 也可能反相,这种相位关系的不确定性将会造成解调出的 数字基带信号与发送的数字基带信号正好相反,即“1”变 为“0”,“0”变为“1”,判决器输出数字信号全部出错。 这种现象称为2PSK 方式的“倒π”现象或“反相工作”。 这也是2PSK方式在实际中很少采用的主要原因。另外,在 随机信号码元序列中,信号波形有可能出现长时间连续的 正弦波形,致使在接收端无法辨认信号码元的起止时刻。 为了解决上述问题,可以采用7.1.4节中将要讨论的差 分相移键控(DPSK)体制

第7章数字带通传输系统 ◆功率谱密度 比较2ASK信号的表达式和2PSK信号的表达式: 2ASK:e2ASK(1)=s(t)cos@t 2PSK:e 概率为P -Acos@t,概率为1-P 可知,两者的表示形式完全一样,区别仅在于基带信号() 不同(αm不同),前者为单极性,后者为双极性。因此, 我们可以直接引用2ASK信号功率谱密度的公式来表述 2PSK信号的功率谱,即 Pms(f)=i[P(+)+P.(f-S 29
29 第7章数字带通传输系统 ◆ 功率谱密度 比较2ASK信号的表达式和2PSK信号的表达式: 2ASK: 2PSK: 可知,两者的表示形式完全一样,区别仅在于基带信号s(t) 不同(an不同),前者为单极性,后者为双极性。因此, 我们可以直接引用2ASK信号功率谱密度的公式来表述 2PSK信号的功率谱,即 e t s(t) t c ( ) cos 2ASK = − − = t P t P e t c c Acos , 1 Acos , ( ) 2PSK 概率为 概率为 ( ) ( ) 4 1 ( ) 2PSK s c s c P f = P f + f + P f − f

第7章数字带通传输系统 由6.1.2节知,双极性的全占空矩形随机脉冲序列的功率谱 密度为 P.(f)=4f:P1-P)G(f)2+f1-2P)2G(0)6f) 将其代入上式,得 Papsk =f,P(I-P)G(f+f)+G(f-f.) +1-2PlG0y6f+)+-1.】 若P=1/2,并考虑到矩形脉冲的频谱: Gf)=T,Sa(πfT3) G(0)=Ts 则2PSK信号的功率谱密度为 -爱∵ 30
30 第7章数字带通传输系统 由6.1.2节知,双极性的全占空矩形随机脉冲序列的功率谱 密度为 将其代入上式,得 若P =1/2,并考虑到矩形脉冲的频谱: 则2PSK信号的功率谱密度为 ( ) 4 (1 ) ( ) (1 2 ) (0) ( ) 2 2 2 2 P f f P P G f f P G f s = s − + s − (1 2 ) (0) ( ) ( ) 4 1 (1 ) ( ) ( ) 2 2 2 2 2 2PSK s c c s c c f P G f f f f P f P P G f f G f f + − + + − = − + + − ( ) ( ) S TS G f = T Sa f G = TS (0) − − + + + = 2 2 2 ( ) sin ( ) ( ) sin ( ) 4 ( ) c s c s c s s c s PSK f f T f f T f f T T f f T P f