
Actions of A LR-Parser 1.shift s --shifts the next input symbol and the state s onto the stack (SoX1 S1...Xm Sm:ai aiti ..an $)(SoX1 S1...Xm Smais,ai+i ...an$) 2.reduce A->B (or rn where n is a production number) - pop 2B (=r)items from the stack; - then push A and s where s=goto[sm-r,A] (So X1 S1...Xm Sm>ai ai+l..an$)So X1 S1...Xm-r Sm-r As,ai...an $ Output is the reducing production reduce A->B 3.Accept-Parsing successfully completed 4.Error --Parser detected an error(an empty entry in the action table) CS308 Compiler Theory 16
Actions of A LR-Parser 1. shift s -- shifts the next input symbol and the state s onto the stack ( S o X1 S1 ... X m S m, ai ai+1 ... a n $ ) Î ( S o X1 S1 ... X m Sm ai s, ai+1 ... a n $ ) 2. re duce A→β (or rn wh i d ti b ) here n is a pro duction num ber ) – pop 2| β| (=r) items from the stack; – then push then push A and s where s=goto[s s=goto[sm-r,A] ( S o X1 S1 ... X m S m, ai ai+1 ... a n $ ) Î ( S o X1 S1 ... Xm-r Sm-r A s, ai ... a n $ ) – Output is the reducing production reduce A→β 3. Accept – Parsing successfully complete d 4 E P d t t d ( t t i th ti t bl ) CS308 Compiler Theory 16 . Error -- Parser d e tec t e d an error (an emp ty en try in the action t abl e )

Reduce Action ·pop2lβl(=r)items from the stack;let us assume that阝=Y,Y2..Yr 。 then push A and s where s=goto[sm-A] (SoX1S1...Xm-r Sm-r YI Sm-rYrSm:ai aitl.an) →(SoX1S1.Xm-rSm-rAs,ai…an$) In fact,Y Y2...Y,is a handle. X1...Xm-r A ai...an sx1..Xm Y1...Yr ai aiti...an S CS308 Compiler Theory
Reduce Action • pop 2|β| (=r) items from the stack; let us assume that β = Y1Y2...Yr • then push A and s where s=goto[sm-r,A] ( So X1 S1 ... Xm r Sm r Y1 Sm r ...Yr Sm, ai ai+1 ... a ( S n $ ) o X1 S1 ... Xm-r Sm-r Y1 Sm-r ...Yr Sm, ai ai+1 ... an $ ) Î ( So X1 S1 ... Xm-r Sm-r A s, ai ... an $ ) • In fact, Y1Y2...Yr is a handle. X1 ... Xm-r A ai ... an $ ⇒ X1 ... Xm Y1...Yr ai ai+1 ... an $ CS308 Compiler Theory 17
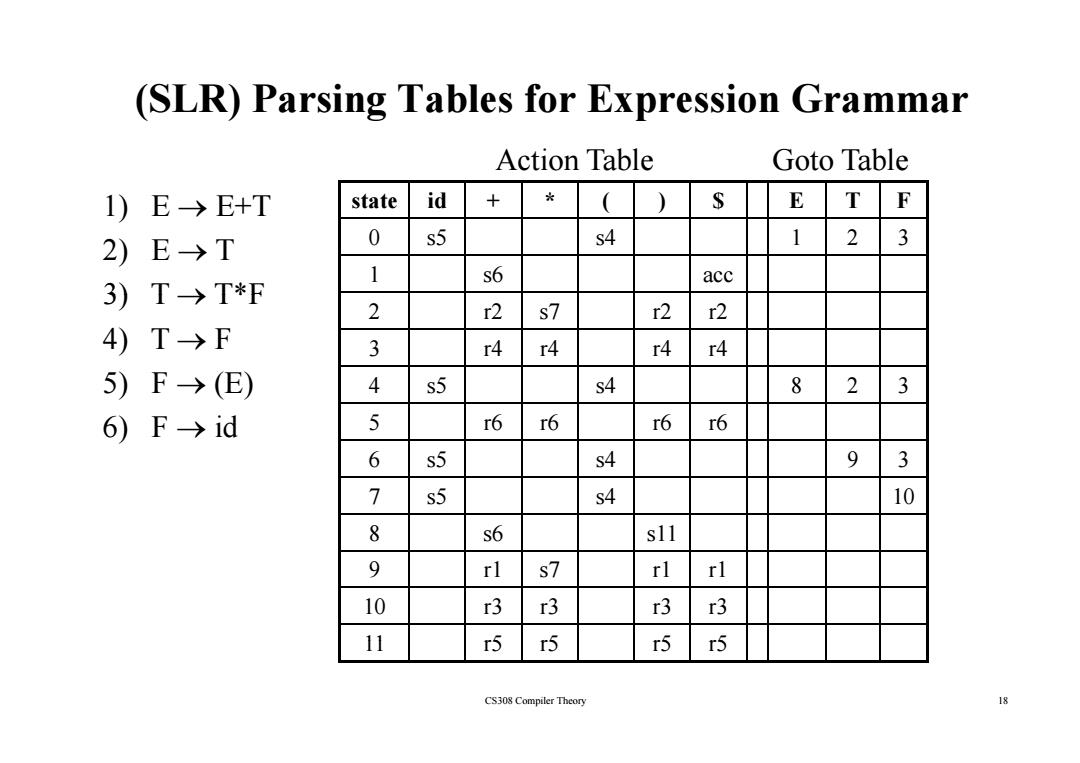
(SLR)Parsing Tables for Expression Grammar Action Table Goto Table 1)E→E+T state id + ( S E T F 2)E→T 0 s5 s4 1 2 3 1 s6 acc 3)T→T*F 2 r2 s7 r2 r2 4)T→F 3 r4 r4 r4 r4 5)F→(E) 4 s5 s4 8 2 3 6)F→id 5 r6 r6 r6 T6 6 s5 s4 9 3 7 s5 s4 10 8 s6 s11 9 rl s7 rl rl 10 r3 r3 r3 r3 11 r5 r5 r5 r5 CS308 Compiler Theory 18
(SLR) Parsing Tables for Expression Grammar state id + * ( ) $ E T F Action Table Goto Table 1) E → E+T state id ( ) $ E T F 0 s5 s4 1 2 3 1 s6 acc 1) E → E+T 2) E → T 3) T → T*F 2 r2 s7 r2 r2 3 r4 r4 r4 r4 4 5 4 8 2 3 3) T → T*F 4) T → F 5) F → (E) 4 s 5 s 4 8 2 3 5 r6 r6 r6 r6 6 s5 s4 9 3 5) F → (E) 6) F → id 7 s5 s4 10 8 s6 s11 9 r1 s7 r1 r1 10 r3 r3 r3 r3 11 r5 r5 r5 r5 CS308 Compiler Theory 18 11 r5 r5 r5 r5

Actions of A (S)LR-Parser--Example stack input action output 0 id*id+idS shift 5 Oid5 *id+idS reduce by F-→id F-→id 0F3 *id+idS reduce by T→F T→F 0T2 *id+idS shift 7 0T2*7 id+idS shift 5 0T2*7id5 +idS reduce by F→id F→id 0T2*7F10 +idS reduce by T→T*F T→T*F 0T2 +idS reduce by E-→T E→T 0E1 +idS shift 6 0E1+6 idS shift 5 0E1+6id5 $ reduce by F→id F→id 0E1+6F3 $ reduce by T→F T→F 0E1+6T9 $ reduce by E-→E+T E→E+T 0E1 $ accept CS308 Compiler Theory 19
Actions of A (S)LR-Parser -- Example stack input action output 0 id*id+id$ shift 5 shift 5 0id5 *id+id$ reduce by F →id F →id 0F3 *id+id$ reduce by T →F T → F 0T2 *id+id$ shift 7 0T2*7 id+id$ shift 5 0T2 7id5 * +id$ reduce by F reduce by F →id F →id 0T2*7F10 +id$ reduce by T →T*F T →T*F 0T2 +id$ reduce by E →T E → T 0E1 +id $ shift 6 0E1+6 id$ shift 5 0E1+6id5 $ reduce b y F →id F →id 0E1+6F3 $ reduce by T →F T → F 0E1+6T9 $ reduce by E →E+T E →E+T 0E1 $ accept CS308 Compiler Theory 19

Constructing SLR Parsing Tables-LR(O)Item An LR(0)item of a grammar G is a production of G a dot at the some position of the right side. ·Ex:A→aBb Possible LR(O)Items: A→。aBb (four different possibility) A→a。Bb A→aB.b A→aBb。 Sets of LR(O)items will be the states of action and goto table of the SLR parser. A collection of sets of LR(O)items (the canonical LR(0)collection)is the basis for constructing SLR parsers. ·Augmented Grammar: G'is G with a new production rule S'->S where S'is the new starting symbol. CS308 Compiler Theory 20
Constructing SLR Parsing Tables – LR(0) Item • An LR(0) item of a grammar G is a production of G a dot at the some posi i f h i h id i t ion o f t he r i g ht side. • Ex: A → aBb Possible LR(0) Items: A → .aBb (four different possibility) (four different possibility) A → a .Bb A → aB . b A → aBb . • Sets of LR(0) items will be the states of action and goto table of the SLR parser. • A collection of sets of LR(0) items (the canonical LR(0) collection) is the basis for constructing SLR parsers. • Augmented Grammar: G’ is G with a new production rule S’ →S where S’ is the new starting b l CS308 Compiler Theory 20 sym b o l