
0=-2h2vv'(1-cos0)+2mghc(v-v') hvv'(1-cose)=mc2(v-v) 0-w0-99 m.c 0-mM=-入 △2=1(1-c0s0) λc= h=0.0242621A Compton波长,对应 mc 于静止电子的波长
2 2 0 0 2 (1 cos ) 2 ( ) h m hc 2 0 h m c (1 cos ) ( ) 0 (1 cos ) h c c m c 0 (1 cos ) h m c (1 cos ) C 0.0242621A 0 m c h C Compton波长,对应 于静止电子的波长

§2.1不确定关系 ·1、波粒二象性 光子能量:E=hv 光子 质量:m=hv/c 光子动量: p=E/c=hv/c=h/λ ·粒子性:一个光子是一个不可分割的主体 。氵 波动性:具有波的特征,入=h/p ·光同时具有波动性和粒子性
§2.1 不确定关系 • 1、波粒二象性 • 光子能量: = h 光子 质量:m=h /c 2 光子动量: p=E/c=h /c=h / • 粒子性 :一个光子是一个不可分割的主体 • 波动性: 具有波的特征, =h /p • 光同时具有波动性和粒子性

粒子的波动性 ·de Broglie物质波 ·1924年,de Broglie将Einstein的光 量子概念推广,提出了物质波的概 念 ·所有的波都具有粒子性 ·所有的粒子都具有波动性 ·2=hp ·p=mw/(1-y2/c2)12 Prince Louis-victor de ·不能将物质的运动和波的传播分开。 Broglie 1892-1987
粒子的波动性 • de Broglie物质波 • 1924年,de Broglie将Einstein的光 量子概念推广,提出了物质波的概 念 • 所有的波都具有粒子性 • 所有的粒子都具有波动性 • =h /p • p=mv/(1-v 2 /c 2 ) 1/2 • 不能将物质的运动和波的传播分开。 Prince Louis-victor de Broglie 1892-1987

·波粒二象性的物理本质 ·1、不能理解为经典意义下的波或粒子 经典波:物理量在空间的周期性分布 ·经典粒子:具有确定位置、轨迹、速度的实物 ·2、应当理解为: 粒子性:本身所具有的颗粒性质,或作为一个整 体的不可分割性 ·波动性:物理量、或状态是可以线性叠加的 ·可以通过具体的实例理解波粒二象性
• 波粒二象性的物理本质 • 1、不能理解为经典意义下的波或粒子 • 经典波:物理量在空间的周期性分布 • 经典粒子:具有确定位置、轨迹、速度的实物 • 2、应当理解为: • 粒子性:本身所具有的颗粒性质,或作为一个整 体的不可分割性 • 波动性:物理量、或状态是可以线性叠加的 • 可以通过具体的实例理解波粒二象性
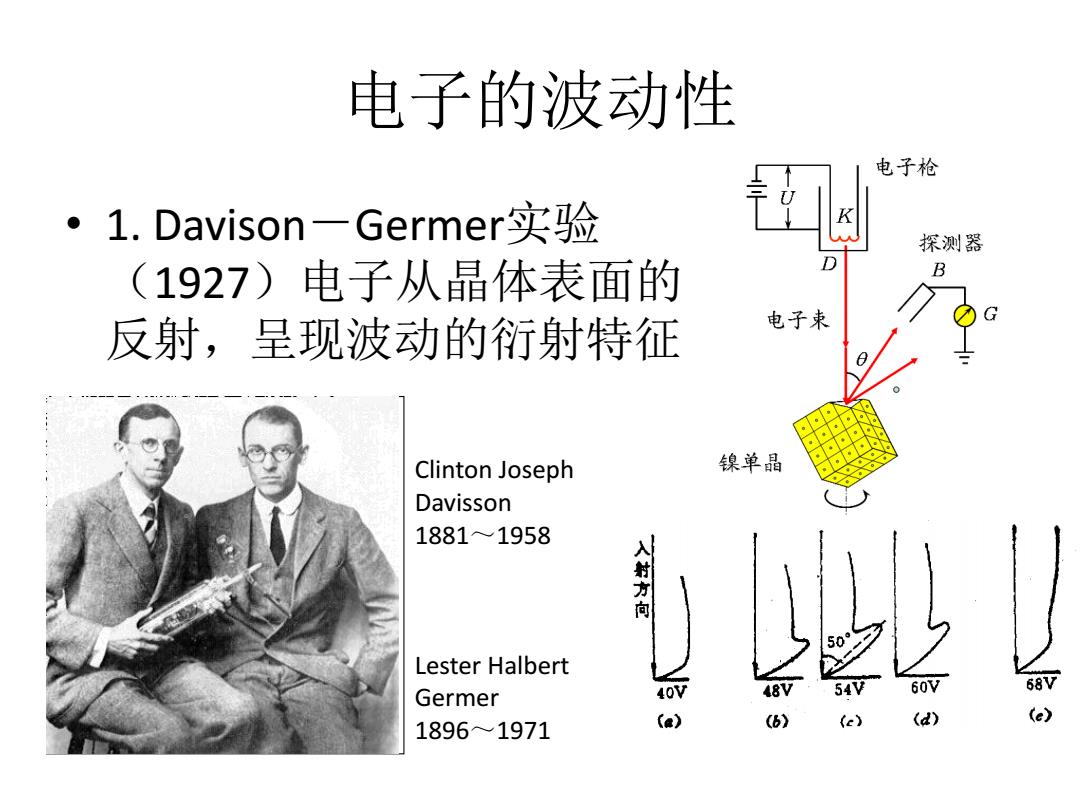
电子的波动性 电子枪 ·1.Davison一Germer实验 探测器 (1927)电子从晶体表面的 B 反射,呈现波动的衍射特征 电子束 Clinton Joseph 镍单晶 Davisson 1881~1958 入射方向 Lester Halbert 40V 48V 54 60 68V Germer 1896~1971 (a) (6) (e) (d) (e)
电子的波动性 • 1. Davison-Germer实验 (1927)电子从晶体表面的 反射,呈现波动的衍射特征 Clinton Joseph Davisson 1881~1958 Lester Halbert Germer 1896~1971