
第一章绪论 功率消耗小,动作速度快.无机械转动部分,称之为电子式静态保护装置。随着大 规模集成电路的发展,80年代后期,集成电路继电保护装置很快取代了品体管继 电保护装置,成为静态继电保护装置的主要型式。 在60年代末,电子计算机一问世,便进行了对继电保护计算机算法的大量研 究,为今天微型计算机式继电保护(以下简称微机继电保护)的发展奠定了理论基 础。随若微处理器技术的迅速发展及其价格急制下降,在70年代后期,出现了比 较完普的微机保护样机,并投入到电力系统中试运行。80年代微机保护在硬件结 构和软件技术方面已趋成熟。微机保护具有巨大的计算、分析和逻辑判断能力,有 存储记忆功能,因而可用以实现任何性能完善且复杂的保护原理。微机继电保扩 可连续不断地对本身的工作情况进行自检,其工作可靠性很高。此外,微机继电保 护可用同-硬件实现不同的保护原琪,这使保护装置的制造大为简化,也容易实行 保护装管的标准化。微机继电保护除了共有保护功能外,还有故障录波、故障测 距、事件顺序记录,以及与调度计算机交换信息等辅助功能,这对于简化保护的调 试、事故分析和事故后的处理等都有重大意义。进入20世纪90年代以来,在我国 得到大量应用,已成为继电保护装置的主要型式,是当今电力系统保护,控制、运行 阔度及事歧处理的综合自动化系统的重要组成部分。 随着计算机技术、微电子技术,网络通信技术、信息技术的不断发展,最新研制 的微机继电保护的体积更小,功能更强,性能更优,如硬件结构方面,采用具有强大 数据处理功能的DSP微处理芯片,低功耗编程逻辑芯片(CPLD)和高集成度专 用芯片(ASIC)后,使装登的体积,功耗,可靠性等方面得到很大提升。我国微机继 电保护正向微型化、网络化,智能化和人性化方面高速发展

第二章微型计算机继电保护的数字信号基础 微型计算机继电保护(微机继电保护)以做型计算机为基础,用数字电路代替 传统的模拟电路,用数字信号处理技术来完成各种计算和逻辑功能。模拟信号的 数字化及处理技术是微机继电保护的重要基础,因此有必要对数字信号的一些基 本概念及处理技术作简要介绍。 2.1采样定理 计算机能接受和处理的是数字信号,而电力系统现场多是模拟信号,因此两种 信号有一个转换的过程,这就是我们常说的采样和AD转换。 所谓采样,即是将连续时间信号变为对应的离散数字信号的过程。 将时间上连续的模拟信号转换成与之对应的在时间上离散的数字信号的理论 基础就是采样定理。采样定理的内容是:对连续时间信号x(t)进行采样时,胤期 采样颍率人,必须大于被采样原始信号x(:)的最大截止频率。的两倍,才能从离 散的数字信号x,(t)中完全恢复出原始信号x(t)。换句话说,当厂>2f时,采样 信号x,(t)完全能代表原始信号x(:),但前提是x(t)的频诺x()是有限带宽 (即当引f>f,2时,有x(f)=0):x(f)=0时的信号频率f即为x《)的最大截 止频率)。 下面就信号的采样和恢复进行讨论。 2.1.1连续时间信号的采样 如图2-1所示,对于一个连续时间的信号x(),如果按等时间间隔T对其进 行采样后,得到的采样脉冲序列就是采样信号。如果用x(:)代表连续时间信号, 则令了,()代表采样信号,下标s表示经过采样后的函数是离散型函数,这样,我 们可以把采样数据信号x,(t)看成是x(t)与脉冲序列8(:)的乘积。 x,(t)=x(t)·6r(t) (2-1) 采样器也可看成是一个调制器,输入量x(t)作为被调制信号,单位脉冲序列 7(t)则看成是载波,如图2-1(b)所示,可以将脉冲序列写成 (t)=8(t-kT)(k=-0,…,-1,0,1,2,…,)(2-2)

第一章薇型计算机继电保护的数字信号基础 9 式中,(t-T)是发生在t=T时刻上的单位脉冲函数。 所以,对连续时间信号x()进行周期采样时,采样信号x.(:)的表达式为 x.(t)=x()∑8(t-kT) (k=-0,…,-1,0,1,2,…,∞)(23) 由于x,(t)是采样开关之后的脉冲序列,只有在采样脉冲出现时刻才有意义: 所以上式也可写成 x(t)=∑x(T)6(1-kT)(k=-如,…,一1,0,1,2,…,∞) (2-4) 0 tttt进 十湖 f 现 图2】利用脉神进行采样得到的采样信号 但是,在实际控制系统中,t<0时,x(t)=0,所以式(2-3)和式(2-4)中尾的取 值范围又可写成 x,(t)=x(t)8(t-T)(k=0,1,2,,o) (2-5) r.()=∑x(kT)t-T)(k=0,1,2,,0) =x(0)8(t)+x(T)8(t-T)+x(2T)8(t-2T)+…(2-6) 式(25)和(26)就是采样信号x,(:)的两种数学描述表达式,它表明了在不同的采 样时刻上有一个脉冲输出,而脉冲的值由该时刻上x(:)的值x(kT)决定。 2,1.2采样信号x。(t)的频谱 在时域上,我们能清楚地看到连续时间信号x()与离散时间信号x,(t)之间 的联系和区别。那么,在频城上,两者频谱之间的关系怎样呢?

电力系统继电保护原理及新技术 对于连续时间信号x(t),其傅甲叶变换X(f)定义为 ((ead (2-7) 对于离散时间信号x,(),其傅里叶变换X()表达式为 X.)(t)8:(heds (2-8) 对」周期函数,用傅里叶级数形式表示为 6r(2)=>Ce2'(n=-0,…,0,1,…,to) (2-9) 式:f=示,称为采样频率,”为采样脉冲(单位冲击脉冲)数 C.( (()e seu - (2-10) 所以有 6r()=()e24(n=-0.…,-1,0,1,2,…,9)2-1) 于是,x,(:)的傅里叶变换表达式为 X(f=()∑xu)p2。ndh -(rt)en dt =≥Xf-n,) (n=-∞,…,-1,0,1,2,…,)2-12) 式中,X(f)是x(t)的傅里叶变换。 通过式(2-12)可以清楚地看出,一个连续时间信号x(:),经过采样后,得到的 采样信号1,)的傅单叶变换其频诣X,(f)与X(f)之间的关系如图2-2所示。 2.1.3采样信号的恢复 下面讨论在满足采样定理的条件下,如何从采样信号【,(x)来复现x(:)的间
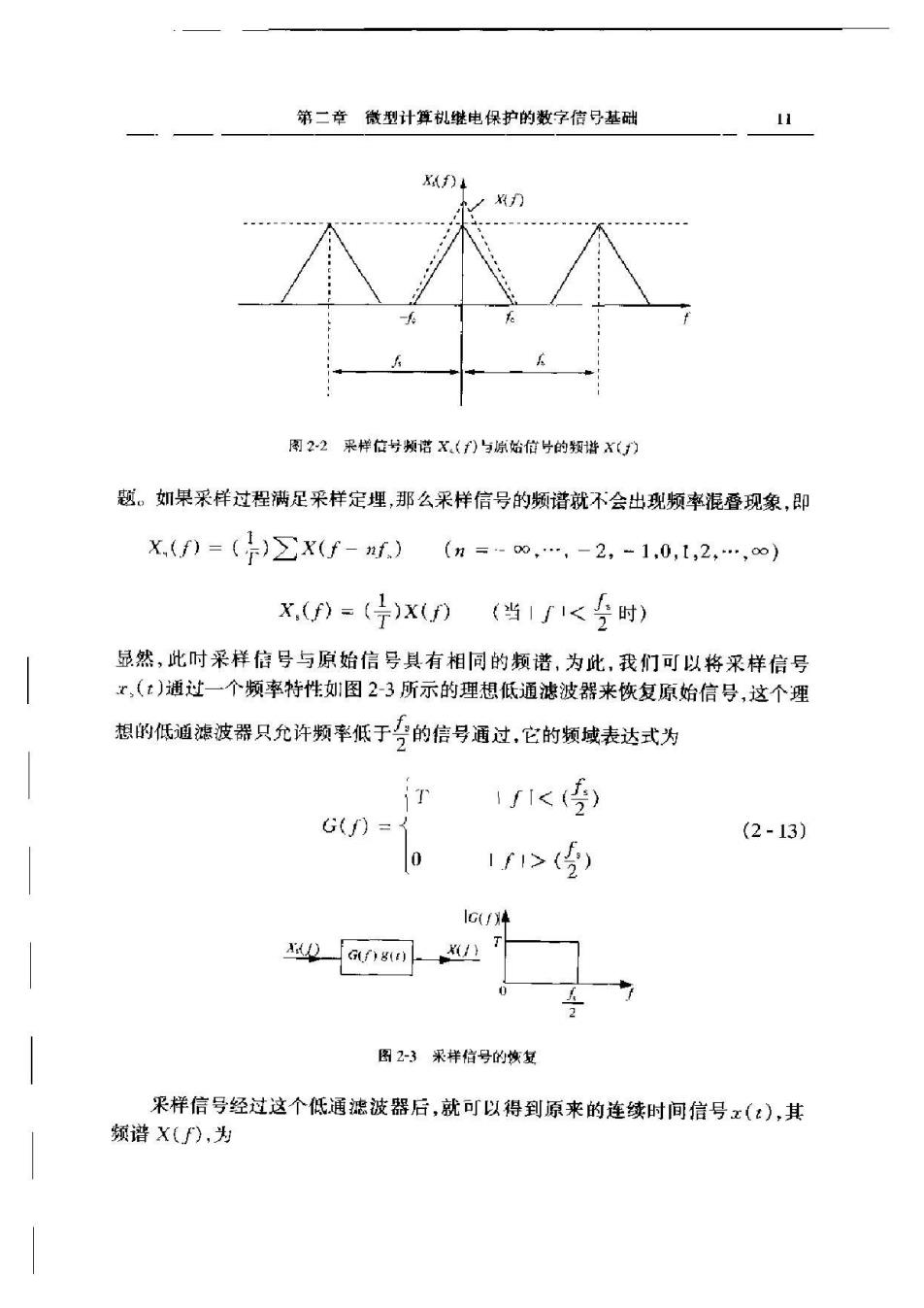
第二章微型计算机继电保护的数字信号基础 11 图22采样位号频诺X,()与原始信号的频谐X() 题。如果采样过程满足采样定埋,那么采样信号的频谱就不会出现频率混叠现象,即 X(f)=(F)∑X(f-nf)(n=-o,…,-2,-1.0,【,2,…,o∞) X,()=(号)xD(当1f1<5时) 显然,此时采样信号与原始信号具有相同的频谐,为此,我们可以将采样信号 x,(t)通过一个频率特性如!图2-3所示的理想低通滤波器来恢复原始信号,这个理 想的低通滤波器只允许频率低于号的信号通过,它的频域表达式为 1f1<) (2-13) 1f1>(5) Gf年 周23果样信号的恢复 采样信号经过这个低通滤波器后,就可以得到原来的连续时间信号x(:),其 频谱X(f),为