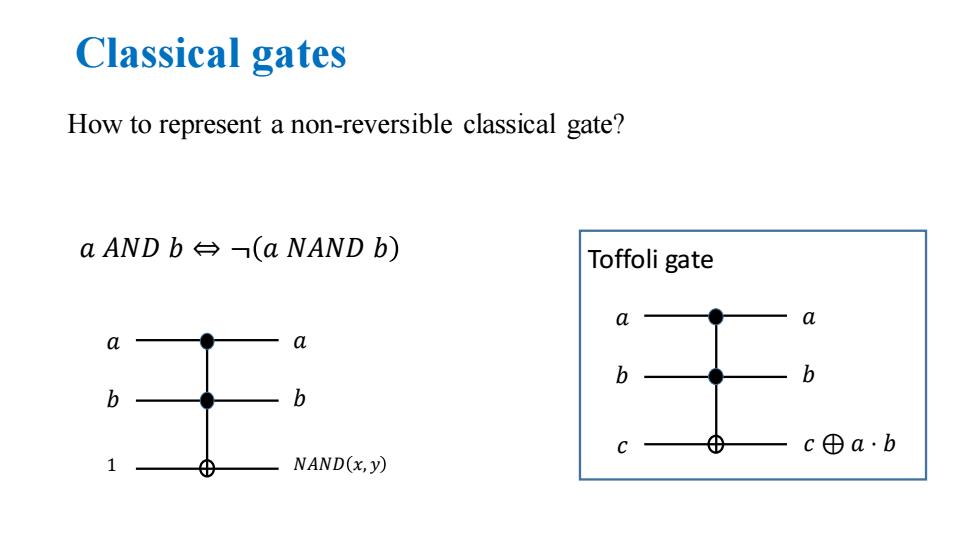
Classical gates How to represent a non-reversible classical gate? a AND b台-(a NAND b) Toffoli gate a a a a b b b c ⊕ c⊕a·b NAND(x,y)
Classical gates 𝑎 𝑏 𝑐 𝑎 𝑏 𝑐 ⊕ 𝑎 ⋅ 𝑏 Toffoli gate 𝑎 𝐴𝑁𝐷 𝑏 ⇔ ¬ 𝑎 𝑁𝐴𝑁𝐷 𝑏 𝑎 𝑏 1 𝑎 𝑏 𝑁𝐴𝑁𝐷 𝑥, 𝑦 How to represent a non-reversible classical gate?

Quantum gates Operators. Pauli operators:=();X=();Y=();Z=() XI0〉=11):XI1〉=10;Z10〉=10):Z11)=-|1〉 Y=ixZ;XY=-YX;XZ=-ZX;YZ=-ZY HXH Z;HZH =X;HYH=-Y Controlled gate(C-U)lb〉⑧l〉=lb)⑧Ublp〉 Controlled-U CNOT
Quantum gates • Operators. Pauli operators 𝐼: = 1 0 0 1 ; 𝑋 ≔ 0 1 1 0 ; 𝑌 = 0 𝑖 −𝑖 0 ; 𝑍 = 1 0 0 −1 𝑋 0 = 1 ;𝑋 1 = 0 ; 𝑍 0 = 0 ;𝑍 1 = − 1 𝑌 = 𝑖𝑋𝑍; 𝑋𝑌 = −𝑌𝑋; 𝑋𝑍 = −𝑍𝑋; 𝑌𝑍 = −𝑍𝑌 𝐻𝑋𝐻 = 𝑍; 𝐻𝑍𝐻 = 𝑋; 𝐻𝑌𝐻 = −𝑌 Controlled gate 𝑈 Controlled-U CNOT 𝐶 − 𝑈 𝑏 ⊗ 𝜓 ≔ 𝑏 ⊗ 𝑈 𝑏 |𝜓⟩

Universality of Hadamard+phase+CNOT+T Theorem.Any quantum gate can be approximated by the compositions of the following gates to an arbitrarily small precision H):5=():T=(0p).CNOT Theorem (Solovay-Kitaev).Any n-qubit quantum gate can be approximated to precision s using 0(n24n log(n24m/))gates!. Use a different set of universal gates
Universality of Hadamard+phase+CNOT+T Theorem. Any quantum gate can be approximated by the compositions of the following gates to an arbitrarily small precision H ≔ 1 2 1 1 1 −1 ; 𝑆 = 1 0 0 𝑖 ; 𝑇 = 1 0 0 exp(𝑖𝜋/4) , CNOT Theorem (Solovay-Kitaev). Any 𝑛-qubit quantum gate can be approximated to precision 𝜀 using 𝑂 𝑛 24 𝑛 log𝑐 𝑛 24 𝑛 /𝜀 gates1 . 1Use a different set of universal gates

Complexity perspective P:deterministically polynomial-time computable by a classical computer BPP:probabilistically polynomial-time computable by a classical computer NP:polynomial-time verifiable by a classical computer BQP:probabilistically polynomial-time computable by a quantum computer PSPACE:polynomial-space computable by a classical computer Theorem: Conjecture: PSPACE ·P∈NP∈PSPACE ·P∈BPP∈BQP∈PSPACE BOP NP P=BPP
Complexity perspective P : deterministically polynomial-time computable by a classical computer BPP: probabilistically polynomial-time computable by a classical computer NP: polynomial-time verifiable by a classical computer BQP: probabilistically polynomial-time computable by a quantum computer PSPACE: polynomial-space computable by a classical computer Theorem : • 𝐏 ⊆ 𝐍𝐏 ⊆ 𝐏𝐒𝐏𝐀𝐂𝐄 • 𝐏 ⊆ 𝑩𝑷𝑷 ⊆ 𝑩𝑸𝑷 ⊆ 𝐏𝐒𝐏𝐀𝐂𝐄 𝐏 = 𝐁𝐏𝐏 𝑩𝑸𝑷 𝐍𝐏 Conjecture: 𝑷𝑺𝑷𝑨𝑪𝑬

QC are not all-powerful Quantum computers cannot solve the halting problem Quantum computers are believed not able to solve NP problems efficiently Quantum computers cannot break all crypto systems Quantum computation is NOT parallel computation We are only quantum computer scientists
QC are not all-powerful • Quantum computers cannot solve the halting problem • Quantum computers are believed not able to solve NP problems efficiently • Quantum computers cannot break all crypto systems • Quantum computation is NOT parallel computation • We are only quantum computer scientists