2、圆形电流轴线上的磁场 B 解:“dB在垂直于由di和下组成的平面上。 .dB在由rx组成的平面内,并且和下垂直。 dB= dl sin π Bol dl 2 4元 4元r 由于对称性 B.=∫dB.=0 21 首页上页下页退出
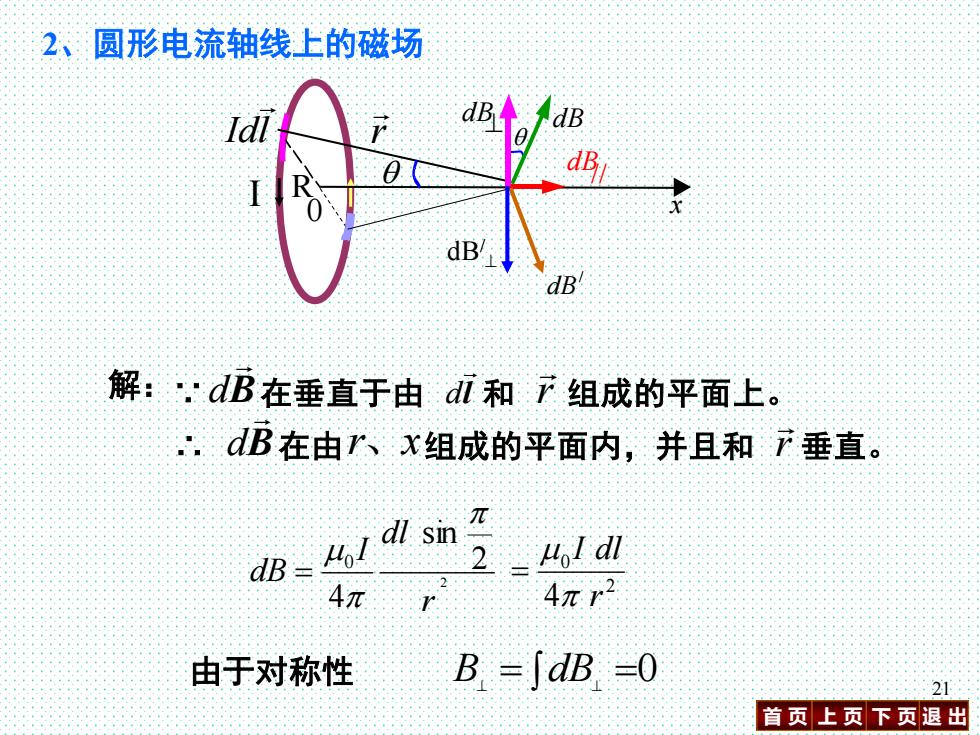
首 页 上 页 下 页 退 出 21 2、圆形电流轴线上的磁场 2 2 sin 4 0 r dl I dB = 解: ∵ B d 在垂直于由 l d 和 r 组成的平面上。 ∴ B d 在 由r、x组成的平面内,并且和 r 垂直。 2 0 4 r I dl = I R 0 x ^ dB // dB q dB q r Idl / dB dB/ ^ 由于对称性 B^ = dB^ =0

所以 B-B-「dB.sin0 2πR -m0 2元R HoIR oIR2 4πr3 d- 2πR 2r3 4oIR2 2(R2+x)为 即 B= R21 (R+x23)3 2 22 首页上页下页退出
首 页 上 页 下 页 退 出 22 3 2 0 2 3 0 4 2r IR dl r IR R = = 2 3 2 2 2 0 ( ) 2 R x R I B + = q sin 4 2 2 0 = R r I dl dl r R r I R = 2 2 0 4 2 3 2 2 2 0 2(R x ) IR + = = = R B Bx dB q 2 所以 sin 即

轴线上任—点P的磁场 B=4R1 2(R2+x2) 圆电流中心的磁场 B= 最 圆电流的中心的 B=141 22R 1/n圆电流的中心的 B=14%l n 2R 23 首页上页下页退出
首 页 上 页 下 页 退 出 23 轴线上任一点P的磁场 2 3 2 2 2 0 ( ) 2 R x R I B + = 圆电流中心的磁场 R I B 2 0 = ½ 圆电流的中心的 R I B 2 2 1 0 = 1/n 圆电流的中心的 R I n B 2 1 0 =

3、载流直螺线管内部的磁场 均匀地绕在圆柱面上的螺旋线圈 称为螺线管.设螺线管的半径为R, 006000分 总长度为L,单位长度内的匝数 a)载直流螺线管 为n.若线圈用细导线绕得很密, c000000000000000000000000000000000000000 则每匝线圈可视为圆形线圈.下 dB 面计算此螺线管轴线上任一场点 88888888888888 8888888888 8888888888 P的磁感应强度B. dl ()直螺线管轴上各点磁感应强度的计算 在距P点I处取一小段dI,则该小段上有ndl匝线圈,对点P而言, 这一小段上的线圈等效于电流强度为lnd的一个圆形电流.该 圆形电流在P点所产生的磁感应强度dB的大小为 dB=Mo R2Indl 2(R2+12) 方向与圆电流构成右手螺旋关系! 24 首页上页下页退出
首 页 上 页 下 页 退 出 24 3、载流直螺线管内部的磁场 均匀地绕在圆柱面上的螺旋线圈 称为螺线管.设螺线管的半径为R, 总长度为L,单位长度内的匝数 为n.若线圈用细导线绕得很密, 则每匝线圈可视为圆形线圈.下 面计算此螺线管轴线上任一场点 P的磁感应强度B. 在距P点l处取一小段dl,则该小段上有ndl匝线圈,对点P而言, 这一小段上的线圈等效于电流强度为Indl的一个圆形电流.该 圆形电流在P点所产生的磁感应强度dB的大小为 2 0 3 2 2 2 2 ( ) R Indl dB R l = + 方向与圆电流构成右手螺旋关系

整个载流螺线管在P点所产生的磁感应强度B的大小为 B-a-可片 R2Indl 设螺线管轴线与从P点到d1处所引矢径r之间的夹角为B,则 1=Rcot B dl =-Rcsc2 BdB ·R2+12=r2 sin'BR 即R2+P=R c p sin2B 、n-货得广t台nn-号aAm 25 首页上页下页退出
首 页 上 页 下 页 退 出 25 l R = cot 整个载流螺线管在P点所产生的磁感应强度B的大小为 2 0 3 2 2 2 2 ( ) R Indl B dB R l = = + 设螺线管轴线与从P点到dl处所引矢径r之间的夹角为β,则 2 dl R d = − csc 2 2 2 2 2 2 sin R R l r r + = = 2 2 2 2 2 2 csc sin R R l R 即 + = = 2 1 2 0 0 0 3 2 1 2 2 2 ( sin ) (cos cos ) 2 2 2 ( ) R Indl B nI d nI R l = = − = − +