
9.1.4磁场中的高斯定理 由于磁力线是无头无尾的闭合曲线,所以穿过任意闭合曲面 的总磁通量必为零。 B.ds=0 这说明)磁力线是无头无尾的闭合曲线, 1))磁场是无源场,磁场无磁单极存在。 首页上页下页退出
首 页 上 页 下 页 退 出 11 9.1.4 磁场中的高斯定理 s B ds 0 这说明 i)磁力线是无头无尾的闭合曲线, ii)磁场是无源场,磁场无磁单极存在。 由于磁力线是无头无尾的闭合曲线,所以穿过任意闭合曲面 的总磁通量必为零

9.1.5毕臭-萨伐尔定律 若磁场中,电流元d到某点P的矢径为下, 则电流元在P点产生的磁感应强度dB的大小与Idl 成正比,与1d经过小于180的角转到矢径下的 方向角的正弦成正比,与的平方成反比,其方 向为d而×r的方向。 Idlsin(di,f) dB=k r2 1)电流元的方向:为线段中 电流的方向。 12 首页上页下页退出
首 页 上 页 下 页 退 出 12 ( ) 2 Idl Idl r sin , dB k r = 1)电流元的方向:为线段中 电流的方向。 I Idl dB r q P 9.1.5 毕奥-萨伐尔定律 若磁场中,电流元 到某点P的矢径为 , 则电流元在P点产生的磁感应强度 的大小与 成正比,与 经过小于 的角转到矢径 的 方向角的正弦成正比,与 的平方成反比,其方 向为 的方向。 Idl r dB Idl Idl 180 Idl r r r
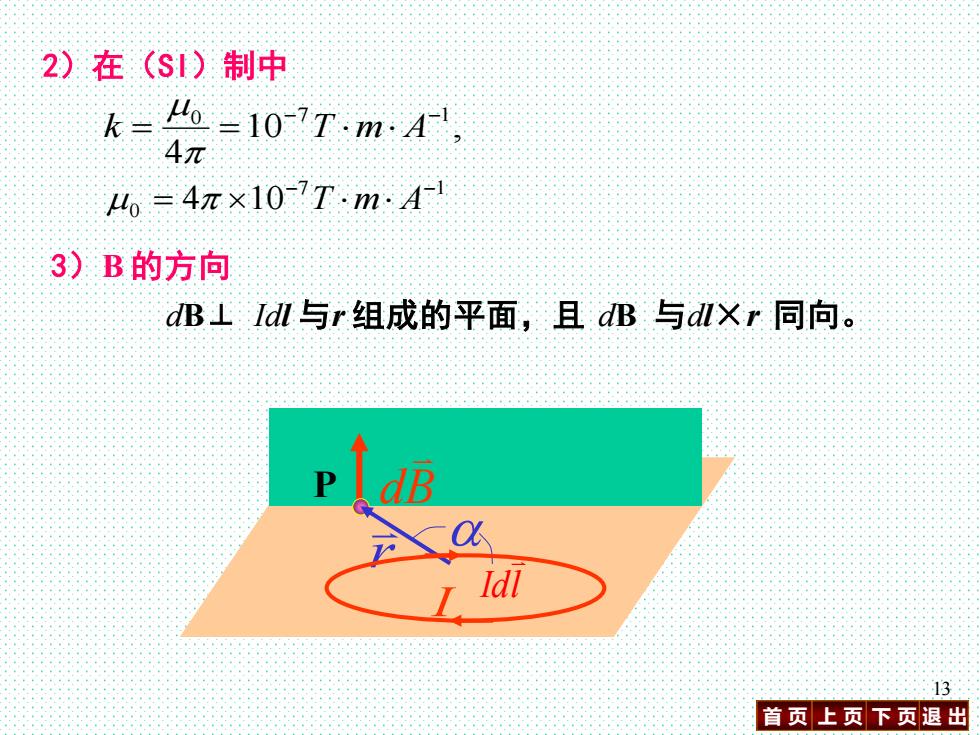
2)在(SI)制中 k==10-1Tm:A, 4元 4=4π×10-7T-m.A 3)B的方向 dB⊥Idl与r组成的平面,且dB与dlXr同向。 P dB Idl 13 首页上页下页退出
首 页 上 页 下 页 退 出 13 2)在(SI)制中 10 , 4 0 −7 −1 k = = T m A 7 1 0 4 10− − = T m A 3)B 的方向 dB⊥ Idl 与r 组成的平面,且 dB 与dl×r 同向。 dB P r Idl I

电流元在P点产生的磁感应强度的矢量式为 dB=。ldlx 4元 3 整个载流导体在P点的磁感应强度则是电流元在P点产生 的dB之矢量和 B-a6-a 14 首页上页下页退出
首 页 上 页 下 页 退 出 14 整个载流导体在P点的磁感应强度则是电流元在P点产生 的 dB 之矢量和 0 3 L L 4 Idl r B dB r = = 0 3 4 Idl r dB r = 电流元在P点产生的磁感应强度的矢量式为

9.1.6毕奥-萨伐尔定律的应用 由Idl Xr确定电流元在P点的dB的方向 将dB向选定的坐标轴投影,然后分别求出 B,-∫B,B,=∫aB, B=∫d 首页上页下页退出
首 页 上 页 下 页 退 出 15 ❖ 由Idl×r 确定电流元在 P点的 dB 的方向 ❖ 将 d B 向选定的坐标轴投影,然后分别求出 x = x B dB y = y B dB = z B dB z 9.1.6 毕奥-萨伐尔定律的应用