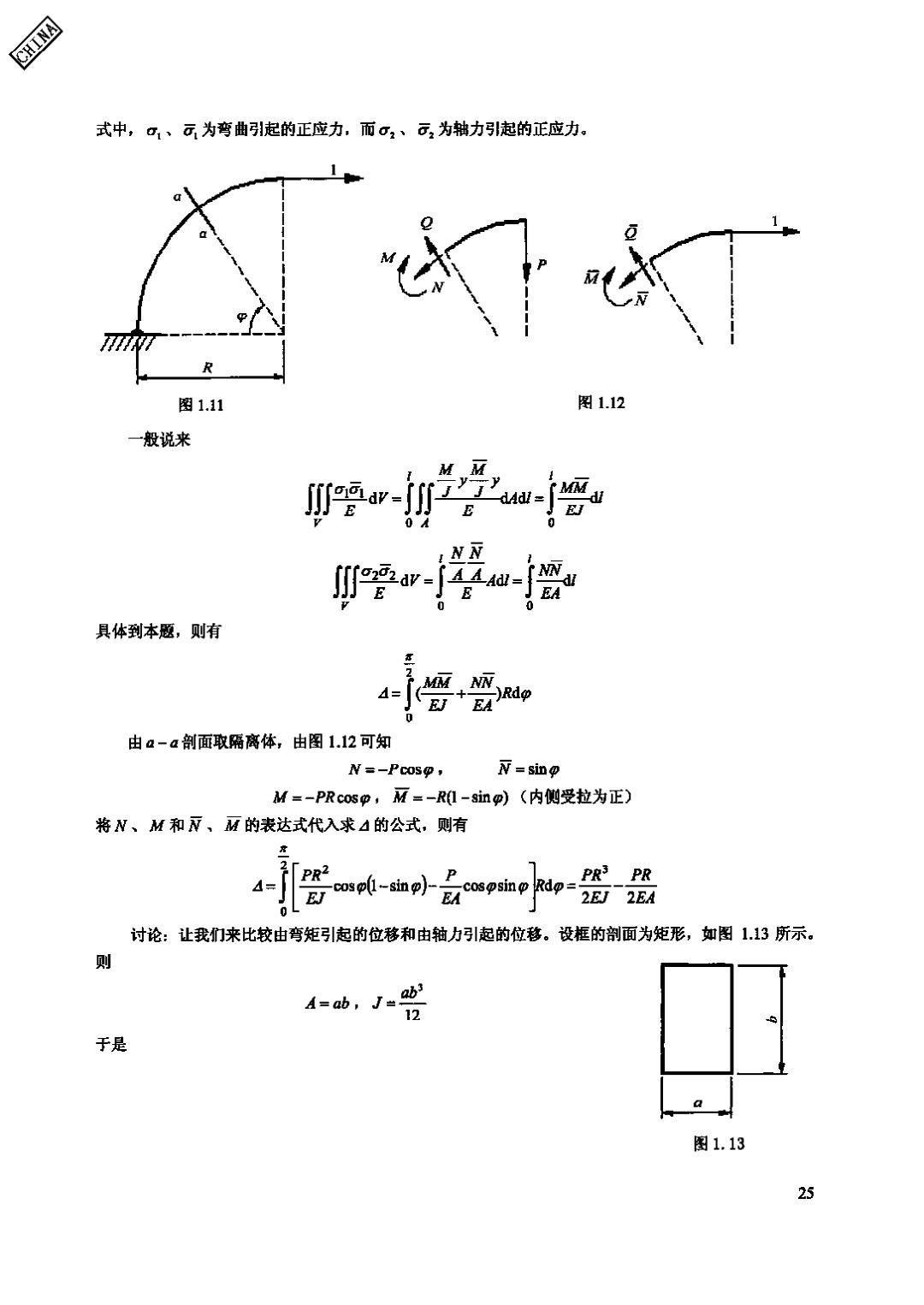
CHINA 式中,口、元为弯曲引起的正应力,而σ2、可2为轴力引起的正应力。 R 图1.11 图1.12 一般说来 I NN 具体到本题,则有 4= ,w + )Rdo EA 0 由a-a剖面取隔离体,由图1.12可知 N=-Pcos, N=sino M=-PRcosp,=-R-inp)(内侧受拉为正) 将W、M和N、M的表达式代入求4的公式,则有 PR3 PR 2EJ 2EA 讨论:让我们来比较由弯矩引起的位移和由轴力引起的位移。设框的剖面为矩形,如图113所示。 则 A=ab,J= 12 于是 a 图1.13 25

CHINA PR 4=2 方2 12R2 3e6 12 由于五较R小得多,故知4比4小得多,因此,有时除将Q的影响忽略之外,还忽路N的影响。这 里要根据具体题日来判断,有一定技巧。 例题15用最小余应变能原理求如图1.14所示梁的弯矩。已知等截面梁一端固持,一端简支,受 到x=0.6L处集中力P的作用,梁截面抗弯刚度为E1。 得:将简支处的约束解除,并以支反力R代替,知图所示。只要知道R的值,梁任意截面处的弯矩 M就可以用下式求出(弯矩以梁的上部受压为正) M1=Px-0.6)+R(1-x),0sx≤0.6L M2=R(化-x), 0.6L≤x≤L 梁的余应变能U为 0.6L 图1.14 .6L >19 M -dx+ 2.E 2 E 0.6L 梁的外力余能为零。 取支反力R作为变分量,根据最小余应变能原理,真实的支反力R应使余应变能”取最小值,其 必要条件为U对支反力R的一次变分等于零,即 0.6L 2d此=0 0.6L 由于变分法则和微分法则基本相同,上式可以变换为 高了Ma+jw 06L OMzdxSR-0 aR 0.6 26
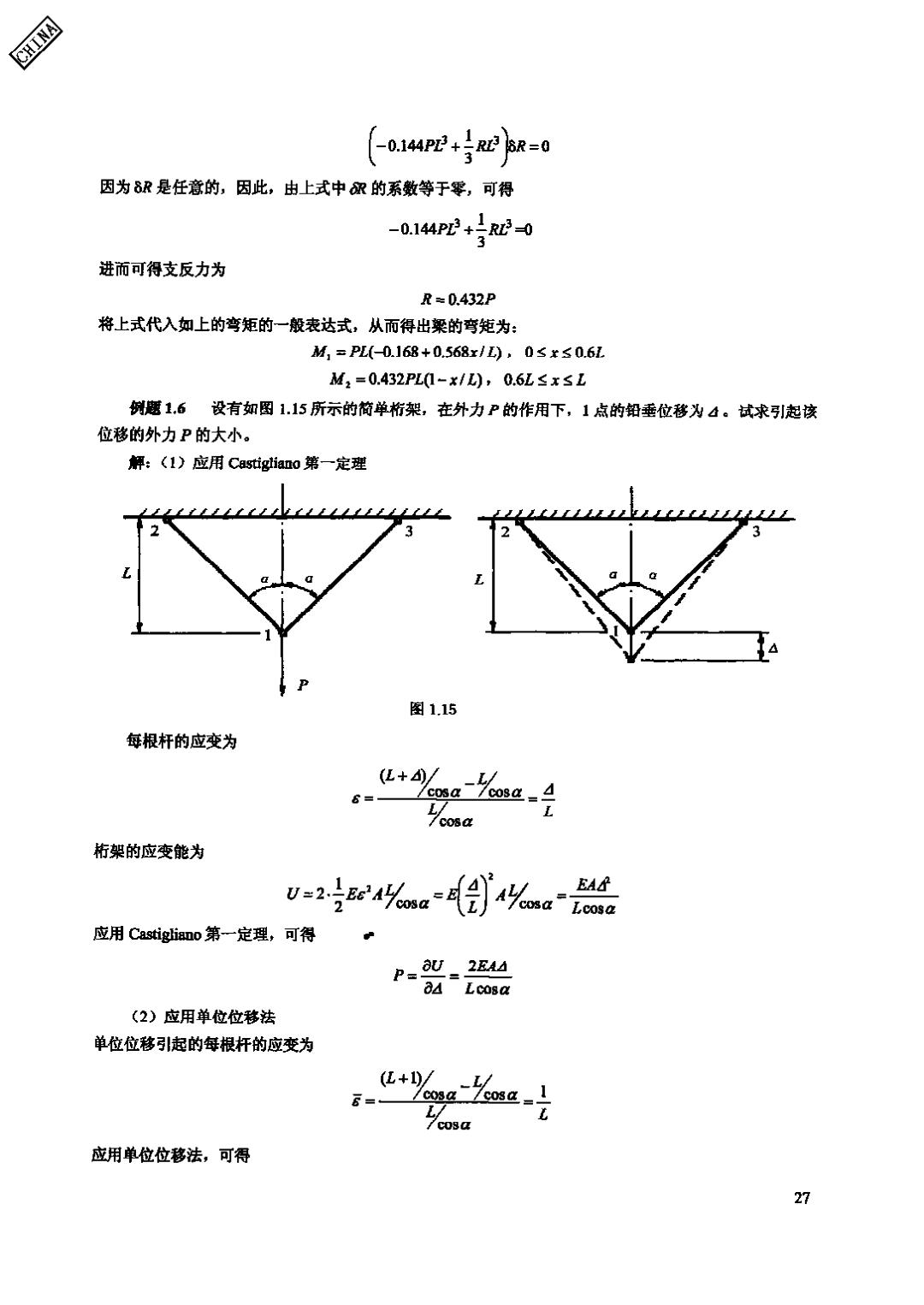
CHINA 【-oi4pE+a=0 因为8R是任意的,因此,由上式中的系数等于零,可得 -0.144Pz2+1R2-0 进而可得支反力为 R=0.432P 将上式代入如上的弯矩的一般表达式,从而得出梁的弯矩为: M1-=PL(-0.168+0.568x1),05x≤0.6L M2=0.432PL1-x1),0.6L≤x≤L 例愿1.6设有如图1.15所示的简单桁架,在外力P的作用下,1点的铅垂位移为4。试求引起该 位移的外力P的大小。 解:(1)应用Castigliano第一定理 图1.15 每根杆的应变为 (L+)/ 6=/cosa /cosa=d L/ /c08a 桁架的应变能为 U=26a以oa=4{ %。 EAd Lcosa 应用Castiglian0第一定理,可得 P=0.2E4 84 Lcosa (2)应用单位位移法 单位位移引起的每根杆的应变为 (L+10/ L/ 6=- L/ /cosa 应用单位位移法,可得 27

CHINA P-2s以a-2是以a-2会 可见,两种方法得到相同的结果。 1.5Ritz方法 我们知道,将最小势能原理的泛函取驻值,可以导出一组适定的徽分方程组,应用 这个微分方程组,可以求力学问题的精确解。当求精确解很困难或暂时不可能时,可以 应用R也方法求力学问题的近似解。 R也方法的要点是假设(选取)一个满足位移边界条件的近似容许函数,该函数中 包含n个待定参数4:,从而使最小势能原理的泛函成为n个待定参数的函数。 将泛函I变分,并令6I=0,可得 8=∑28a,-0,i=12…,n (1.5-1) 由δa的任意性,可得 am =0,i=1,2,…n (1.5-2) Dai 方程(1.5-2)式是包含个未知参数a的n元代数方程组,由此代数方程组求出a:, 代入容许函数中,便得到确定的近似解。 以下用简支粱(如图1.16所示)为例说明Rt也方法的梗概。 图1.16 28

CHINA 设容许函数(挠度)为w=4,sin,显然它满足位移边界条件MO)=0、 0=0、90、=0 应变能函数为 s通rn (1.5-3) 外力势能为 y=-Pa (1.54) 总势能为 H=U+V-Rd-Pay 43 (1.5-5) 将I变分,并令δI=0,可得 边-m 234-P)841=0 (1.5-6) 由δa,的任意性,出上式可得代数方程 TEJ 294-P=0 (1.5-7) 解得 92p (1.5-8)) πEJ 故得问题的近似解 W=_ F 工其 -sin (1.5-9) TE 综上所述,R亿方法将求解微分方程的问题化为解代数方程的问题,便于运用电子数 字计算机进行计算。如果把泛函的积分域划分为有限个子域,则为容许函数的选取带来 很大方便,然后再按R位法的思路求问题的近似解,这便是有限元素法。 29