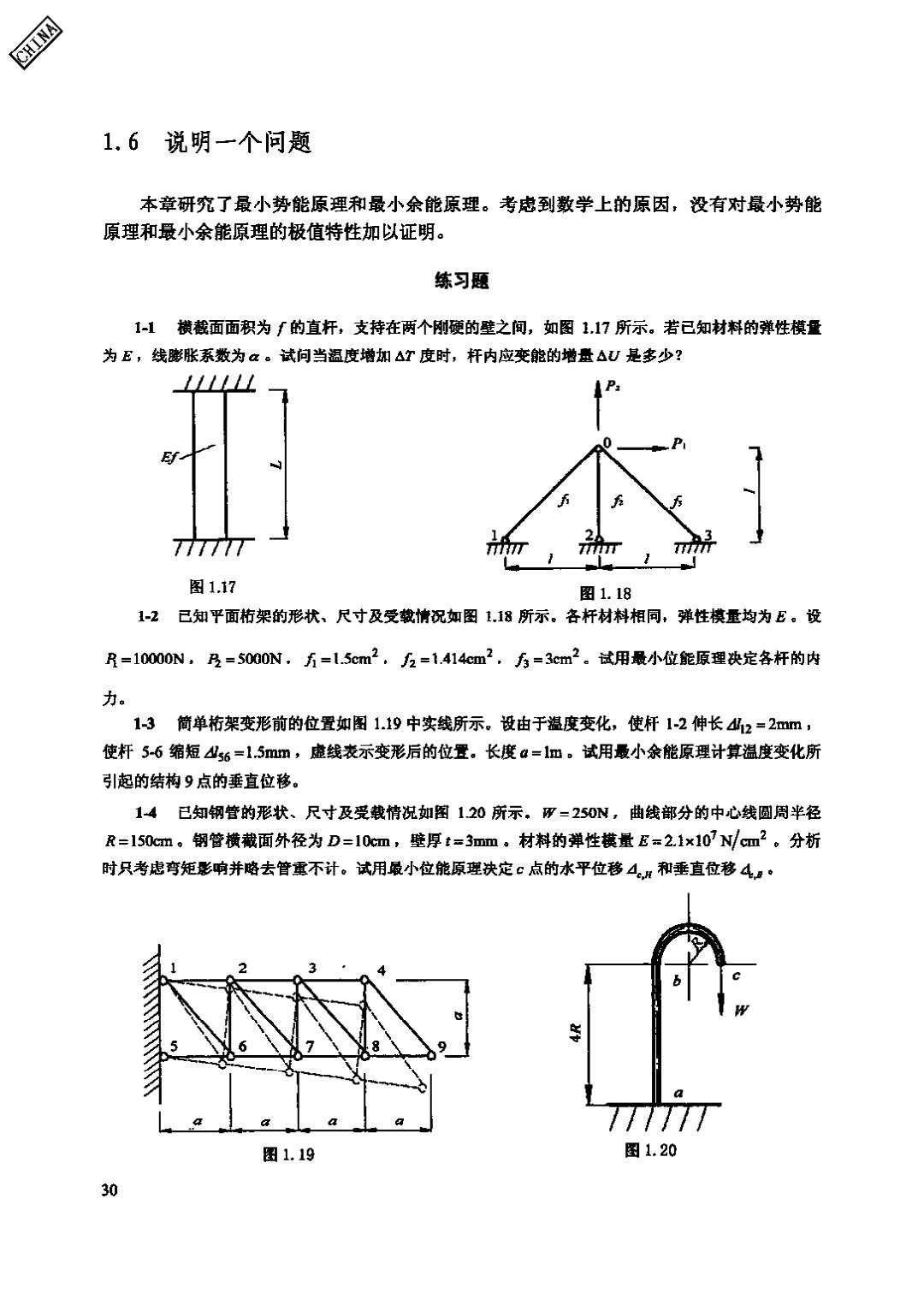
CHINA 1.6说明一个问题 本章研究了最小势能原理和最小余能原理。考虑到数学上的原因,没有对最小势能 原理和最小余能原理的极值特性加以证明。 练习题 1-1横截面面积为f的直杆,支持在两个刚硬的壁之间,如图1.17所示。若已知材料的弹性模量 为E,线膨胀系数为a。试问当温度增加△T度时,杆内应变能的增量△U是多少? L1lllI 7777 图1.17 图1.18 1-2已知平面桁架的形状、尺寸及受载情况如图118所示。各杆材料相同,弹性模重均为E。设 R=10000N,乃=5000N,万=l.5cm2.2=1.414cm2,方=3cm2。试用最小位能原理决定各杆的内 力。 1-3简单桁架变形前的位置如图1.19中实线所示。设由于温度变化,使杆1-2伸长2=2mm, 使杆5-6缩短少56=1.5mm,虚线表示变形后的位置。长度a=1m。试用最小余能原理计算温度变化所 引起的结构9点的垂直位移。 14已知钢管的形状、尺寸及受载情况如图1.20所示。W=250N,曲线部分的中心线圆周半径 R=150cm。钢管横截面外径为D=10心m,壁厚t=3mm。材料的弹性模量E=2.1×10Ncm2。分析 时只考虑弯矩影响并略去管重不计。试用最小位能原理决定c点的水平位移4和垂直位移4,· 图1.19 图1.20 30
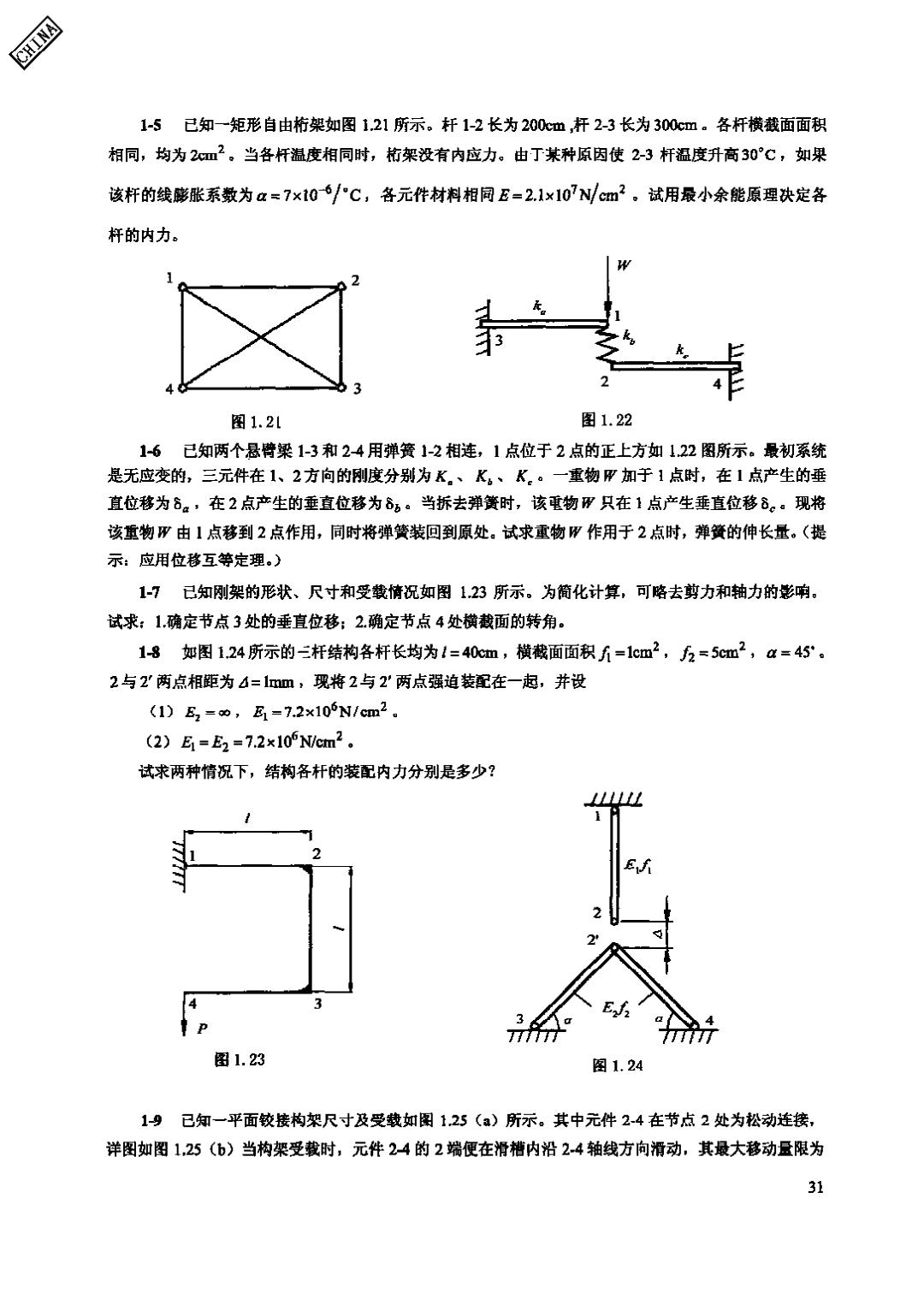
CHINA 1-5已知一矩形自由桁架如图1.21所示。杆1-2长为200心m,杆2-3长为300cm。各杆横截面面积 相同,均为2m。当各杆温度相同时,桁架没有内应力。由丁某种原因使2-3杆温度升高30°℃,如果 该杆的线膨张系数为a=7×106/°C,各元件材料相同E=2.1×107Ncm2。试用最小余能原理决定各 杆的内力。 3 图1.21 图1.22 1-6已知两个悬臂梁1-3和24用弹簧1-2相连,1点位于2点的正上方如1.22图所示。最初系统 是无应变的,三元件在1、2方向的刚度分别为K。、K。、K。。一重物甲加于1点时,在1点产生的垂 直位移为8。,在2点产生的垂直位移为8b。当拆去弹簧时,该重物W只在1点产生垂直位移8。现将 该重物W由1点移到2点作用,同时将弹簧装回到原处。试求重物W作用于2点时,弹簧的伸长量。(提 示:应用位移互等定理。) 1-7已知刚架的形状、尺寸和受载情况如图123所示。为简化计算,可咯去剪力和轴力的彩响。 试求:1确定节点3处的垂直位移:2.确定节点4处横截面的转角。 18如图1.24所示的三杆结构各杆长均为1=40cm,横截面面积斤=1cm2,万=5cm2,,a=45°。 2与2'两点相距为4=1mm,现将2与2'两点强迫装配在一起,并设 (1)E2=∞,E1-7.2×10N1cm2。 (2)E=E2=7.2x105Ncm2. 试求两种情况下,结构各杆的装配内力分别是多少? E. 图1.23 图1.24 19已知一平面较接构架尺寸及受载如图125(a)所示。其中元件24在节点2处为松动连接, 洋图如图1,25(b)当构架受载时,元件24的2端便在滑槽内沿2-4轴线方向滑动,其最大移动量限为 31
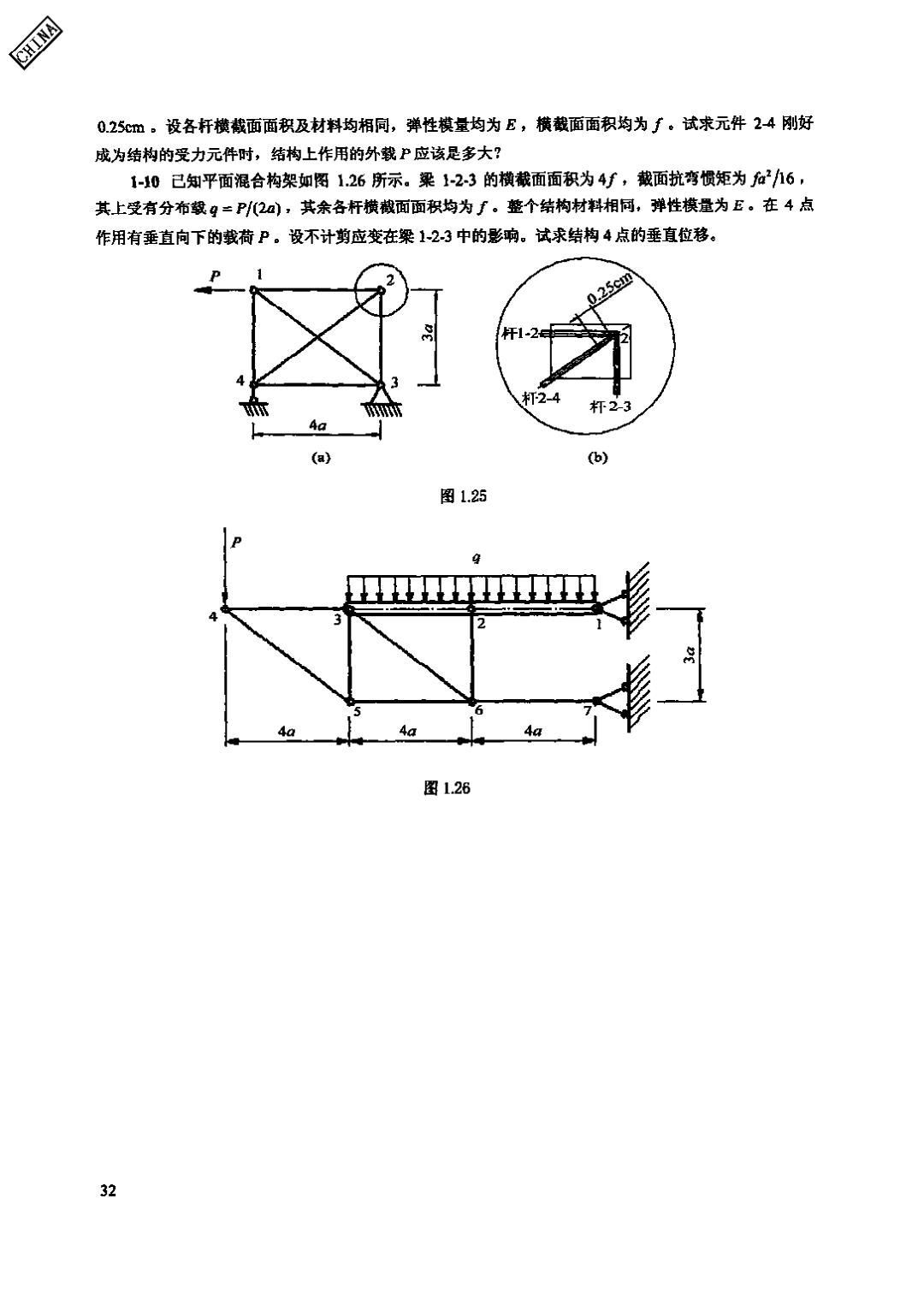
CHINA 0.25Cm。设各杆横截面面积及材料均相同,弹性模量均为E,横截面面积均为手。试求元件24刚好 成为结构的受力元件时,结构上作用的外载P应该是多大? 1【-10已知平面混合构架如图1.26所示。梁1-23的横截面面积为4f,截面抗弯惯矩为a2h6, 其上受有分布载9二P2),其余各杆横截面面积均为∫。整个结构材料相同,弹性模量为E。在4点 作用有垂直向下的载荷P。设不计剪应变在梁123中的影响。试求结构4点的垂直位移。 25cm 杆1-2 杆23 Aa (a) (b) 图1.25 4a 图1.26 32

CHINA 第2章 力法 2.1引言 飞行器结构力学中存在两类基本量一力类量和位移类量;飞行器结构力学中存在 三类基本关系一力类量之间的平衡关系、位移类量之间的协调关系、力类量和位移类 量之间的物理关系(物理关系又称本构关系)。本章我们以力为基本变量来分析结构,称 之为力法。下一章将以位移为基本变量来分折结构,称之为位移法。可以推知,如果以 力和位移两类变量为基本变量来分析结构,则可称之为混合法。在力法一章中,我们将 研究静定结构的内力和位移计算,重点研究静不定结构的内力和位移计算,内容包括一 般力法、矩阵力法和秩力法。 为了研究问题的方便,本节概略地研究结构的组成和静不定度的判定问题。 2.1.1系统的几何不变性 飞行器结构是指飞行器的受力系统。为了承受载荷,受力结构各元件之间不应发生 相对的刚体移动,以保持结构原来的几何形状。结构在载荷作用下保持其几何形状不可 改变的特性,称为结构的几何不变性。因为组成结构的元件不是绝对刚性的,在载荷作 用下各个元件都将发生微小的弹性变形。所以,要求结构的几何形状绝对不变是不可能 的,也是不必要的。因此,几何不变性是指:当不考虑弹性变形时,结构保持其几何形状 不变的特性。一个系统在载荷作用下,按照其几何形状的可变性分为以下三种类型。 (1)几何可变系统 系统受载后,在元件不产生弹性变形的情祝下,其儿何形状就发生了显著的改变。 这种系统称为几何可变系统,在机械原理中,称之为“机构”,显然,它不能作为结构 来利用。例如图2.1所示就是一种几何可变系统。它是由三根杆子铰接组成的,杆子1-2及 34的一端又铰接在基础上。当有较小的外载P作用时,该系统的几何形状可能发生较大 9m97 图2.1 33

CHINA 的变化,变化的一个位形如图中虚线所示。这时的变形并不引起杆子的弹牲变形。因而, 杆子也不会产生与外载P平衡的内力。在这种情况下,只要没有其它阻碍,系统的形状 就将继续地变化下去,直到倒伏在基础上为止。显然,几何可变系统在不产生弹性变形 的情况下,其元件之间就能发生相对的刚体位移。因而,在结构设计时,必须避免这种 情况。 (2)几何不变系统 这种系统在受载后,由于各元件之间互相牵连,将引起有关元件的弹性变形,其儿 何形状将产生微小的变化。从而,产生一定的内力与外载荷相平衡,阻止了系统的几何 形状继续改变。由于系统变形是微小的,在工程中就称其为几何不变系统。这种系统能 够承受任意方向与不同形式的外载荷,是结构力学的研究对象。这种受力系统称为结构。 例如图2.2就是一个几何不变系统,它是在图2.1的系统上,用一根杆子把结点1和3连接而 成。当外力P作用在系统上时,由于杆子13的作用,系统不能任意改变其几何形状。这 时,系统在P力作用下,变成图2.2中虚线所示的形状,系统中的杆子13,2-3和34都有 弹性变形,因而,引起的内力与外载荷P相平衡。这时的系统也发生变形,但这种变形 由于受到元件刚性的限制,通常是微小的,不影响系统的正常使用。如果所有元件都是 绝对刚硬的,系统就不会有任何形状的改变。显然,几何不变系统受力时,在不考虑弹 性变形的情况下,其各元件之间并不会发生相对的刚体位移。因而,能保持源有的几何形状。 7777777777 777 777777777777777 图2.2 图2.3 (3)瞬时几何可变系统 这种系统介于以上两种系统之间,在受载后,先是发生比较明显的几何变形,而后 由于变形引起了系统内部各元件的相互限制,使形状不能继续变下去。所以它在开始受 力的“瞬时”是几何可变的。这种系统往往是由于元件安排得不合理而造成的。例如图23 就是一种典型的瞬时可变系统(简称为瞬变系统)。它是在图2.1的系统上加一杆2-5所形 成的。 当有外载P作用时,由于1-2、2-5杆均与力P相垂直,故其不能阻碍结点沿水平线2 3方向的移动。所以在开始加力的瞬间,系统是几何可变的。但当系统有显著的变形以后(如 虚线),就使杆1-2和杆25明显的伸长,因此也就产生了阻止其继续变形的能力,使它不 能像图2.1那样继续变下去。所以,瞬变系统的几何形状也是不能任意改变的,在这一点 34