
CHINA 令={6}表示单位位移引起的应变,上式变换为 84, ae))av (1.4-19) 比较(1.4-19)和(1.417)式可见,如果考虑到本构关系,两个公式是相同的。因 此,在一定意义上说,单位位移法就是Castigliano第一定理的一种应用。 (2)单位载荷法及其与Castigliano第二定理的关系 某些著作中,这样论述单位载荷法:为了确定弹性结构中某处某方向的广义位移4, 施加一个与该广义位移对应的广义虚力δ2。由于外力余虚功等于余虚应变能,故有 480-Iff(6,80,+e,8o,+6.80.+8+8+y..8F)dv (14-20) 由于62与80,6gy,δ0,δx,8t,8xx之间仅需要满足平衡条件和力学边界条件, 做可以认为它们之间成比例,可得 480,=0je,8a.+6,80,+e,8a,+7,8元,+y.8:+.8f.8,dr(1.4-21) 式中,8可,8可,6ā2,δ元,8元,8Fx为单位广义虚力引起的虚应力。 由等号两边约去δ2,可得 4=∬(6.8可,+6,8可,+,8可:+yw87,+y8元。+y8.)a" (1.4-22) 这就是单位载荷法的计算公式。它表示:为了确定弹性结构中某处某方向的广义位移4, 只要施加一个与该广义位移相应的单位广义力,则由实际载荷和单位载荷引起的余应变 能U°在数值上就等于该单位力对应的广义位移。 以下讨论单位载荷法与Castigliano第二定理的关系。 由Castigliano第二定理可得 0-是t-jyr (1.4-23) 20
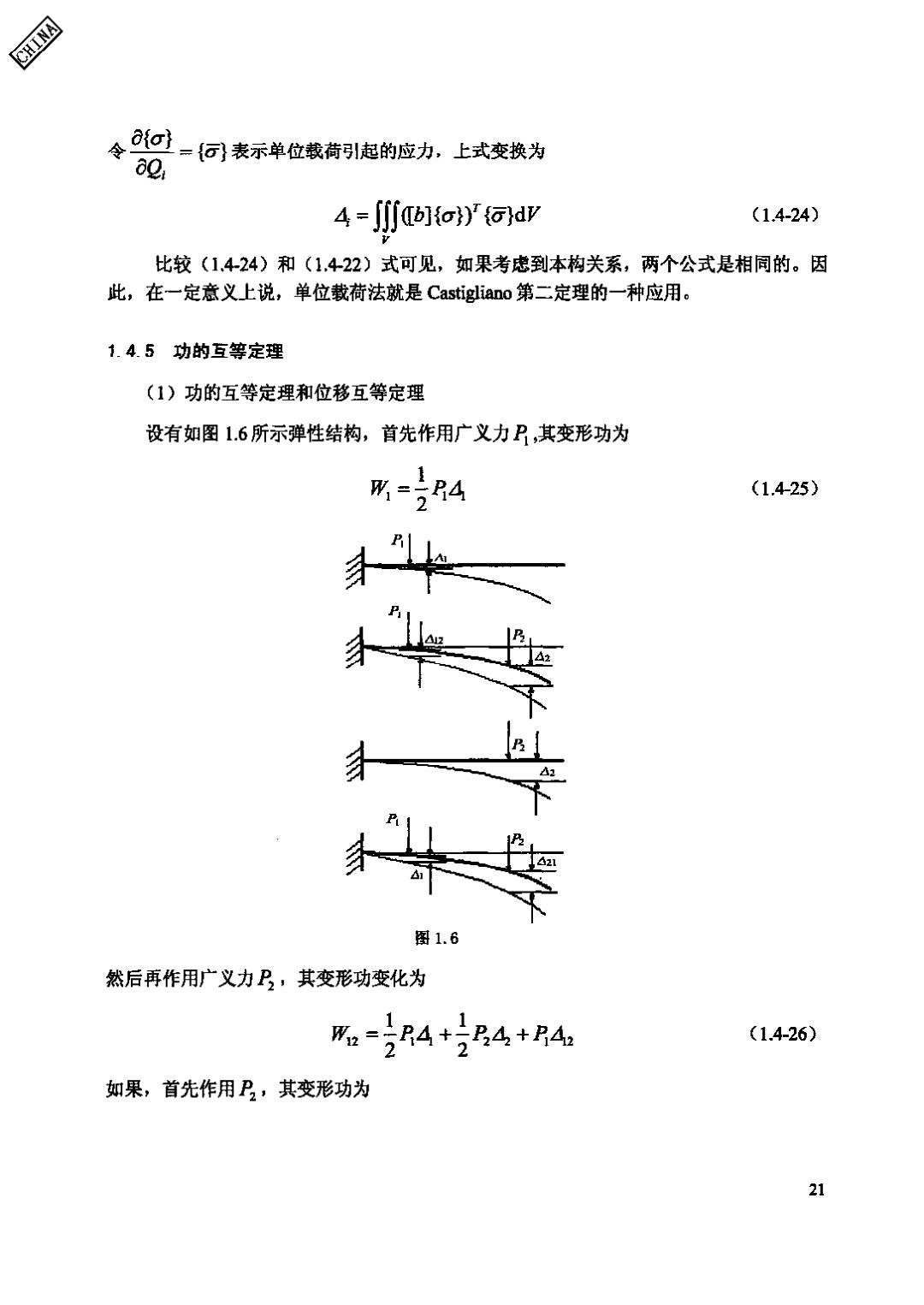
CHINA 令0}-{何表示单位载荷引起的应力,上式变换为 82 4=j∬]oy@dv (1.4-24) 比较(1.424)和(1.422)式可见,如果考虑到本构关系,两个公式是相同的。因 此,在一定意义上说,单位载荷法就是Castigliano第二定理的一种应用。 1.4.5功的互等定理 (1)功的互等定理和位移互等定理 设有如图1.6所示弹性结构,首先作用广义力P,其变形功为 所4 (1.4-25) 图1.6 然后再作用广义力P,其变形功变化为 m4+4+R4 (1.4-26) 2 如果,首先作用P,其变形功为 21

CHINA W2= 4 (1.4-27) 然后再作用P,则其变形功变化为 m=B4+2R4+B4 1 (1.4-28) 2 因为系统是保守的,变形功与力的作用次序无关,故有 形z=W 从而可得 R42=P2421 (1.4-29) 这就是功的互等定理的一种表示形式。 如果取=P2,则有42=山21,如果取R=2=1,则将之写为可2=621,推广 到一般情况则为 8y=8m (1.4-30) 这就是位移互等定理。 (2)功的互等定理和力的互等定理 设有如图1.7所示两端固支的杆。首先作用广义位移4,其变形功为 所4w (1.4-31) 两子 图1.7 22

CHINA 然后再作用广义位移△,,其变形功为 1 形a=24W+24W,+4N: (1.4-32) 如果首先作用广义位移4,其变形功 1 -24 (1.4-33) 然后再作用广义位移4,其变形能为 1 1=24N,+24N+N4 (1.4-34) 设系统的线性弹性体,变形功与力的作用次序无关,故有 W2=W1 即 4N+4,+4a=方4+4g+4 (1.435) 故有 42N21=4N2 (1.4-36) 这便是功的互等定理的另一种表示形式。 如果取4=42,则有N2=N21。如果取4=42=1,则将之写为2=721,推广 到一般情况则为 可二T拉 (1.4-37) 这就是力的互等定理。 1.4.6叠加原理 结构力学中研究的线性弹性系统,叠加原理适用,也可以说,在小位移假设下,叠 加原理成立(注:课程中有非线性内容,叠加原理不适用)。 例题1.4 设有如图18的二圆环,在P作用下平衡,设其弯曲剖面刚度系数为以,拉压剖面刚 度系数为EA。试求杆端水平位移A。 23
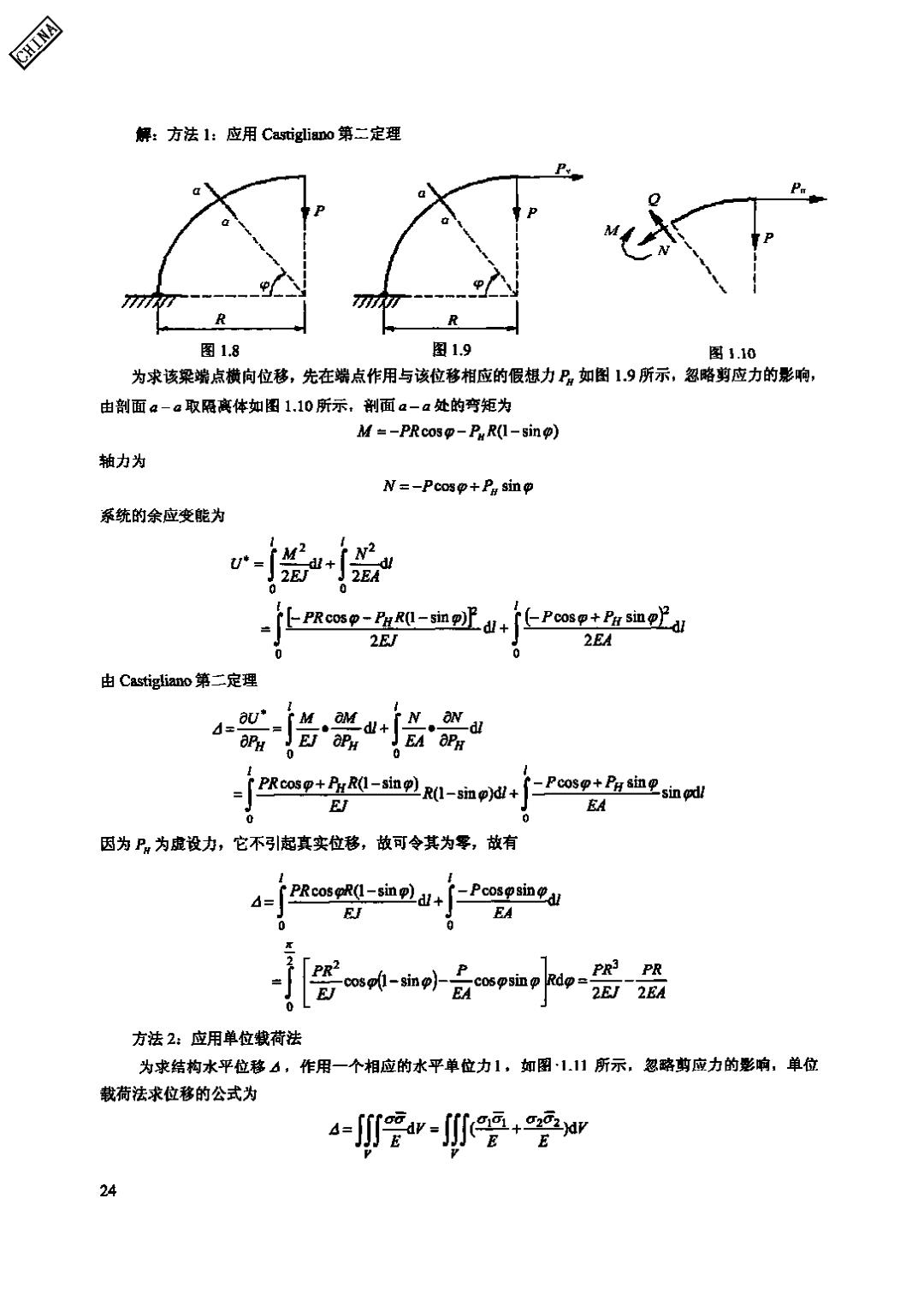
CHINA 解:方法1:应用Castigliano第二定理 图1.8 图1.9 图1.10 为求该梁端点横向位移,先在端点作用与该位移相应的假想力P如图1.9所示,忽略剪应力的影响, 由剖面4-a取隔离体如图1.10所示,剖面a一a处的弯矩为 M=-PRcoso-P R(1-sin) 轴力为 N=-Pcoso+P sin 系统的余应变能为 广版2 2+ 0 --R0-sin+长Posp+as血此 2E/ 2EA 由Castigliano第二定理 8U* d M,aMd出+ OPH EJ aPH PRcosp+PR(1-sin)R(1-si)di+ ,-Pcosp+PHsi恤见5inpd EJ EA 因为P:为虚设力,它不引起真实位移,故可令其为零,故有 PRcosoR(1-sin)dl+ -Pcospsind EA 2EJ 2EA 方法2:应用单位载荷法 为求结构水平位移b,作用一个相应的水平单位力1,如图111所示,忽略剪应力的影响,单位 载荷法求位移的公式为 4-旷管w-要+要w 24