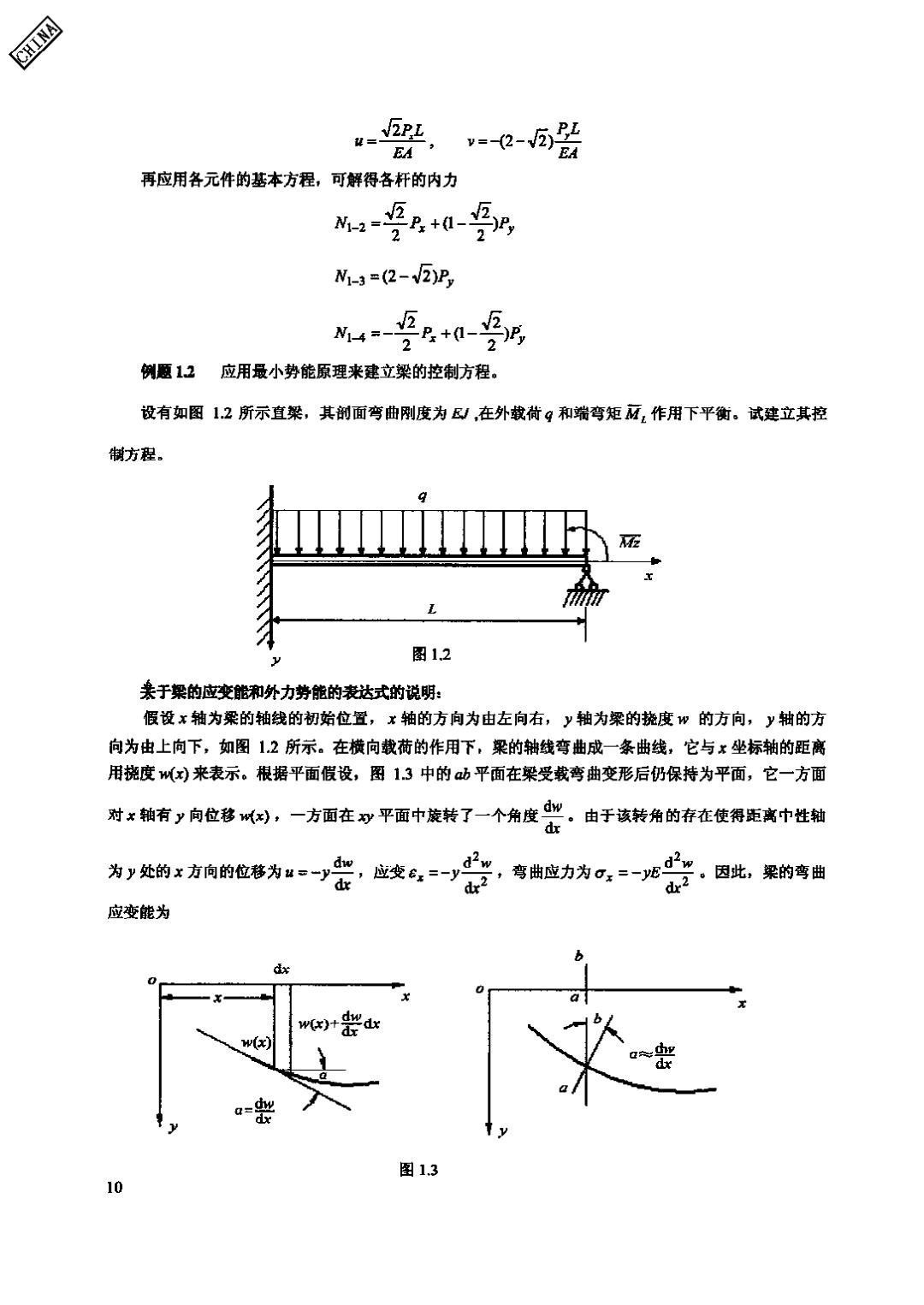
CHINA =2虹 EA =2- EA 再应用各元件的基本方程,可解得各杆的内力 M-2=5B.+0- 2 2 N1-3=(2-V2)P 水4-2 2 例题12 应用最小势能原理来建立梁的控制方程。 设有如图1.2所示直菜,其剖面弯曲刚度为/,在外载荷g和端弯矩M,作用下平衡。试建立其控 制方程。 图12 美于梁的应变能和外力劳能的表达式的说明: 假设x轴为梁的轴线的初始位置,x轴的方向为由左向右,y轴为梁的挠度w的方向,y轴的方 向为由上向下,如图12所示。在横向载荷的作用下,梁的轴线弯曲成一条曲线,它与x坐标轴的距离 用桡度w(x)来表示。根据平面假设,图1.3中的a山平面在梁受载弯曲变形后仍保持为平面,它一方面 :轴有y向位移),一方面在y平面中旋转了一个角度。由于该转角的存在使得距离中 为y处的x方向的位移为u=一y 击,应变=y 弯曲应力为。=-地 因此,梁的弯曲 应变能为 x w(r)+dw dx dw 图1.3 10

CHINA 0-2,.av-0片6a 式中,A为梁的截面面积:J为樂的轴惯矩。 分布载荷g作用在梁的重心线上(并且重心线和弯曲中心线重合),而不是作用在梁的表面,这就 是说wx)是g作用点的位移,并且和g的作用方向相同,因此,由g引起的外力势能为 Va =-wqdx 0 关于弯矩M的方向,这里规定为:能在粱的剖面上y>0的一边产生正的σ,的弯矩,规定为正的弯矩。 另一方面,由图13可见,在x二L处假设的转角的正方向正好与弯矩M的正方向相反,因此,由梁 业 端的弯矩M,产生的外力势能为 Tu-Mt 综上所述,总的外力势能为 解:梁的最小势能原理的泛函为 其边界条件为 wM0=w☑=0, dw=0 dx引x-0 将Ⅱ变分,并令8Ⅱ=0,则有 应用Green定理(进行分部积分) dd do j空 dr2 Jy)δ dx dx =3s dx2 d (3e 、d 。d(3 ?wdr 11

CHINA 故有 r〔3)一☒]δx十2一8C少, 8n= 20|x=z一EJaz8x|x-o d 7d+a48密-=0 应用位移边界条件,可将上式化简为 是-9a咖++,=0 由òw的任意性,并用适当条件保证x=L处8具有任意性,则可得出控制方程 dx 3 2小9s0 Bydiw +所=0 可见这是体域中的平衡方程和力学边界条件。从变分学的角度看问题,这使是Er方程和自然边界条 件。 1.3余虚功原理和最小余能原理 按照广义力和广义位移之间的对应关系,将(1.1-3)和(1.14)乘上相应的虚应力 任意的、微小的、平衡所容许的应力,然后积分,并代数相如,可得 孤e空o,+%, tvou)t 2之8o,+(6,-8c:, +0.0s+0028NΨ Ow Ov (1.3-1) +j[u-a6o,+8r,m+8r2n)+(v-twl+8c,m+8r.)) +(w-w)8xz1+8xm+8o,n)]dS=0 应用Green定理 0:dv a,d=-as+器 (1.3-2a) 暗,-,w- (1.3-2b) 12

CHINA 容a-么a,+项密v (1.3-2c) -密r-s+小-v (1.3-2i) 将(1.3-2a)~(1.3-2i)代入(1.3-1),可得 0e,8o,+,8o,+e.8a,+nt,+78r.+7.8ta+u(a y 内警号警经+w +a)+ax++ u(6o/+8,m+t。小+6:+8o,m+8F网 (1.3-3) +w(8t 1+8tm+8o.n)ls-[u(80l+8tm+8tn) +v(8t1+80,m+8tn)+w(8tl+8tm+80,n)lds =0 考虑到平衡条件和力学边界条件的变分式为 Γ6g+08r2+08g=0 的匹+ 6Tz-0 6cy+ x (1.1-1) 而5a+6z+6c:-0 801+8tm+8tn=0 δt+6oym+8tgn=0 (1.1-2) 8t l+8tm+8o.n-0 将(1.1-1)和(1.1-2)代入(1.3-3),可得 680,+6,8o,+o.80.+y8t+y,8t,+y.8t.lv (6o/+8t,m+8a网+8r.+a,m+8f) (1.34) +w(8t1+8tm+8o,n)]ds =0 13

CHINA 这就是余虚功原理的表达式,它表明:当物体处于变形协调状态时,其内力余虚功等于 外力余虚功。这里我们指出,无论材料的本构关系如何,余虚功原理都成立。 将(134)写成矩阵形式,则有 soav-f(ay Pds-0 (1.34) 将本构关系(1.1-6)代入(1.34),可得 -AYPs (1.3-5) 进而可得 j∬oaar-ayds=0 (1.36) 上式可以处理为一个泛函的驻值问题 r-oar-fayipnas (1.3-7) 其先决条件为(1.1-1)、(1.1-2)式。 泛函T和其先决条件(1.1-1)、(1.1-2)一起构成一个变分原理,这就是最小余能原 理。有时将V=∬片o)圆oV称为内力余能,而格V=-∬4yPs称为外 力余能,则T=U+V称为总余能,8厂=0是总余能取最小值的必要条件。 这里我们指出,有的学者将最小余能原理中的外力余能表示为 r-∬ayar-∬4yP例as 这是不对的,前面的推导过程已经充分说明了这一点: 例题13平面桁架的形状、尺寸如图1,4所示,已知各杆的截面面积均为A,弹性模量均为E。 用最小余能原理分别确定下列情况下桁架中各杆的内力: (1)当24杆比设计尺寸短了么并强迫装配起来。 (2)由于某种原因使2-3杆的温度升高△T,该杆的热膨 胀系数为a。 解:(1)把24杆切断,代以轴力N,由几何关系和平衡 条件可得各杆杆长及内力与轴力N的关系。如表12所示。 则系统的内力余能 14 图1.4桁架结构