
CHINA Ty=Tx (ta =tx 力学边界条件 0l+Tgm+tn-X=0 txl+oym+rn-F=0 (1.1-2) Tal+tm+o.n-Z=0 几何条件 Bu =0 Ov Ey =0 =0 (1.1-3) Ou Yy- 十 1=0 可 一创 a=0 Ya z 0=0 位移边界条件 u-z=0 y-立=0 (1.1-4) w-币=0 本构关系 69 02 06 .: : =0 (1.1-5) as a6s 品品 对各向同性体,为 5
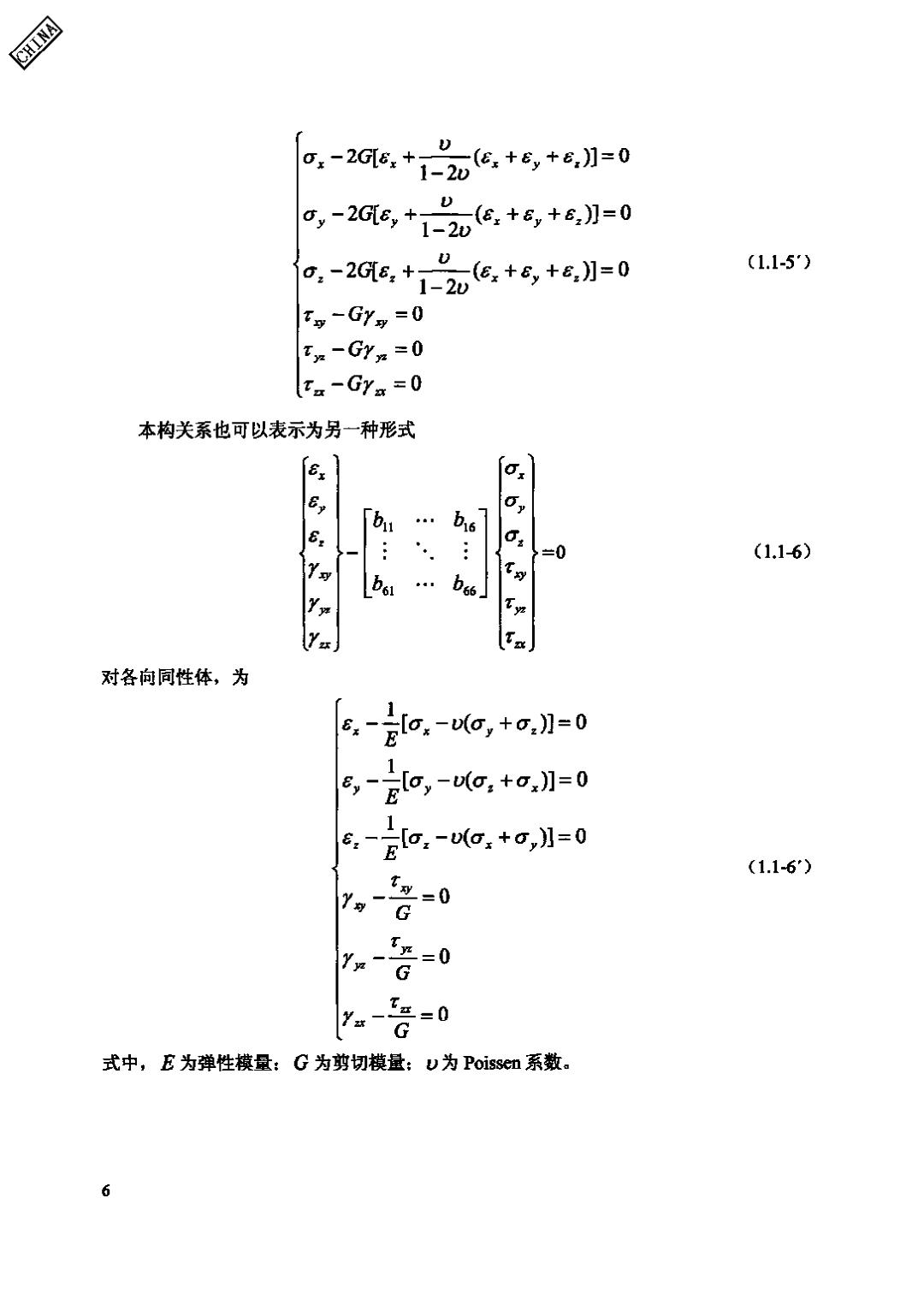
CHINA 。,-2G6.+气”6,+6,+8,1=0 1-2w 口,-20e,+72e+,+e】=0 a,-2G6,+,”6,+6,+8,月=0 (1.1-5) 1-2w Tg-Gysy=0 Tx-GY=0 ta-GY=0 本构关系也可以表示为另一种形式 Ex O, e … b67 0, 兰0 (1.1-6) Y可 bo 6的) \Ya 对各向同性体,为 2a,-g,+o,l=0 1 9,。o,-(o,+o,】=0 6.-o.-a.+,】=0 E (1.1-6) Y ty二0 G G T三=0 式中,E为弹性模量:G为剪切模量:U为Poissen系数

CHINA 1.2虚功原理和最小势能原理 根据广义力和广义位移之间的对应关系,将(1.1-1)、(1.1-2)式乘上相应的虚位移 任意的、微小的、约束所容许的位移,然后积分,并代数相加,可得 +00+e+8w -jig++爱+u+a++a t2.+)wdv+J(C+rn-X8 ++创正 (1.2-1) +(!+o,m+n-Y)8v+(t1+m+o.n-Z)8wkis-0 应用Green定理 -功器a-Laas+加.警r (1.2-2a) 功0adw-夏as+ (1.2-26) ..wdfo. (1.2-2i) +S。 将(12-2a)~(1.2-2i)代入(1.2-1),可得 0Bu十+xOδu_S+(txx ta.ax+9 Ov 0v 2+0,0y M9g+ y u (1.2-3) J(a.u+r,mδ+tan8+(c8vto,mv+Tn5y) +(c.w+t,ymδv+a,nwS-j∬(u+6v+2òwds=0 将(1.1-3)、(1.14)式代入(12-3)式,可得 7

CHINA o.80,+o8c,+0.86.+t8+t,oyn+r.8ya (1.24) -(XOu+Y8v+28w)dv-[f(Xou+Y8v+Z8w)ds=0 这就是虚功原理的表达式,它表明:当弹性体在外力作用下处于平衡状态时,对任意为 约束所容许的虚位移,外力虚功等于内力虚功。这里我们指出,无论材料本构关系如何, 虚功原理都成立。 将(1.24)式写为矩阵形式,则有 tfoy 8-FY 4hdv-[fP)ds=0 (1.24) 式中{o}一一应力列阵:8}—应变的变分列阵;{F}—体力列阵;谷}—位 移的变分列阵;{P一—面力列阵;用T表示矩阵的转置。 将本构关系(1.1-5)代入(1.2-4),可得 Jj∬re[a]e-Fy6a4]av-∬Py84ds=0 (1.2-5) 进而可得 8∬吃a'a]e-Fy41av-aPyt4as=0 (1.2-6) 上式可以处理为一个泛函的驻值问题 a-(FY ta-PYids (1.2-7) 其先决条件为(1.1-3)、(1.14)式 泛函(12-7)和其先决条件(1.1-3)、(1.14)一起构成一个变分原理,这就是最小 势能原理。有时将U=a[o8dr称为内力势能或者应变能,而将 V=-∬F少{47-厂Py4ds称为外力势能,则7=U+r称为总势能。 这里我们指出,6亚=0是总势能取驻值的充分必要条件,但是,仅是总势能取极值 (最小值)的必要条件。 例题11为了说明最小势能原理及其应用,我们来研究如图11所示的桁架。桁架在结点1处受 水平方向和垂直方向的集中力P,和P,的作用,用最小势能原理求结构的水平和垂直位移,并求结构的 内力
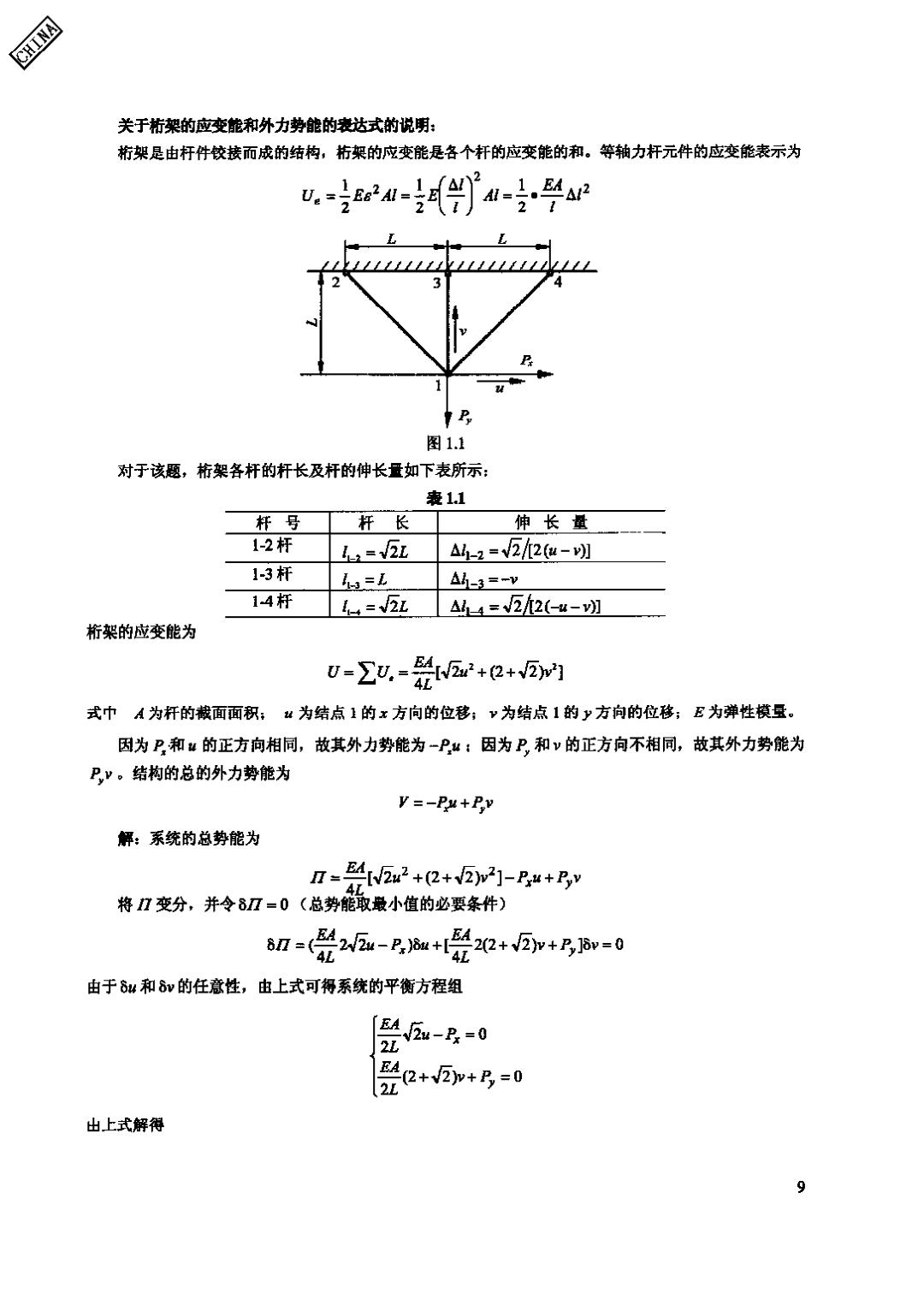
CHINA 关于桁架的应变能和外力势能的表达式的说明: 桁架是由杆件铰接而成的结构,桁架的应变能是各个杆的应交能的和。等轴力杆元件的应变能表示为 12 2 图1.1 对于该题,桁架各杆的杆长及杆的伸长量如下表所示: 表1.1 杆号 杆长 伸长量 1-2杆 =2t A1-2=V22u-叨 13杆 h=L 4h3=-y 14杆 I=2L 4出4=22(-u- 桁架的应变能为 U-.-2++1 式巾A为杆的截面面积:“为结点上的x方向的位移;~为结点1的y方向的位移;E为弹性模量。 因为P和“的正方向相同,故其外力势能为-P“:因为P和v的正方向不相同,故其外力势能为 卫y。结构的总的外力势能为 V=-Pu+Pv 解:系统的总势能为 n=4N2u2+(2+2r2]-P4+,y 将Ⅱ变分,并令8Ⅱ=0(总势能取最小值的必要条件) 8n-(02-2,m+l020+v②p+R,v=0 由于8u和8v的任意性,由上式可得系统的平衡方程组 [42w-R=0 21 2+②加+B=0 EA 出上式解得 9