
8-l-1离散型Hopfield网络 ·相关参数说明 任意神经元泻间的突触权值为”,,神经元之间 连接是对称的,神经元自身无连接 每个神经元都同其他的神经元相连,其输出信号经过 其他神经元又有可能反馈给自己 设Hopfield网络中有n个神经元,其中任意神经元的 输入用,表示,输出V,用表示,它们都是时间的函 数,其中y,(t)也称为神经元在时刻的状态。 y,()=∑w,4,)+b y,(t+1)=f(y,(t) j≠i
8-1-1 离散型Hopfield网络 ◼ 相关参数说明 ❑ 任意神经元 与 间的突触权值为 ,神经元之间 连接是对称的,神经元自身无连接. ❑ 每个神经元都同其他的神经元相连,其输出信号经过 其他神经元又有可能反馈给自己 ❑ 设Hopfield网络中有n个神经元,其中任意神经元的 输入用 表示,输出 用表示,它们都是时间的函 数,其中 也称为神经元在时刻 的状态。 n 1 ( ) ( ) i ij j i j j i v t w u t b = = + ( 1) ( ( )) i i v t f v t + = i j wij i u i v ( ) t i v t

8-l-1离散型Hopfield网络 激励函数 立0+4≥0 j≠1 ,(t+1)= 1 0负<0 j
激励函数 n 1 n 1 1 ( ) 0 ( 1) 1 ( ) 0, ij j i j j i i ij j i j j i w v t b v t w v t b = = + + = − + 8-1-1 离散型Hopfield网络

8-1-2连续型Hopfield网络 连续Hopfield网结构见图(a),是单层反馈非线性网 每一节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现 网络的神经元(节点),见图(b)。 (a)结构示意图 (b) 图9-2连续型Hopfeld网络
8-1-2 连续型Hopfield网络 连续Hopfield网结构见图(a),是单层反馈非线性网, 每一节点的输出反馈至输入。 Hopfield用模拟电路(电阻、电容和运算放大器)实现 网络的神经元(节点),见图(b)。 图9-2 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•)
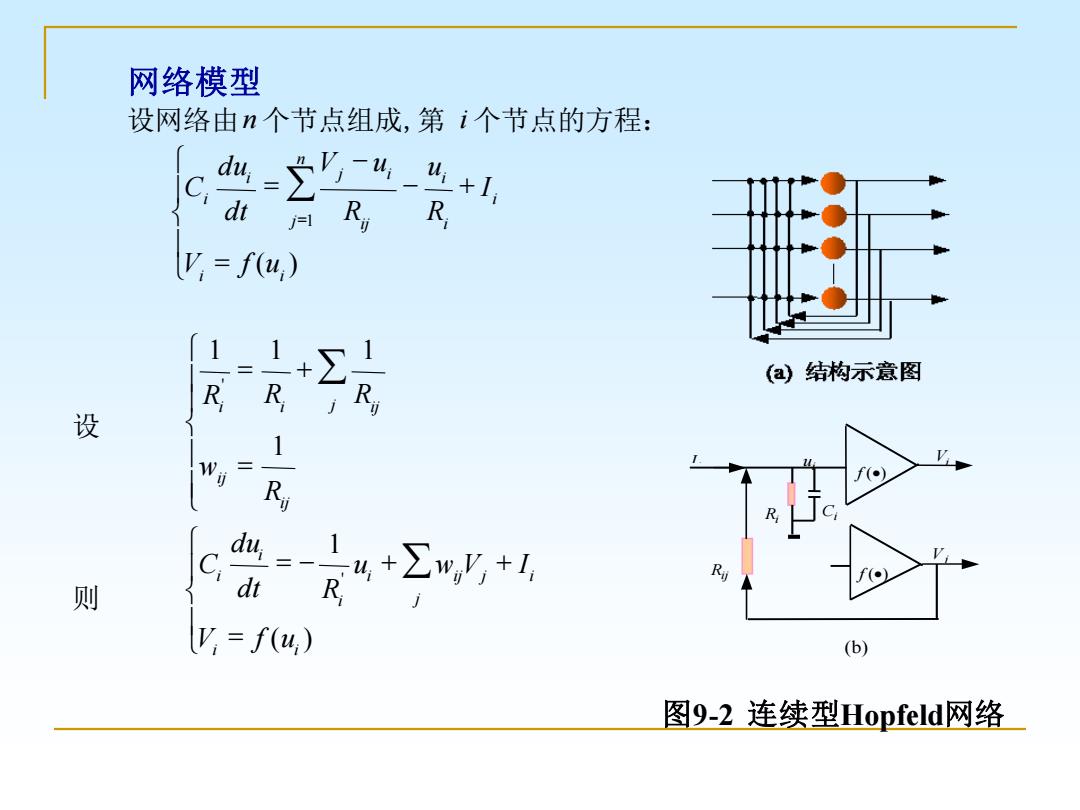
网络模型 设网络由n个节点组成,第i个节点的方程: Ry R j=1 V=f(u,) ()结构示意图 R R R 设 1 R du= 则 C 1 dt 4+∑w,+1 R V,=f(u) (b) 图9-2连续型Hopfeld网络
图9-2 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•) 网络模型 设网络由n 个节点组成,第 i 个节点的方程: = − + − = = ( ) 1 i i n j i i i ij j i i i V f u I R u R V u dt du C 设 1 1 1 1 R R R w R i i j ij ij ij ' = + = 则 C du dt R u w V I V f u i i i i ij j j i i i = − + + = 1 ' ( )
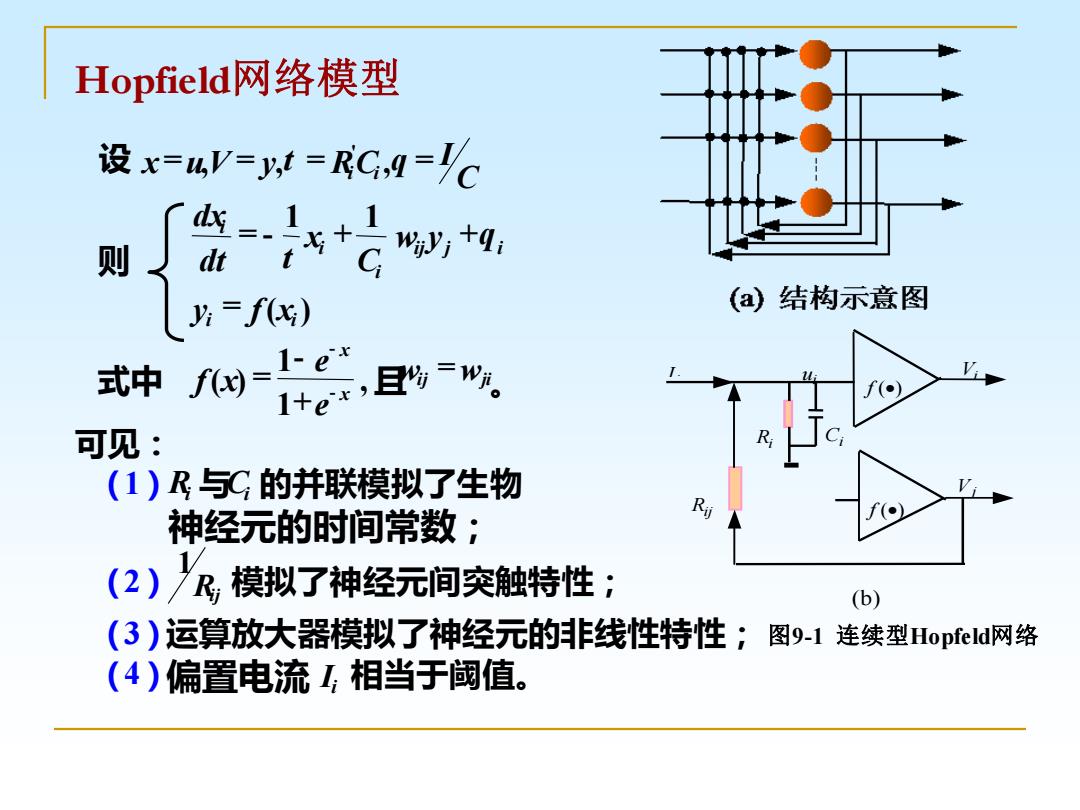
Hopfield网络模型 设x=4V=t=RC,A=C 则 dt 片=fG) (a结构示意图 式中f= 可见: (1)R与C的并联模拟了生物 神经元的时间常数: R (2)£,模拟了神经元间突触特性; (b) (3)运算放大器模拟了神经元的非线性特性;图9-1连续型HopfeldP网络 (4)偏置电流1相当于阈值
Hopfield网络模型 图9-1 连续型Hopfeld网络 (b) Rij Vj Vi Ci Ri i ui I f (•) f (•) 运算放大器模拟了神经元的非线性特性; 设 x uV y RC I i i C = , = , = , = ' t q 则 dx dt x C w y y f x i i i ij j i i i = - + + = 1 1 t q ( ) 式中 f x e e x x ( ) = - + - - 1 1 , 且wij =wji 。 可见: (1)Ri 与Ci 的并联模拟了生物 (2) 1 Rij 模拟了神经元间突触特性; (3) (4)偏置电流 Ii 相当于阈值。 神经元的时间常数;