
大连理工大学博士学位论文 (3)金枪鱼科式:金枪鱼科式作为一种高效的游动方式,适于长时间高速巡游,能 够为人工系统的先进推进器的设计提供一种思路,近来吸引了人们广泛的兴趣。鱼类在 利用金枪鱼模式游动时,主要是由形状为一个锥形水翼,其后掠角大小适中,前缘弯曲, 后缘尖削的刚性月牙形尾鳍的摆动来完成的叫,这类鱼的前半部分身体基本失去柔性, 推进运动产生于尾鳍至尾柄处,其中尾鳍产生了超过90%的推力,像鲨鱼等都采用这种 推进模式游动。 (4)中央鳍/对鳍模式:对于这种MP℉推进方式,推力的产生主要由中央鳍(背鳍、 臀鳍)和对鳍(如胸鳍)等产生,它们由除了尾鳍之外的一些鱼鳍来向前推进),这种 推进模式在低速游动时更具有效率,且鱼主要是用这些鳍的摆动/波动来保持平衡和控制 转向的。 另外,每一种运动模式根据鱼的动作表现的波动频率可以分成波动运动和振动运 动。波动运动是当鱼以波状运动产生推进力时施行的,而当鱼用旋转状的运动来获得自 己的推力时,这种运动该归类到振动运动。这两种运动方式不能明显的区分开来,由于 振动运动是在波动运动时波长很短时的情况。 (a) (b) (c) (④ 图1.2BCF游动模式的分阶段渐变图,(a)鰻鲡模式(b)亚鲹科模式(c)鰺科模式(d金枪鱼科模式1 Fig.1.2 Gradation of BCF swimming movements from(a)anguilliform,through(b)subcarangiform and (c)carangiform to(d)thunniform mode. -3- 万方数据
大连理工大学博士学位论文 (3)金枪鱼科式:金枪鱼科式作为一种高效的游动方式,适于长时间高速巡游,能 够为人工系统的先进推进器的设计提供一种思路,近来吸引了人们广泛的兴趣。鱼类在 利用金枪鱼模式游动时,主要是由形状为一个锥形水翼,其后掠角大小适中,前缘弯曲, 后缘尖削的刚性月牙形尾鳍的摆动来完成的Il¨,这类鱼的前半部分身体基本失去柔性, 推进运动产生于尾鳍至尾柄处,其中尾鳍产生了超过90%的推力,像鲨鱼等都采用这种 推进模式游动。 (4)中央鳍/对鳍模式:对于这种MPF推进方式,推力的产生主要由中央鳍(背鳍、 臀鳍)和对鳍(如胸鳍)等产生,它们由除了尾鳍之外的一些鱼鳍来向前推进【l 21,这种 推进模式在低速游动时更具有效率,且鱼主要是用这些鳍的摆动/波动来保持平衡和控制 转向的。 另外,每一种运动模式根据鱼的动作表现的波动频率可以分成波动运动和振动运 动。波动运动是当鱼以波状运动产生推进力时施行的,而当鱼用旋转状的运动来获得自 己的推力时,这种运动该归类到振动运动。这两种运动方式不能明显的区分开来,由于 振动运动是在波动运动时波长很短时的情况。 ‘,’ 参 (b) \I 、| {t 、3 (c) 、1 II ! (d) 图1.2 BCF游动模式的分阶段渐变图,(a)鳗鲡模式(b)亚鳢科模式(c)鳕科模式(d)金枪鱼科模式【8】 Fig.1.2 Gradation of BCF swimming movements from(a)anguilliform,through(b)subcarangiform and (c)carangiform to(d)thunniform mode. 万方数据
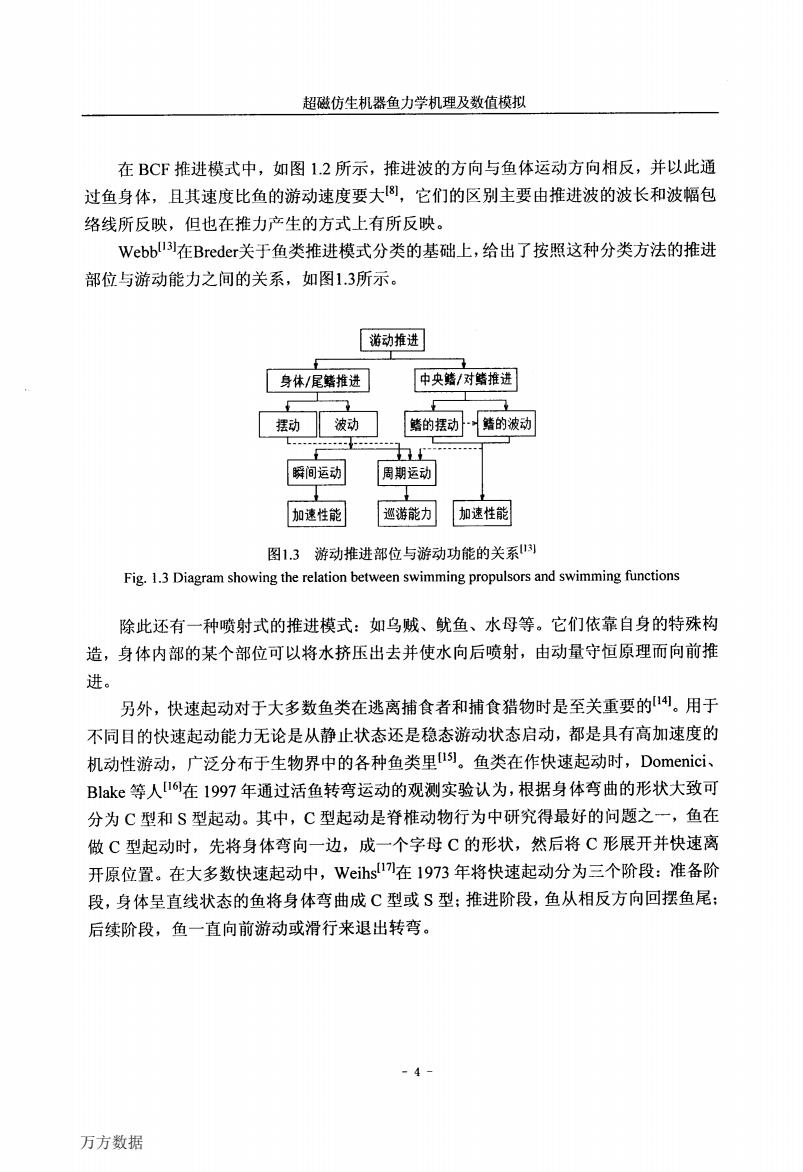
超磁仿生机器鱼力学机理及数值模拟 在BCF推进模式中,如图1.2所示,推进波的方向与鱼体运动方向相反,并以此通 过鱼身体,且其速度比鱼的游动速度要大8,它们的区别主要由推进波的波长和波幅包 络线所反映,但也在推力产生的方式上有所反映。 Webbu在Breder关于鱼类推进模式分类的基础上,给出了按照这种分类方法的推进 部位与游动能力之间的关系,如图1.3所示。 游动推进 身体/尾鳍推进 中央鳍/对鳍推进 摆动 波动 鳍的摆动鳍的波动 瞬间运动 周期运动 加速性能 巡游能力 加速性能 图1.3游动推进部位与游动功能的关系) Fig.1.3 Diagram showing the relation between swimming propulsors and swimming functions 除此还有一种喷射式的推进模式:如乌贼、鱿鱼、水母等。它们依靠自身的特殊构 造,身体内部的某个部位可以将水挤压出去并使水向后喷射,由动量守恒原理而向前推 进。 另外,快速起动对于大多数鱼类在逃离捕食者和捕食猎物时是至关重要的1。用于 不同目的快速起动能力无论是从静止状态还是稳态游动状态启动,都是具有高加速度的 机动性游动,广泛分布于生物界中的各种鱼类里l)。鱼类在作快速起动时,Domenici、 Blake等人16在1997年通过活鱼转弯运动的观测实验认为,根据身体弯曲的形状大致可 分为C型和S型起动。其中,C型起动是脊椎动物行为中研究得最好的问题之一,鱼在 做C型起动时,先将身体弯向一边,成一个字母C的形状,然后将C形展开并快速离 开原位置。在大多数快速起动中,Weihs1在1973年将快速起动分为三个阶段:准备阶 段,身体呈直线状态的鱼将身体弯曲成C型或S型:推进阶段,鱼从相反方向回摆鱼尾: 后续阶段,鱼一直向前游动或滑行来退出转弯。 -4- 万方数据
超磁仿生机器鱼力学机理及数值模拟 在BCF推进模式中,如图1.2所示,推进波的方向与鱼体运动方向相反,并以此通 过鱼身体,且其速度比鱼的游动速度要大‘引,它们的区别主要由推进波的波长和波幅包 络线所反映,但也在推力产生的方式上有所反映。 Webb[131在Breder关于鱼类推进模式分类的基础上,给出了按照这种分类方法的推进 部位与游动能力之间的关系,如图1.3所示。 游动推进 身体/尾鳍推进I I中央鳍/对鳍推进 剿型犁’恒掣 f。;;;1;{f;iii;i:f1—勰’一一一一一一一] 加速性能l l巡游能力I I抽辅MIT龀I北, 图1.3游动推进部位与游动功能的关系I”】 Fig.1.3 Diagram showing the relation between swimming propulsors and swimming functions 除此还有一种喷射式的推进模式:如乌贼、鱿鱼、水母等。它们依靠自身的特殊构 造,身体内部的某个部位可以将水挤压出去并使水向后喷射,由动量守恒原理而向前推 进。 另外,快速起动对于大多数鱼类在逃离捕食者和捕食猎物时是至关重要的【l制。用于 不同目的快速起动能力无论是从静止状态还是稳态游动状态启动,都是具有高加速度的 机动性游动,广泛分布于生物界中的各种鱼类里Il引。鱼类在作快速起动时,Domenici、 Blake等人【161在1997年通过活鱼转弯运动的观测实验认为,根据身体弯曲的形状大致可 分为c型和S型起动。其中,C型起动是脊椎动物行为中研究得最好的问题之一,鱼在 做C型起动时,先将身体弯向一边,成一个字母C的形状,然后将C形展开并快速离 开原位置。在大多数快速起动中,Weihsll。7J在1973年将快速起动分为三个阶段:准备阶 段,身体呈直线状态的鱼将身体弯曲成C型或S型;推进阶段,鱼从相反方向回摆鱼尾; 后续阶段,鱼一直向前游动或滑行来退出转弯。 万方数据

大连理工大学博士学位论文 1.2.2自然界鱼类观察实验 通过对活鱼游动的观察,可以得到鱼类的游动形态,分析鱼类的运动特点,并进行 相应的研究。而高速摄影技术等测试技术的成熟,可以针对极端情况,如捕食和逃逸时 的一些快速起动和快速转弯下的运动学进行观测。中国科技大学的吴燕峰别和敬军9 等分别用该方法定量地研究了斑马鱼为捕食在低速巡游状态下做出S形起动的过程和 鯽鱼在静止状态下的C形起动过程。 然而,对于鱼类游动时鱼身的周围流场,通过肉眼观察或一般的摄影技术就很难发 现其形态。但是,像射线照相技术等测量技术则可以对流场结构做定性分析,而数字粒 子图像测速技术(①PV)可以无需对流场产生干扰,利用对散布在流场中的特殊示踪粒子 通过影像技术进行跟踪,以确定流场中大量空间点上的速度分布。 DPIV技术最先于1995年20应用于水生动物在游动或捕食时所产生的流场测试中。 1997年,Mler2等人通过二维PIV技术定量测量游动胭脂鱼的尾迹,并分析了它的结 构。他们发现,在平稳游动时的鱼身后面的尾迹中,沿着水平中面清楚地显示出反卡门 涡街结构。Lauder和Drucke22在1999年利用多层面的2维DPIV技术测量了稳态游动 的蓝鳃太阳鱼的胸鳍后面的尾迹,揭示出尾迹中的一系列的交错和相互连接的涡环,沿 着这些相互联系的涡环的水平中面,存在推力型尾迹的反卡门涡街。在2000年,他们 又通过慢速和快速游动的鱼的尾迹结构和所产生的力对鱼的游动速度作了水动力学分 析2)。2001年,他们用同样的方法研究了太阳鱼在机动转弯时的尾迹动力学和流体的 作用力2。后来,Ferry-Graham等人2用DPIV技术测量了蓝鳃太阳鱼在捕获食物时的 流场,分析了周围流场的结构。Brenden等人2l利用PIV技术研究了大鲖的机动运动学 和快速C型起动产生的涡尾迹之间的关系,并计算了作用在鱼身上的水动力。Mendelson 等人利用3维合成孔径PIV技术测量了自由游动鱼的尾流,发现在鱼体的尾迹结构中, 显示出有离散的和串联的涡环,以及推力喷流,并计算了尾涡的环量和涡漩脉冲,对尾 流的动力学作了定量分析。Stamhuis等人28利用DPIV技术测量了六种不同雷诺数下, 其相应动物运动产生的流场。Sakakibaral29在2004年利用立体影像PIV技术对活鱼游动 时流场的三个分速度进行了测量,同时利用照相机拍下鱼的影子图像来重建鱼的三维形 状,对所得的鱼尾摆动产生的侧面喷射流和脱落的涡环估算了其脉冲力和时均力。 Flammang等人Bo首次利用散焦DPIV技术测量了水槽中游动的蓝鳃太阳鱼和慈鯛的尾 鳍在游动时脱落的三维涡环,并使其呈现出了完整的可视化,且测量结果还显示出了一 些由背鳍和殿鳍产生的小一些的涡。 -5… 万方数据
大连理工大学博士学位论文 1.2.2自然界鱼类观察实验 通过对活鱼游动的观察,可以得到鱼类的游动形态,分析鱼类的运动特点,并进行 相应的研究。而高速摄影技术等测试技术的成熟,可以针对极端情况,如捕食和逃逸时 的一些快速起动和快速转弯下的运动学进行观测。中国科技大学的吴燕峰【l引和敬军【l刈 等分别用该方法定量地研究了斑马鱼为捕食在低速巡游状态下做出S形起动的过程和 鲫鱼在静止状态下的C形起动过程。 然而,对于鱼类游动时鱼身的周围流场,通过肉眼观察或~般的摄影技术就很难发 现其形态。但是,像射线照相技术等测量技术则可以对流场结构做定性分析,而数字粒 子图像测速技术(DPIV)可以无需对流场产生干扰,利用对散布在流场中的特殊示踪粒子 通过影像技术进行跟踪,以确定流场中大量空间点上的速度分布。 DPIV技术最先于1995年【20J应用于水生动物在游动或捕食时所产生的流场测试中。 1997年,Miiller[211等人通过二维PIV技术定量测量游动胭脂鱼的尾迹,并分析了它的结 构。他们发现,在平稳游动时的鱼身后面的尾迹中,沿着水平中面清楚地显示出反卡门 涡街结构。Lauder和Drucke[22】在1 999年利用多层面的2维DPIV技术测量了稳态游动 的蓝鳃太阳鱼的胸鳍后面的尾迹,揭示出尾迹中的一系列的交错和相互连接的涡环,沿 着这些相互联系的涡环的水平中面,存在推力型尾迹的反卡门涡街。在2000年,他们 又通过慢速和快速游动的鱼的尾迹结构和所产生的力对鱼的游动速度作了水动力学分 析【231。2001年,他们用同样的方法研究了太阳鱼在机动转弯时的尾迹动力学和流体的 作用力【241。后来,Ferry.Graham等人【251用DPIV技术测量了蓝鳃太阳鱼在捕获食物时的 流场,分析了周围流场的结构。Brenden等人【26J利用PIV技术研究了大鲴的机动运动学 和快速C型起动产生的涡尾迹之间的关系,并计算了作用在鱼身上的水动力。Mendelson 等人【27】利用3维合成孔径PIV技术测量了自由游动鱼的尾流,发现在鱼体的尾迹结构中, 显示出有离散的和串联的涡环,以及推力喷流,并计算了尾涡的环量和涡漩脉冲,对尾 流的动力学作了定量分析。Stamhuis等人12叫利用DPIV技术测量了六种不同雷诺数下, 其相应动物运动产生的流场。Sakal【ibara【29J在2004年利用立体影像P1V技术对活鱼游动 时流场的三个分速度进行了测量,同时利用照相机拍下鱼的影子图像来重建鱼的三维形 状,对所得的鱼尾摆动产生的侧面喷射流和脱落的涡环估算了其脉冲力和时均力。 Flammang等人【30J首次利用散焦DPIV技术测量了水槽中游动的蓝鳃太阳鱼和慈鲷的尾 鳍在游动时脱落的三维涡环,并使其呈现出了完整的可视化,且测量结果还显示出了一 些由背鳍和殿鳍产生的小一些的涡。 万方数据

超磁仿生机器鱼力学机理及数值模拟 人们通过分析游动鱼周围的流场结构以及鱼游动时的一些动作所留下的尾迹结构, 以及对作用在鱼身上的流体的力、力矩,以及鱼游动过程中的能量分布等做定量计算, 从而找到鱼类高效游动的原因。 1.2.3鱼类推进机理的研究 作用在游动鱼身上的力在竖直方向有重力、浮力和水动升力,在水平方向有推力和 阻力。水的密度是非常接近海洋动物身体密度的,从而基本能够承受鱼身的自身重力。 对于浮力为负的鱼,必须产生水动升力来提供浮力和平衡竖直方向的力,以确保它们不 沉下去,很多鱼是通过在持续游动时展开它们的胸鳍来达到此目的的。但是,这样会使 其游动的时候产生阻力,从而将打破水平方向的力的平衡。 当鱼以恒定的速度推进自己前进时,由动量守恒定律要求作用在鱼身上的力和弯矩是 平衡的。因此,鱼利用水的作用产生的总的推力必需等于它向前游动时遇到的总的阻力。 作用在鱼身上的压差阻力、升力和加速反力都能作为推力和阻力。但是,由于升力的产 生跟鱼的推进部位的自主运动是相关的,它在鱼突然停止时,仅仅能充当阻力。另外, 粘滞力总是充当阻力的作用。而对于身体的惯性虽然不参与动量传递,它充当了水的阻 力,因为它阻碍加速而保持运动状态。总之,决定这些力对推进力和阻力的动量传递机 制的贡献率的主要因素是:雷诺数、斯德鲁哈尔数和鱼的形状。 为了探究鱼类的游动模式的机理,国内外科研人员建立了一系列的鱼类推进机理的 理论模型。来自不同背景的科学家试图用数学模型来描述观察到的鱼的运动学问题。由 于生物运动过程中固有的可变性和复杂性,相比于其他工程领域其精确性和重复性的实 验和测量会受到限制。早期,Taylor32(1952)为分析、计算微小水生动物运动的流体 力,建立了一种抗力水动力模型,他是利用静态流体理论基于准静态逼近的方法来建立 抗力理论,这对小雷诺数时的运动规律能够很好的解释。对于一般的水生动物,其在水 中的运动通常表现为由高柔韧性的升力面作大幅度的拍动,这时,对于身体大于几毫米、 游动速度为每秒几倍体长时,则为大雷诺数范围。对它们的推进部位,根据升力面的高 宽比有两种情况,小的展弦比和大展弦比。对这两种情况,在传统的势流理论中,可以 采用不同的理论进行分析。 对小的展弦比(细长的动物,像鳗鱼),可用细长体理论进行分析。源于空气动力 学的细长体理论,形成Lighthill在1960年提出的细长体理论[的基础,这适合于分析 鱼类的亚鲹科和鲹科游动模式。对于大的展弦比(像月牙型尾鳍,如金枪鱼),可用二 维波动板理论或升力面理论进行分析。Lighthil训是第一个应用简单的二维线性机翼理论 于新月形尾鳍推进模型中的3,他在1970年假设流体为非粘性的和无旋的,并用势流 -6 万方数据
超磁仿生机器鱼力学机理及数值模拟 人们通过分析游动鱼周围的流场结构以及鱼游动时的一些动作所留下的尾迹结构, 以及对作用在鱼身上的流体的力、力矩,以及鱼游动过程中的能量分布等做定量计算, 从而找到鱼类高效游动的原斟31J。 1.2.3鱼类推进机理的研究 作用在游动鱼身上的力在竖直方向有重力、浮力和水动升力,在水平方向有推力和 阻力。水的密度是非常接近海洋动物身体密度的,从而基本能够承受鱼身的自身重力。 对于浮力为负的鱼,必须产生水动升力来提供浮力和平衡竖直方向的力,以确保它们不 沉下去,很多鱼是通过在持续游动时展开它们的胸鳍来达到此目的的。但是,这样会使 其游动的时候产生阻力,从而将打破水平方向的力的平衡。 当鱼以恒定的速度推进自己前进时,由动量守恒定律要求作用在鱼身上的力和弯矩是 平衡的。因此,鱼利用水的作用产生的总的推力必需等于它向前游动时遇到的总的阻力。 作用在鱼身上的压差阻力、升力和加速反力都能作为推力和阻力。但是,由于升力的产 生跟鱼的推进部位的自主运动是相关的,它在鱼突然停止时,仅仅能充当阻力。另外, 粘滞力总是充当阻力的作用。而对于身体的惯性虽然不参与动量传递,它充当了水的阻 力,因为它阻碍加速而保持运动状态。总之,决定这些力对推进力和阻力的动量传递机 制的贡献率的主要因素是:雷诺数、斯德鲁哈尔数和鱼的形状。 为了探究鱼类的游动模式的机理,国内外科研人员建立了一系列的鱼类推进机理的 理论模型。来自不同背景的科学家试图用数学模型来描述观察到的鱼的运动学问题。由 于生物运动过程中固有的可变性和复杂性,相比于其他工程领域其精确性和重复性的实 验和测量会受到限制。早期,Taylor[32】(1952)为分析、计算微小水生动物运动的流体 力,建立了一种抗力水动力模型,他是利用静态流体理论基于准静态逼近的方法来建立 抗力理论,这对小雷诺数时的运动规律能够很好的解释。对于一般的水生动物,其在水 中的运动通常表现为由高柔韧性的升力面作大幅度的拍动,这时,对于身体大于几毫米、 游动速度为每秒几倍体长时,则为大雷诺数范围。对它们的推进部位,根据升力面的高 宽比有两种情况,小的展弦比和大展弦比。对这两种情况,在传统的势流理论中,可以 采用不同的理论进行分析。 对小的展弦比(细长的动物,像鳗鱼),可用细长体理论进行分析。源于空气动力 学的细长体理论,形成Lighthill在1960年提出的细长体理论【33J的基础,这适合于分析 鱼类的亚鳢科和鲶科游动模式。对于大的展弦比(像月牙型尾鳍,如金枪鱼),可用二 维波动板理论或升力面理论进行分析。Lighthill是第一个应用简单的二维线性机翼理论 于新月形尾鳍推进模型中的【34】,他在1970年假设流体为非粘性的和无旋的,并用势流 万方数据

大连理工大学博士学位论文 理论来计算了小振幅振荡时新月形尾鳍的推力。WuB在1971年用这样的二维模型来计 算推进效率,可以实现接近于100%。Chopral36在1976年建立了一个基于脉冲方法的大 幅度二维理论。然后,Chopra通过扩展到三维空间,在限于矩形翼型和小振幅摆动的情 况下,建立了一个基于涡分布的模型B)。Chopra和Kambel381在1977年利用一种三维非 定常的升力面理论研究了不同形状的翼形的推力的产生。LanB在1979年使用非稳态准 涡格方法,也计算了一个三维模型的问题。由于在以上所有的这些理论模型中,都假设 鱼尾是刚性的,Katz和Weihs40]在1978年研究了在二维情况下进行大幅度运动的鱼尾 的弦向柔韧性的影响。Ahamadi和Widnall!在l986年建立了一个线性化的低频率非定 常升力线理论。Bose和Lien42在1989年建立了一个考虑小幅度俯仰运动的薄片理论, 用来计算以类似原理工作的鲸鱼鳍的水动力性能。Cheng和Murillo1在1984年考虑月 牙形尾鳍的弯曲中心线,建立了一个三维理论模型,并随后用以确定后掠角和中心线曲 率的影响。随后,Cheng等人在I991年又采用非定常涡环法分析了三维的三角形的 水翼。Liu和Bose1在1997年用时域面板法研究了关于具有弦向柔韧性的三维薄板的 推进效率。以上的理论的大多数都假设了尾迹后面的平面涡流,而没有考虑发展起来的 旋转漩涡模式。 对于尾迹涡效应所产生的推进机理,Lighthil和Videler2l认为反卡门涡街仅只是 鱼尾鳍运动的结果。Rosn等人4进行的鲹科游动模式的鱼的流动实验显示,附着的漩 涡是由鱼的前半部分身体所产生,于是他提出了一个“涡桩”(Vortex Peg)原理,即鱼身 穿过这些漩涡,并通过吸收漩涡的旋转能量而向前运动。Muller等人2建立了一个“波 动泵”(Undulating Pump)的原理,即在鱼周围流场的压力和吸力区域生成一个环流并围 绕在身体的拐点周围,这个环流沿着身体向后传播,当到达鱼的尾鳍时,与鱼尾产生的 附着漩涡相互作用,形成离散的漩涡脱落在尾迹中。Triantafyllou481提出了一个类似的 原理,认为鱼可以对能量进行回收以及减小体表阻力。这些原理可能会为长久以来困扰 科学家的“Gry悖论”提供一个解释。由鯖科鱼中经常观察到鱼的集群行为,鱼群会对 涡量进行控制,这种集群行为会产生一种槽道效应9,即让鱼群保持紧密游动时,可以 使涡街两边的流动得到充分利用。当在同一列的鱼与相邻的鱼以相反的相位游动时这个 优势会更大,由此提出一个细长菱形图案作为鱼群的最佳基本结构S0 另外,以上这些理论都是先通过假定的鱼体干曲线进行水动力学分析的,而不是鱼类 自主游动时的真实身体波动曲线。 7- 万方数据
大连理工大学博士学位论文 理沦来计算了小振幅振荡时新月形尾鳍的推力。Wu[35J在1971年用这样的二维模型来计 算推进效率,可以实现接近于100%。Chopra[36J在1976年建立了一个基于脉冲方法的大 幅度二维理论。然后,Chopra通过扩展到三维空间,在限于矩形翼型和小振幅摆动的情 况下,建立了一个基于涡分布的模型13列。Chopra和Kambe[38】在1977年利用一种三维非 定常的升力面理论研究了不同形状的翼形的推力的产生。Lan[39J在1979年使用非稳态准 涡格方法,也计算了一个三维模型的问题。由于在以上所有的这些理论模型中,都假设 鱼尾是刚性的,Katz和Weihs[40J在1978年研究了在二维情况下进行大幅度运动的鱼尾 的弦向柔韧性的影响。Ahamadi和Widnall[4lJ在1986年建立了一个线性化的低频率非定 常升力线理论。Bose和Lienl42J在1989年建立了一个考虑小幅度俯仰运动的薄片理论, 用来计算以类似原理工作的鲸鱼鳍的水动力性能。Cheng和Murillol43J在1984年考虑月 牙形尾鳍的弯曲中心线,建立了一个三维理论模型,并随后用以确定后掠角和中心线曲 率的影响。随后,Cheng等人【44J在1991年又采用非定常涡环法分析了三维的三角形的 水翼。Liu和Bose[45]在1997年用时域面板法研究了关于具有弦向柔韧性的三维薄板的 推进效率。以上的理论的大多数都假设了尾迹后面的平面涡流,而没有考虑发展起来的 旋转漩涡模式。 对于尾迹涡效应所产生的推进机理,Lighthill[46J和Videler[12】认为反卡门涡街仅只是 鱼尾鳍运动的结果。Rosen等人【4 7J进行的鲮科游动模式的鱼的流动实验显示,附着的漩 涡是由鱼的前半部分身体所产生,于是他提出了一个“涡桩”(Vortex Peg)原理,即鱼身 穿过这些漩涡,并通过吸收漩涡的旋转能量而向前运动。Mfiller等人【21】建立了一个“波 动泵”(Undulming Pump)的原理,即在鱼周围流场的压力和吸力区域生成一个环流并围 绕在身体的拐点周围,这个环流沿着身体向后传播,当到达鱼的尾鳍时,与鱼尾产生的 附着漩涡相互作用,形成离散的漩涡脱落在尾迹中。Triantafyllout48】提出了一个类似的 原理,认为鱼可以对能量进行回收以及减小体表阻力。这些原理可能会为长久以来困扰 科学家的“Gray悖论”提供一个解释。由鲭科鱼中经常观察到鱼的集群行为,鱼群会对 涡量进行控制,这种集群行为会产生一种槽道效应【491,即让鱼群保持紧密游动时,可以 使涡街两边的流动得到充分利用。当在同-YU的鱼与相邻的鱼以相反的相位游动时这个 优势会更大,由此提出一个细长菱形图案作为鱼群的最佳基本结构【50】。 另外,以上这些理论都是先通过假定的鱼体干曲线进行水动力学分析的,而不是鱼类 自主游动时的真实身体波动曲线。 万方数据