
判断题 1凡是运动的质点都有惯性力 2惯性力是作用在质点上的 3质点在空中运动,只受到重力作用, 当质点作自由落体运动,质点被上抛,质点被平抛时, 质点的惯性力是不相同 质点的惯性力只与那两个必要条件有关 6
6 判断题 1 凡是运动的质点都有惯性力 2 惯性力是作用在质点上的 3 质点在空中运动,只受到重力作用, 质点的惯性力只与那两个必要条件有关 当质点作自由落体运动,质点被上抛,质点被平抛时, 质点的惯性力是不相同
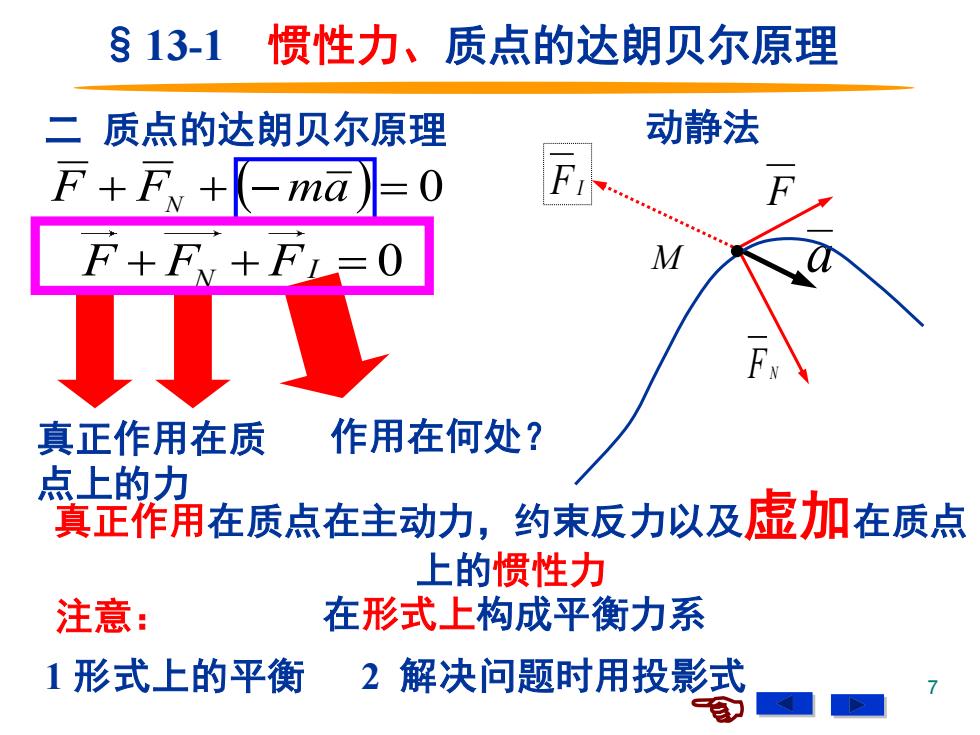
§13-1 惯性力、质点的达朗贝尔原理 二 质点的达朗贝尔原理 动静法 F+F+-mā=0 F+E+FL=0 M 真正作用在质 作用在何处? 点上的力 真正作用在质点在主动力,约束反力以及虚加在质点 上的惯性力 注意: 在形式上构成平衡力系 1形式上的平衡衡 2解决问题时用投影式
7 真正作用在质点在主动力,约束反力以及虚加在质点 上的惯性力 二 质点的达朗贝尔原理 F F N a FI I 0 M F F F + + = N 真正作用在质 点上的力 作用在何处? §13-1 惯性力、质点的达朗贝尔原理 F + FN + (− ma ) = 0 注意: 在形式上构成平衡力系 1 形式上的平衡 2 解决问题时用投影式 动静法

§13-1 惯性力、质点的达朗贝尔原理 三思考题 F+F+F1=0 1应用动静法时,对静止的质点是否需要加惯性力? 2对运动的质点是否都要加惯性力? 3应用动静法可以解决什么样的问题? 8
8 三 思考题 1 应用动静法时 ,对静止的质点是否需要加惯性力? 2 对运动的质点是否都要加惯性力? 3 应用动静法可以解决什么样的问题? F F F + + = N I 0 §13-1 惯性力、质点的达朗贝尔原理

例1圆盘可绕轴0转动,质量不计。其上缠有一质量不 计的绳,绳不可伸长,绳下端分别吊重物AB。 若圆盘半径为Rr,重物AB的质量MA大于MB 并设绳与圆盘间无相对滑动。偌盘的角加速度为已知 要求:1计算A、B惯性力的大小 2标上惯性力的方向 08 注意:虚加的位置 实线??虚线
9 B A O 例1 圆盘可绕轴O转动,质量不计。其上缠有一质量不 计的绳,绳不可伸长,绳下端分别吊重物A B 。 若圆盘半径为 R r,重物A B 的质量MA大于MB 并设绳与圆盘间无相对滑动。若盘的角加速度为已知 要求: 1 计算A 、B惯性力的大小 2 标上惯性力的方向 注意:虚加的位置 实线 ??虚线

§13-2 质点系的达朗贝尔原理 质点系的的达朗贝尔原理 F+F+F=0 F+F F=0 对于质点系中的质点,所受主动力、约束力实际上就 是外力、内力 厅+FF=( (i=l-n) =∑0∑网+∑万.=0 M,=Σa匠)Ha,Σa,)=0 ΣF0=0,ΣM(E=0, 10
10 §13-2 质点系的达朗贝尔原理 一、质点系的的达朗贝尔原理 Fi + FNi + FIi = 0 ( ) ( ) + + I i = 0 i i e Fi F F ( ) ( ) ' = + + Ii = 0 i i e FR Fi F F (i=1-n) 对于质点系中的质点,所受主动力、约束力实际上就 是外力、内力 ( ) ( ) ( ) = + ( )+ o ( Ii)= 0 i o i e Mo Mo Fi M F M F ( ) ( ) = 0, ( )= 0, i o i i Fi M F (i=1-n) F F F + + = N I 0