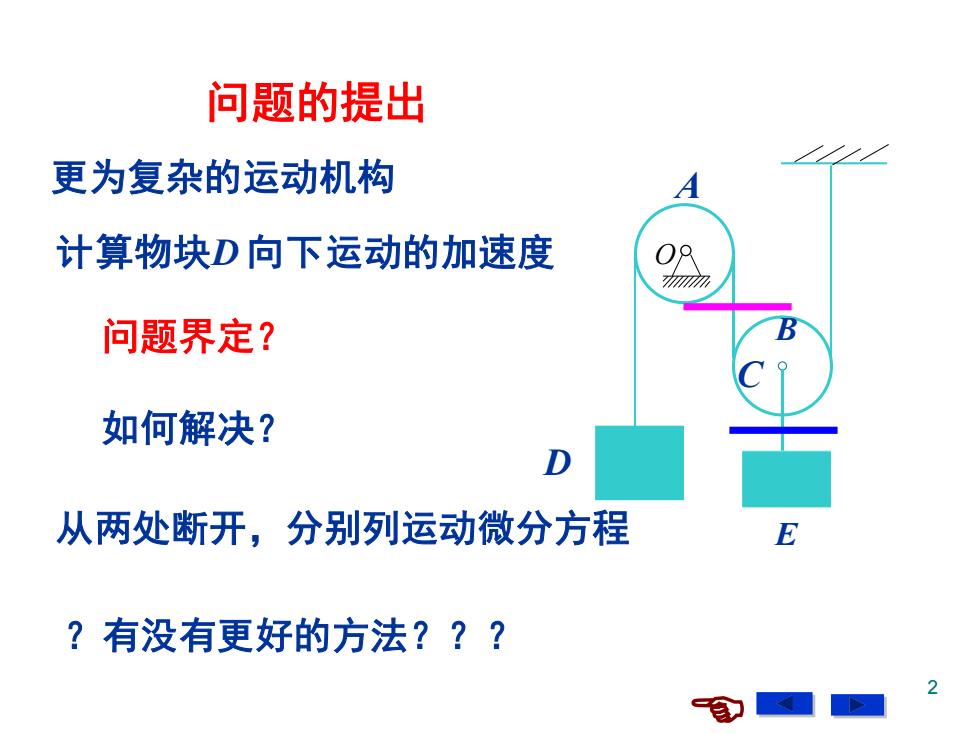
问题的提出 更为复杂的运动机构 计算物块D向下运动的加速度 OR m加 问题界定? 如何解决? D 从两处断开,分别列运动微分方程 ?有没有更好的方法???
2 O D C A B E 问题的提出 更为复杂的运动机构 计算物块D 向下运动的加速度 如何解决? 从两处断开,分别列运动微分方程 ?有没有更好的方法??? 问题界定?

第十二章 动能定理 3
3 第十二章 动 能 定 理

本章教学目标 ★★★1会计算力的功、会计算动能 ”★★★2牢记动能定理,并会应用 ★★★★3牢记动力学普遍定理、并会综合应用
4 本章教学目标 ❖ ★★★ 2 牢记动能定理,并会应用 ★ ★ ★ 1 会计算力的功 、会计算动能 ★★★★ 3 牢记动力学普遍定理、并会综合应用

本次课的内容 1力的功(总结+答疑) 2动能 3动能定理 本次课的教学目标 1 会计算动能、会计算力的功(作业1+报告) 2牢记动能定理的内容、特点,并会应用( 作业2) 本次课的难点 1选定理 2选定理 3选定理 5
5 本次课的内容 2 动能 本次课的教学目标 本次课的难点 3 动能定理 2 牢记动能定理的内容、特点,并会应用 (作业2) 1 会计算动能、会计算力的功(作业1+报告) 1 力的功(总结+答疑) 1 选定理 2 选定理 3 选定理

§12一1力的功 1力的功是代数量 恩格斯说功是从量的方面看的 2变力功的计算 δW适动形式的变化 变力功的计算一元功表达式 (1)自然表达式 oW !!适用于轨迹已知的情况下!! (2)矢量表达式(注意定义) 受力物体上的作用点的微小位移 (3)直角坐标表达式
6 2 变力功的计算 (1)自然表达式 F ds = M M ds F = F ds cos (+) §12-1 力的功 W 1力的功是代数量 恩格斯说功是从量的方面看的 运动形式的变化 W !!适用于轨迹已知的情况下!! 变力功的计算—元功表达式 (2)矢量表达式(注意定义) (3)直角坐标表达式 受力物体上的作用点的微小位移