
Analyzing the running time BOUNDEDSEARCHTREE(G,k)is a recursive program. Each time it decreases k by one and branches to two BOUNDEDSEARCHTREE(-k-1). Thus the number of total running step is roughly 21G
Analyzing the running time I BoundedSearchTree(G, k) is a recursive program. I Each time it decreases k by one and branches to two BoundedSearchTree(−, k − 1). I Thus the number of total running step is roughly 2 k · |G|

The comparison Algorithm running time n=10andk=6 BRUTEFORCE nkfr 10000000 BOUNDEDSEARCHTREE 2-n 640 As we have assumed k is a constant,BoUNDEDSEARCHTREE is a linear time algorithm
The comparison Algorithm running time n = 10 and k = 6 BruteForce n k+1 10000000 BoundedSearchTree 2 k · n 640 As we have assumed k is a constant, BoundedSearchTree is a linear time algorithm

Another more sophisticated linear time algorithm Let G be a graph and k E N. (i)In linear time,we can compute a graph G'and k'sk such that G has a vertex cover of size at most k G'has a vertex cover of size at most k'. Moreover the number of vertices in G'is at most k2+k. (ii)We use BRUTEFORCE on (G',k'). Step(i)is known as Buss'kernelization
Another more sophisticated linear time algorithm Let G be a graph and k ∈ N. (i) In linear time, we can compute a graph G0 and k 0 6 k such that G has a vertex cover of size at most k ⇐⇒ G 0 has a vertex cover of size at most k 0 . Moreover the number of vertices in G0 is at most k 2 + k. (ii) We use BruteForce on (G0 , k 0 ). Step (i) is known as Buss’ kernelization
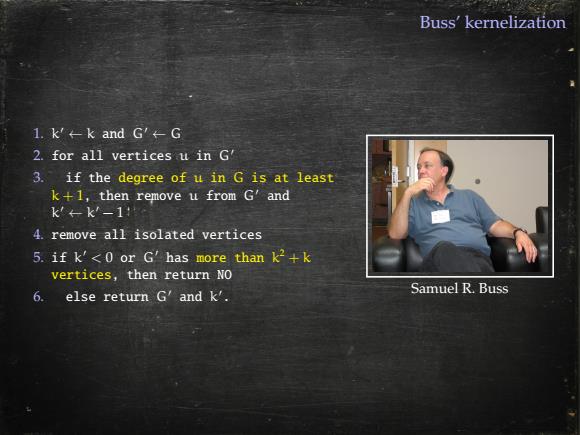
Buss'kernelization 1.k'-k and G'←G 2.for all vertices u in G' 3.if the degree of u in G is at least k+1,then remove u from G'and k-k-1 4.remove all isolated vertices 5.if k'<0 or G'has more than k2+k vertices,then return NO 6.else return G'and k'. Samuel R.Buss
Buss’ kernelization 1. k 0 ← k and G0 ← G 2. for all vertices u in G0 3. if the degree of u in G is at least k + 1, then remove u from G0 and k 0 ← k 0 − 1 4. remove all isolated vertices 5. if k 0 < 0 or G0 has more than k 2 + k vertices, then return NO 6. else return G0 and k 0. Samuel R. Buss

Recall Let G be a graph and k∈N (i)In linear time,we can compute a graph G'and k's k such that G has a vertex cover of size at most k ←→G'has a vertex cover of size at most k'. Moreover the number of vertices in G'is at most k2+k. (ii)We use BRUTEFORCE on (G',k'). This leads to an algorithm of running time 2k2+k.n with the constant worse than the bounded search tree
Recall Let G be a graph and k ∈ N. (i) In linear time, we can compute a graph G0 and k 0 6 k such that G has a vertex cover of size at most k ⇐⇒ G 0 has a vertex cover of size at most k 0 . Moreover the number of vertices in G0 is at most k 2 + k. (ii) We use BruteForce on (G0 , k 0 ). This leads to an algorithm of running time 2 k 2+k · n with the constant worse than the bounded search tree