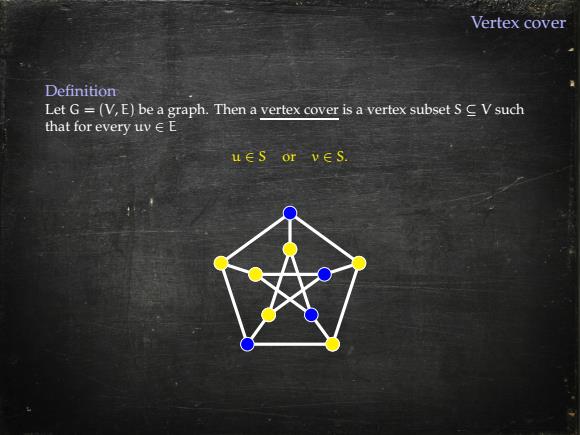
Vertex cover Definition Let G=(V,E)be a graph.Then a vertex cover is a vertex subset S C V such that for every uv∈E ues or ves
Vertex cover Definition Let G = (V, E) be a graph. Then a vertex cover is a vertex subset S ⊆ V such that for every uv ∈ E u ∈ S or v ∈ S

The main question of this talk FOR EACH FIXED K,WHAT IS THE BEST ALGORITHM TO FIND A VERTEX COVER OF SIZE AT MOST K OR REPORT THERE IS NONE?
The main question of this talk For each fixed k, what is the best algorithm to find a vertex cover of size at most k or report there is none?

The most naive algorithm BRUTEFoRCE(G,k) 1.For each subset ScV with ISlsk 2.if s is a vertex cover of G,then output S and return 3.output NO. The number of its running steps is roughly IG+1
The most naive algorithm BruteForce(G, k) 1. For each subset S ⊆ V with |S| 6 k 2. if S is a vertex cover of G, then output S and return 3. output NO. The number of its running steps is roughly |G| k+1

Another naive algorithm BouNDEDSEARCHTREE(G,k) Rodney G.Downey Michael R.Fellows
Another naive algorithm BoundedSearchTree(G, k) Rodney G. Downey Michael R. Fellows

Another naive algorithm BouNDEDSEARCHTREE(G,k) 1.If k<0 then return NO 2.If G has no edge then return S=0 3.else 4. choose an arbitrary edge uv in G 5 remove,u from G and let Gu be the resulting graph 6. call BOUNDEDSEARCHTREE(Gu,k-1) 7 if it returns a vertex cover Su then return SUfu) 8. remove v from G and let G.be the resulting graph 9 call BOUNDEDSEARCHTREE(Gy,k-1) 10. if it returns a vertex cover S then return SU(v) 11. return NO
Another naive algorithm BoundedSearchTree(G, k) 1. If k < 0 then return NO 2. If G has no edge then return S = ∅ 3. else 4. choose an arbitrary edge uv in G 5. remove u from G and let Gu be the resulting graph 6. call BoundedSearchTree(Gu, k − 1) 7. if it returns a vertex cover Su then return Su ∪ {u} 8. remove v from G and let Gv be the resulting graph 9. call BoundedSearchTree(Gv, k − 1) 10. if it returns a vertex cover Sv then return Sv ∪ {v} 11. return NO