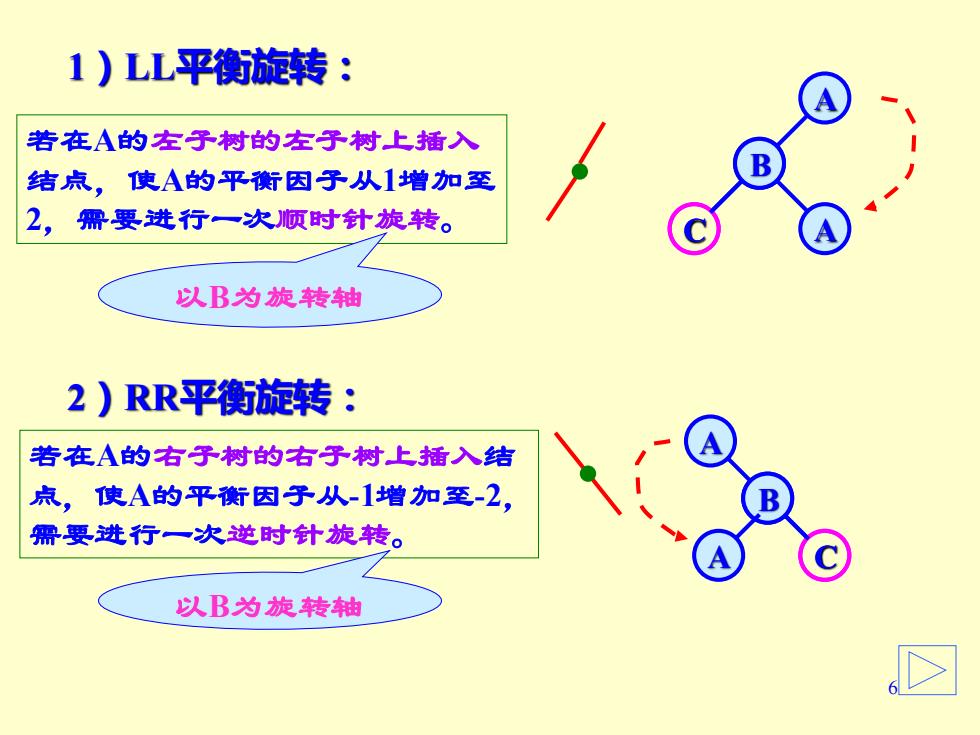
1)LL平衡旋转: 若在A的左子树的左子树上插入 结点,使A的平衡因子从1增加至 2,需要进行一次顺时针旋转。 以B为旋转轴 2)RR平衡旋转: 若在A的右子树的右子树上插入结 点,使A的平衡因子从-1增加至-2, B 需要进行一次逆时针旋转。 以B为旋转轴
6 若在A的左子树的左子树上插入 结点,使A的平衡因子从1增加至 2,需要进行一次顺时针旋转。 A B C A 若在A的右子树的右子树上插入结 点,使A的平衡因子从-1增加至-2, 需要进行一次逆时针旋转。 2)RR平衡旋转: A B A C 1)LL平衡旋转: 以B为旋转轴 以B为旋转轴
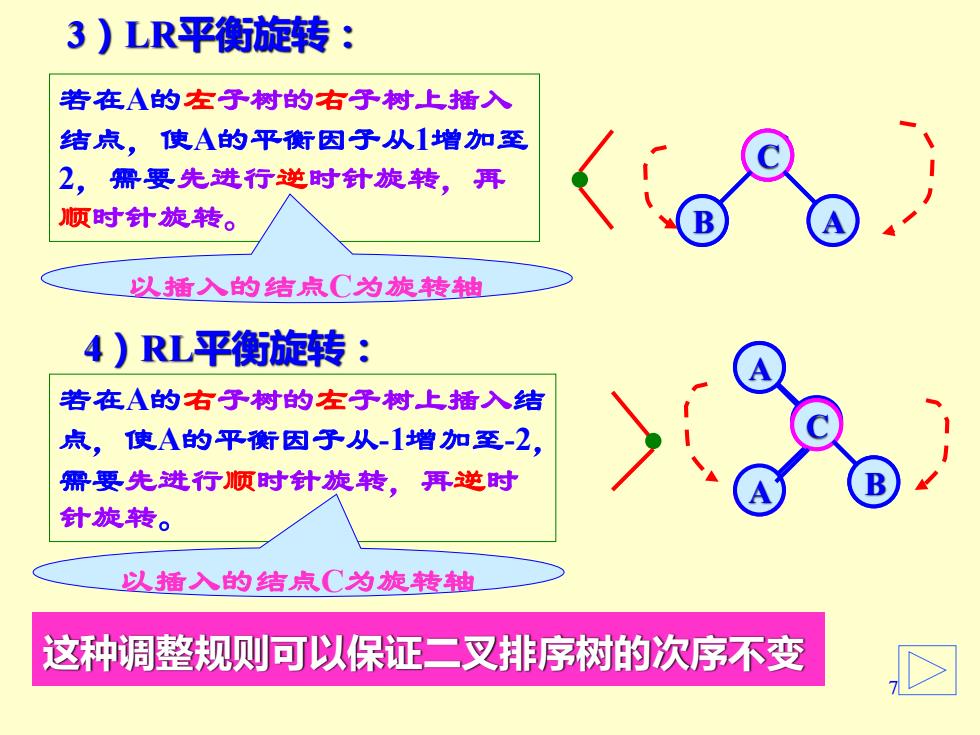
3)LR平衡旋转: 若在A的左子树的右子树上插入 结点,使A的平衡因子从1增加至 2,需要先进行逆时针旋转,再 顺时针旋转。 以插入的结点C为旋转轴 4)RL平衡旋转: 若在A的右子树的左子树上插入结 点,使A的平衡因子从-1增加至-2, 需要先进行顺时针旋转,再逆时 针旋转。 以插入的结点C为旋转轴 这种调整规则可以保证二叉排序树的次序不变
7 A B C 若在A的右子树的左子树上插入结 点,使A的平衡因子从-1增加至-2, 需要先进行顺时针旋转,再逆时 针旋转。 4)RL平衡旋转: A B C A B C A 若在A的左子树的右子树上插入 结点,使A的平衡因子从1增加至 2,需要先进行逆时针旋转,再 顺时针旋转。 3)LR平衡旋转: A B C 这种调整规则可以保证二叉排序树的次序不变 以插入的结点C为旋转轴 以插入的结点C为旋转轴 B A C
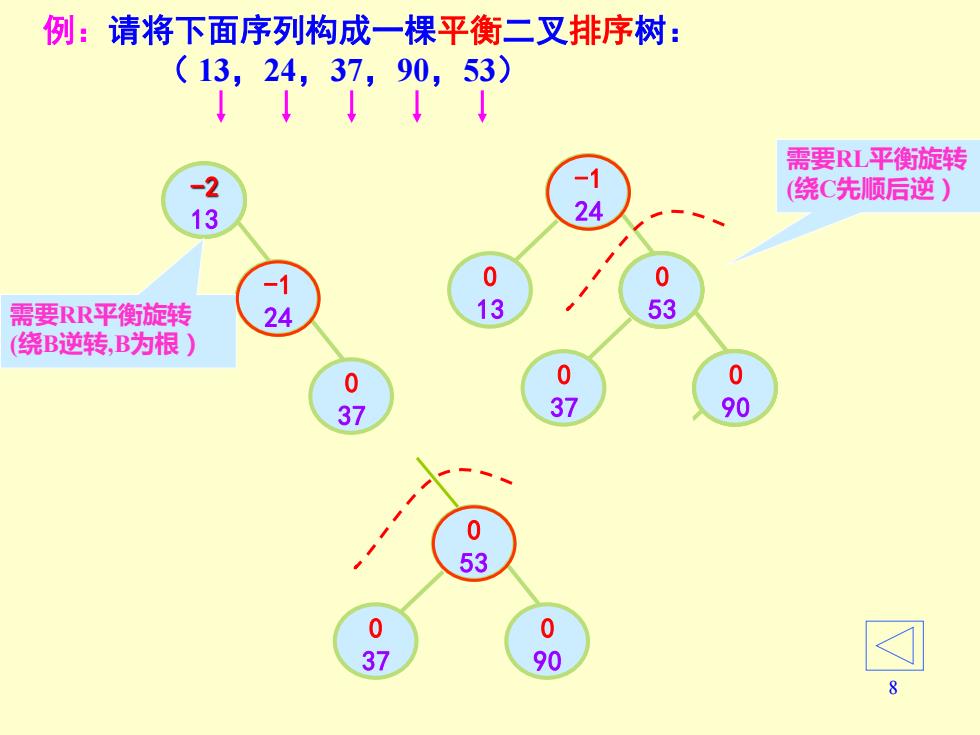
例:请将下面序列构成一棵平衡二叉排序树: (13,24,37,90,53) ↓↓↓↓°↓ 需要RL平衡旋转 2 (绕C先顺后逆) 13 24 1 0 0 需要RR平衡旋转 24 13 53 绕B逆转,B为根) 0 0 0 37 37 90 0 53 0 0 37 90
8 0 13 0 37 0 24 例:请将下面序列构成一棵平衡二叉排序树: ( 13,24,37,90,53) 0 13 0 37 -1 0 24 -1 -2 13 需要RR平衡旋转 (绕B逆转,B为根) 0 90 -1 24 -1 37 0 53 1 90 -2 37 需要RL平衡旋转 (绕C先顺后逆) 0 37 0 90 0 53 0 37 0 90 0 53

9.4哈希查找表 一、哈希表的概念 二、哈希函数的构造方法 三、冲突处理方法 四、哈希表的查找及分析 D
9 9.4 哈希查找表 一、哈希表的概念 二、哈希函数的构造方法 三、冲突处理方法 四、哈希表的查找及分析

一、哈希表的概念 哈希表:即散列存储结构。 散列法存储的基本思想:建立关键码字与其存储位置的对应 关系,或者说,由关键码的值决定数据的存储地址。 优点:查找速度极快(O(1)),查找效率与元素个数n无关! 例1:若将学生信息按如下方式存入计算机,如: 将2001011810201的所有信息存入V[01]单元: 将2001011810202的所有信息存入V[02]单元; 将2001011810231的所有信息存入V[31]单元。 欲查找学号为2001011810216的信息,便可直接访问V[16]」
10 一、哈希表的概念 哈希表:即散列存储结构。 散列法存储的基本思想:建立关键码字与其存储位置的对应 关系,或者说,由关键码的值决定数据的存储地址。 优点:查找速度极快(O(1)),查找效率与元素个数n无关! 例1:若将学生信息按如下方式存入计算机,如: 将2001011810201的所有信息存入V[01]单元; 将2001011810202的所有信息存入V[02]单元; . 将2001011810231的所有信息存入V[31]单元。 欲查找学号为2001011810216的信息,便可直接访问V[16]!