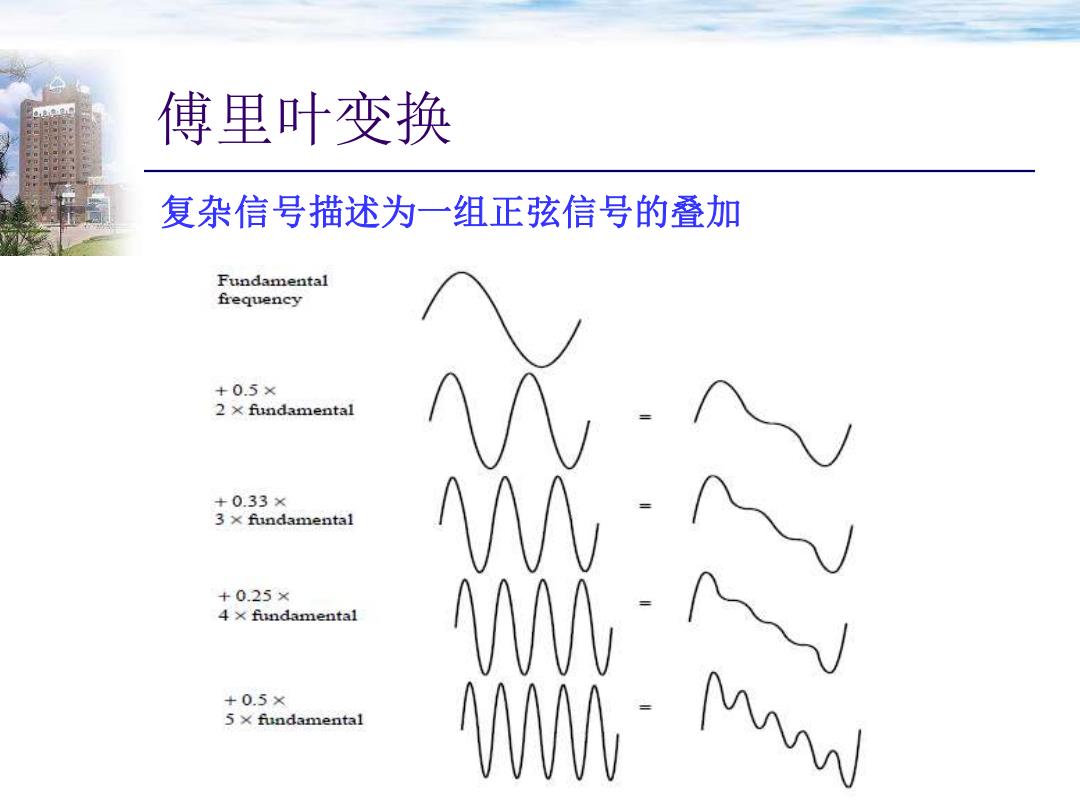
傅里叶变换 复杂信号描述为一组正弦信号的叠加 Fundamental frequency +0.5× 2×fundamental +0.33× 3×fundamenta1 N +0.25× 4 x fundamental +0.5× 5×fundamental
傅里叶变换 11 复杂信号描述为一组正弦信号的叠加
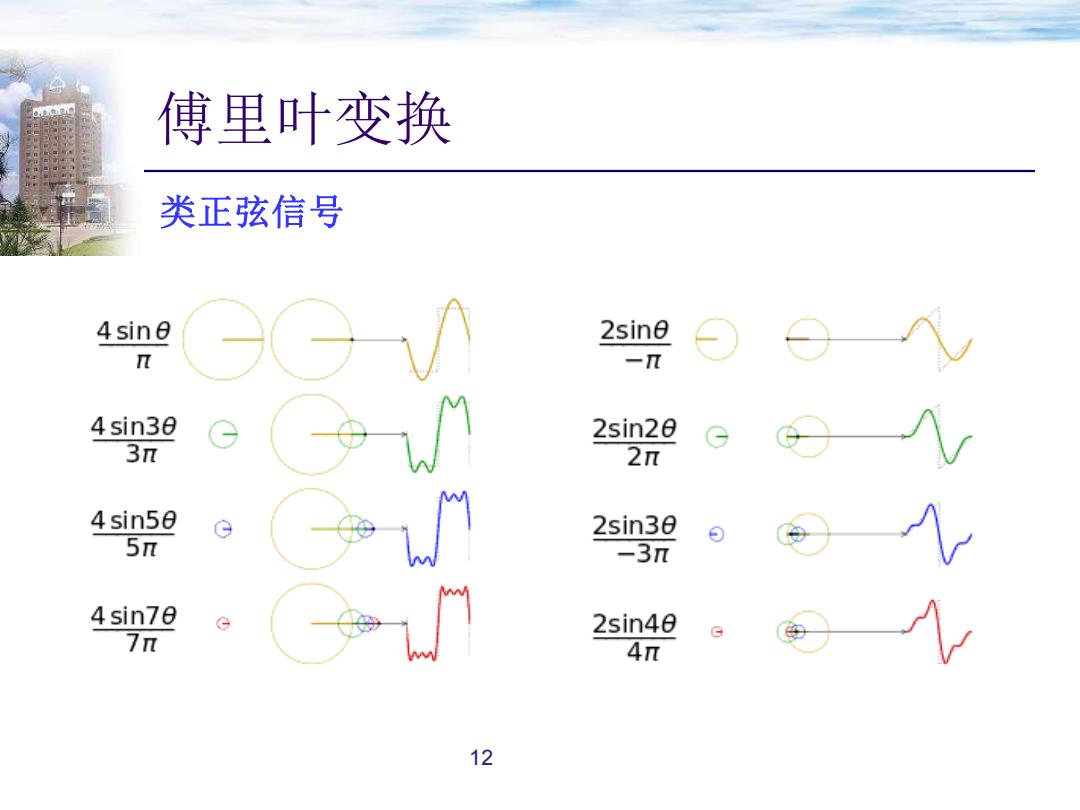
傅里叶变换 类正弦信号 4sin0 2sine π π 4sin30 2sin20 3π 2π 4 sin50 G 2sin30 5π -3π 4sin70 G 2sin40 7π G 4π 12
傅里叶变换 12 类正弦信号

傅里叶变换的基本原理 假设有一组单位正交基{ek} 则属于由单位正交基所构成空间内的向量可以描述为: v=>ak ek 其中,权重系数为 ak=v.ek Notes: ·每个向量可以被转换为一组权重系数 ·向量与权重系数之间的转换是可逆变换 13
傅里叶变换的基本原理 13 假设有一组单位正交基 则属于由单位正交基所构成空间内的向量可以描述为: 其中,权重系数为 Notes: • 每个向量可以被转换为一组权重系数 • 向量与权重系数之间的转换是可逆变换

函数的线性计算 向量的内积: ū.v=∑0 类比定义函数的内积: 1.g= f(x)g(x)dx Functions satisfy all of the linear algebraic requirements of vectors. 14
函数的线性计算 14 向量的内积: 类比定义函数的内积:

傅里叶变换的基本原理 类比向量的正交投影变换,函数同样满足: Vectors [ek} Functions {ek(t)} Transform ak=v.ek ak =f.ek =∑叨ek] f(t)ek(t)dt Inverse f(=∑ake( 15
傅里叶变换的基本原理 15 类比向量的正交投影变换,函数同样满足: