
第5章模拟调制系统 ◆相移法和$SB信号的时域表示 口SSB信号的时域表示式 设单频调制信号为m()=4 cos0mt 载波为c(t)=cos0,t 则DSB信号的时域表示式为 SpsB(1)=A cos@t cos@t -4 costo.++A costo.-) 若保留上边带,则有 两式仅正负号不同 5s(()cosc0s0 cossino. 若保留下边带,则有 Ss(cos(o-0co30.tcos014sino isinos 16
16 第5章 模拟调制系统 ◆ 相移法和SSB信号的时域表示 SSB信号的时域表示式 设单频调制信号为 载波为 则DSB信号的时域表示式为 若保留上边带,则有 若保留下边带,则有 m t A t m m ( ) = cos c t t c ( ) = cos A t A t s t A t t m c m m c m DSB m m c cos( ) 2 1 cos( ) 2 1 ( ) cos cos = + + − = 1 ( ) cos( ) 2 USB m C m s t A t = + 1 1 cos cos sin sin 2 2 = − A t A t m m c m m c 1 ( ) cos( ) 2 LSB m C m s t A t = − 1 1 cos cos sin sin 2 2 = + A t t A t t m m c m m c 两式仅正负号不同

第5章模拟调制系统 将上两式合并: s(.co.com 式中,”-”表示上边带信号,"+”表示下边带信号。 希尔伯特变换:上式中4m sin@m可以看作是4m cosont相移 π/2的结果。把这一相移过程称为希尔伯特变换,记为 ”A”,则有 A cosot=A sin @t 这样,上式可以改写为 s()-co0sino. 17
17 第5章 模拟调制系统 将上两式合并: 式中,“-”表示上边带信号,“+”表示下边带信号。 希尔伯特变换:上式中Am sinmt可以看作是Am cosmt 相移 /2的结果。把这一相移过程称为希尔伯特变换,记为 “ ^ ”,则有 这样,上式可以改写为 s t A t t A t t SSB m m c m m c sin sin 2 1 cos cos 2 1 ( ) = A t A t m m m m co ˆ s = sin 1 1 ( ) cos cos cos sin 2 2 SSB m m c m m c s t A t t A t t =

第5章模拟调制系统 Saa()co.tcocosinm. 把上式推广到一般情况,则得到 sssa()-(s.sin 式中,mt)是mt)的希尔伯特变换 若M(o)是m(t)的傅里叶变换,则m(t)的傅里叶变换M(o)为 M(o)=M(o)·[jsgn o] 式中 1, 0>0 sgn@= -1, 0<0 上式中的[-jsgn@]可以看作是希尔伯特滤波器传递函数,即 H(@)=M(@)/M(@)=-jsgn@ 18
18 第5章 模拟调制系统 把上式推广到一般情况,则得到 式中, 若M()是m(t)的傅里叶变换,则 式中 上式中的[-jsgn]可以看作是希尔伯特滤波器传递函数,即 1 1 ( ) cos cos cos sin 2 2 SSB m m c m m c s t A t t A t t = s t m t t m t t SSB c c ˆ( )sin 2 1 ( ) cos 2 1 ( ) = m ˆ(t)是m(t)的希尔伯特变换m ˆ(t)的傅里叶变换M ˆ ()为 () () sgn ˆ M = M − j 1, 0 sgn 1, 0 = − Hh () = M ˆ ()/ M() = − jsgn

希尔伯特变换: 将一个信号)的全部频率分量相移90°后 所得的时间信号就叫做原信号的希尔波特变换 ),信号和它的希尔伯特变换互为正交。 正变换: 00 t-T d 逆变换: -00 f-t 频谱关系:弃(a)-jsgn(四)F() 19
19 希尔伯特变换: 将一个信号 f(t) 的全部频率分量相移-90°后 所得的时间信号就叫做原信号的希尔波特变换 ,信号和它的希尔伯特变换互为正交。 正变换: 逆变换: 频谱关系:
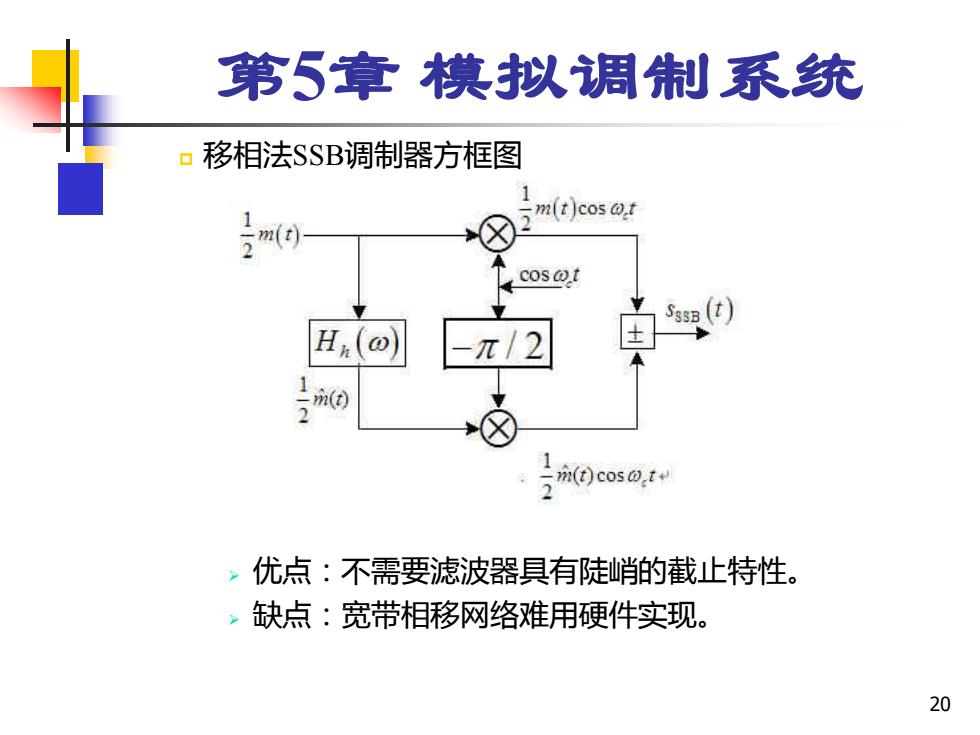
第5章模拟调制系统 口移相法SSB调制器方框图 m(t)cos@t cos @t s(t) Hx(@) -π/2 m(t)cos@.t ,优点:不需要滤波器具有陡峭的截止特性。 ,缺点:宽带相移网络难用硬件实现。 20
20 第5章 模拟调制系统 移相法SSB调制器方框图 ➢ 优点:不需要滤波器具有陡峭的截止特性。 ➢ 缺点:宽带相移网络难用硬件实现