
①KMP算法设计思想: (参见教材P80-84) 尽量利用已经部分匹配的结果信息,尽量让不要回溯,加快模式 串的滑动速度。 例:i S='a ba bc a bc a cb a b' S-'a babc a bc a c b a b' T=abc a c' T=abca c' S=a/babca bc a c b a b' i-T[O] Index_kmpl的返回值应为 i=6 需要讨论两个问题: ①如何由当前部分匹配结果确定模式向右滑动的新比较起点k? ②模式应该向右滑多远才是高效率的? 6
6 尽量利用已经部分匹配的结果信息,尽量让i不要回溯,加快模式 串的滑动速度。 例: ① KMP算法设计思想: (参见教材P80-84) S=‘a b a b c a b c a c b a b’ T=‘a b c a c’ S=‘a b a b c a b c a c b a b’ T=‘a b c a c’ S=‘a b a b c a b c a c b a b’ T=‘a b c a c’ Index_kmp的返回值应为 i=6 需要讨论两个问题: ①如何由当前部分匹配结果确定模式向右滑动的新比较起点k? ② 模式应该向右滑多远才是高效率的? i i i k k a b a a b c k i i i-T[0]
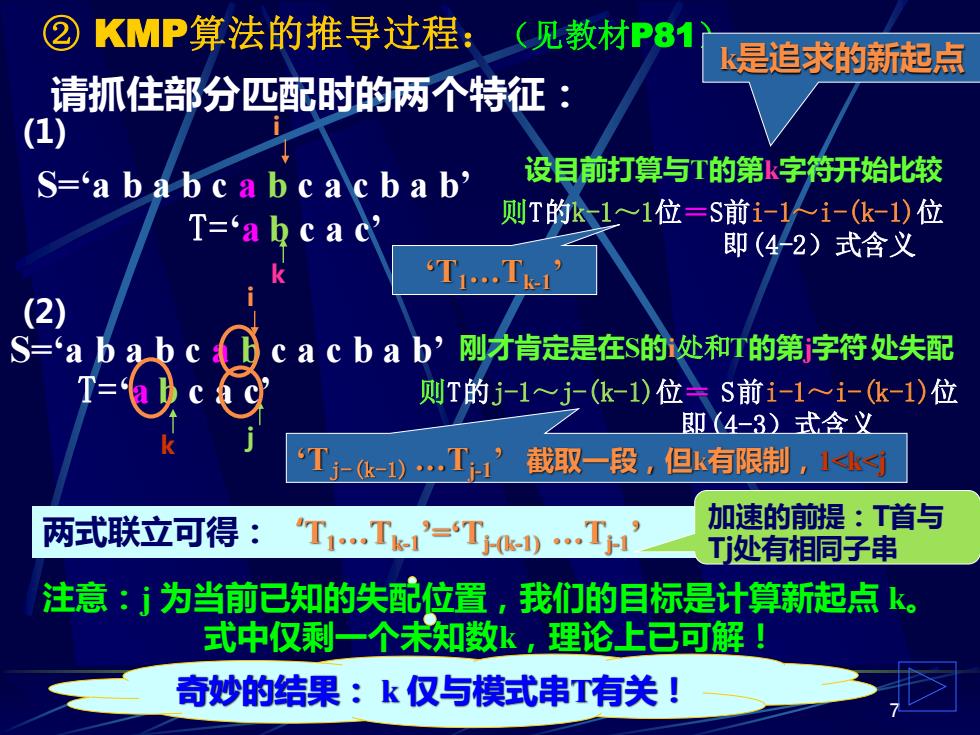
②KMP算法的推导过程: (见教材P81 k是追求的新起点 请抓住部分匹配时的两个特征: (1) S=a babc a b c a c b a b' 设目前打算与T的第k字符开始比较 T=‘a bc a c 则T的k-1~1位=S前i-1i-(k-1)位 即(42)式含义 T. (2) S=‘ababcbcacbab’刚才肯定是在s的处和r的第字符处失配 0c 则T的j-1j-(k-1)位S前i-1~i-k-1)位 即(4-3)式含义 TT’截取一段,但k有限制,1k 两式联立可得:TT’=T)Ti 加速的前提:T首与 Tj处有相同子串 注意:j为当前已知的失配位置,我们的目标是计算新起点k。 式中仅剩一个未知数k,理论上已可解! 奇妙的结果:k仅与模式串T有关!
奇妙的结果: 7 k 仅与模式串T有关! ② KMP算法的推导过程:(见教材P81) 请抓住部分匹配时的两个特征: 两式联立可得:‘T1.Tk-1 ’=‘Tj-(k-1) .Tj-1 ’ S=‘a b a b c a b c a c b a b’ T=‘a b c a c’ i k 则T的k-1~1位=S前i-1~i-(k-1)位 即(4-2)式含义 设目前打算与T的第k字符开始比较 (1) (2) ‘T1.Tk-1 ’ 则T的j-1~j-(k-1)位= S前i-1~i-(k-1)位 即(4-3)式含义 i k j S=‘a b a b c a b c a c b a b’ T=‘a b c a c’ 刚才肯定是在S的i处和T的第j字符处失配 ‘Tj-(k-1) .Tj-1 ’ 截取一段,但k有限制,1<k<j k是追求的新起点 加速的前提:T首与 Tj处有相同子串 注意:j 为当前已知的失配位置,我们的目标是计算新起点 k。 式中仅剩一个未知数k,理论上已可解!