text T a b a b a a b a b a =3 pattern P b a a Algorithm Preprocessing time Matching time Naive 0 O(n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m) Finite automaton O(1m∑) Θ(n) Knuth-Morris-Pratt Θ(1m) Θ(n) n:the length of text T m:the length of pattern the alphabet set,consisiting ofall possible characters
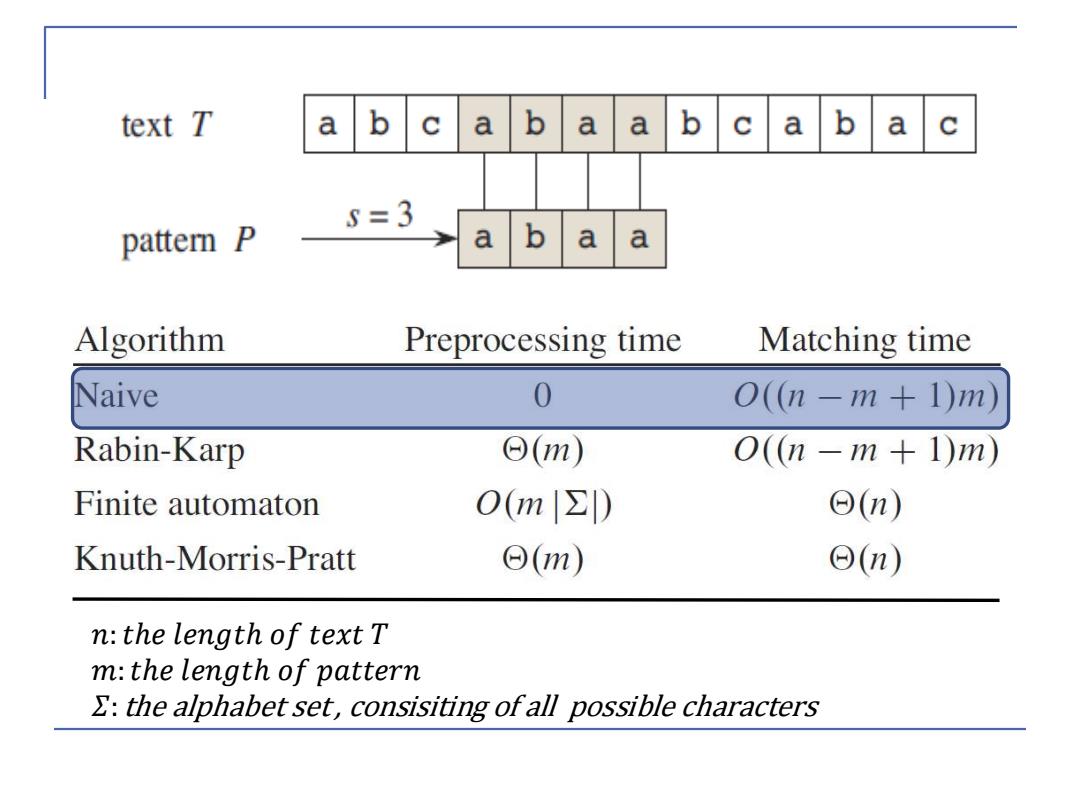
𝑛:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡𝑒𝑥𝑡 𝑇 𝑚:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑝𝑎𝑡𝑡𝑒𝑟𝑛 𝛴:the alphabet set , consisiting of all possible characters

最容易想到的算法 a a a b a a a b a a a b a a a b s=0 5=3 a a b b a a b NAIVE-STRING-MATCHER(T.P) 问题2: 1 n T.length 2 m =P.length 最坏情况下复杂度? 3 fors 0to n-m 0(n-m+1)m) 4 if P[1..ml==T[s +1..s+ml 5 print"Pattern occurs with shift"s 问题3:什么时候出现最坏情况?
最容易想到的算法 𝑶 𝒏 − 𝒎 + 𝟏 𝒎

问题4:你能否说说naive.算法有什么问 题,为什么有可能改进? a a b a a a a b S=0 S=3 a a b a a b NAIVE-STRING-MATCHER(T,P) 逐位单字符比较 1 n T.length The naive string-matcher is 2 m P.length inefficient because it entirely 3 fors 0to n-m ignores information gained if P[1..m ==Ts +1..s+m about the text for one value print“Pattern occurs with shift”s of s when it considers other values of s
The naive string-matcher is inefficient because it entirely ignores information gained about the text for one value of s when it considers other values of s

text T a b a b a a b a b a =3 pattern P b a a Algorithm Preprocessing time Matching time Naive 0 O(n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m) Finite automaton O(m∑) ⊙(n) Knuth-Morris-Pratt Θ(1m) ©(n) n:the length of text T m:the length of pattern the alphabet set,consisiting ofall possible characters
𝑛:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡𝑒𝑥𝑡 𝑇 𝑚:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑝𝑎𝑡𝑡𝑒𝑟𝑛 𝛴:the alphabet set , consisiting of all possible characters

问题5: Rabin-Karp算法的基本思想 是什么? For expository purposes,let us assume that∑={0,1,2,.,9},so that each character is a decimal digit.(In the general case,we can assume that each charac- ter is a digit in radix-d notation,where d=We can then view a string ofk consecutive characters as representing a length-k decimal number.The character string 31415 thus corresponds to the decimal number 31,415
问题5: Rabin-Karp算法的基本思想 是什么?