
Thinking 1.热力学基本关系式dH=TdS+VdP只适用于可逆过程。 (错。不需要可逆条件,适用于只有体积功存在的封闭体系) 2.象dU=TdS-PdV等热力学基本方程只能用于气体,而不能用于液体或固相。 (错。能用于任何相态) 3.对于一均匀的物质,其H和U的关系为 A H<U BH>U C H=U D不能确定 (B。因H=U+PV)
(错。能用于任何相态) Thinking 1. 热力学基本关系式dH=TdS+VdP只适用于可逆过程。 (错。不需要可逆条件,适用于只有体积功存在的封闭体系) 2. 象dU=TdS-PdV等热力学基本方程只能用于气体,而不能用于液体或固相。 3. 对于一均匀的物质,其H和U的关系为 A H<U B H>U C H=U D 不能确定 (B。因H=U+PV)

4.某人声明所建立的纯固体的状态方程和热力学能的方程分别为 V='-aP+bT和U=cT-bPT 其中,a、b、c和V为常数,试从热力学上证明这两个方程的可靠性。 解:由基本关系式和Maxwell关系式 dU TdS-Pdv dH TdS +VdP dA=-PdV-SdT dG =VdP-SdT (av/op),a ”P=%-V+bt 部)-(s) a )-P=br-%-V+b7=-+y a 0 a ().-() 由此可以得到 V=Vo +bT 8 -( (这种体积关系一般能成立,故方程有一定的可靠性)
0 和 −=+−= bPTcTUbTaPVV 4.某人声明所建立的纯固体的状态方程和热力学能的方程分别为 其中, a 、 b 、 c 和 V0为常数,试从热力学上证明这两个方程的可靠性。 解:由基本关系式和 Maxwell关系式 P T P T V U T V ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ( ) ( ) T T U b U P T V VP a ∂ ∂ ∂ = = ∂ ∂∂ ( ) T a bTVV P +− = 0 0 0 V P b V V bT V V T PT Taa a ⎛ ⎞ ∂ − + −+ ⎜ ⎟ −= − = ⎝ ⎠ ∂ dA dU dH TdS Vd dG VdP P S d dT V TdS PdV SdT P = = − − = − = + − 0 += bTVV (这种体积关系一般能成立,故方程有一定的可靠性)。 由此可以得到 S P T V T S P V P S V S T P T V P S V P V S T T ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ = − ⎛⎞⎛ ⎞ ⎜⎟⎜ ⎟ = ⎝⎠⎝ ∂ ∂ ⎜ ⎟ ⎜⎟ ⎝ ⎠ ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ⎜ ⎟ ⎜⎟ = − ⎝ ∂ ∂ ⎛ ⎞⎛ ⎞ ∂ ∂ ⎜ ⎟⎜ ⎟ = ∂ ∂ ⎠ ⎝ ⎝ ⎠ ⎝ ⎠ ⎠ ⎠ ⎠ ⎝

6.1.4 Application of Maxwell's Equation Maxwell关系式的应用) For a single phase and single component f=C-P+2=1-1+2=2 That is the thermodynamic state function can be calculated by two variables only For example U=U(T,V)U=U,(P,T)U=U3(P,V) etc
6.1.4 Application of Maxwell’s Equation (Maxwell关系式的应用 ) For a single phase and single component f = C-P+2 = 1-1+2=2 That is : the thermodynamic state function can be calculated by two variables only For example U=U 1 (T,V) U=U 2 (P,T) U=U 3 (P,V) etc
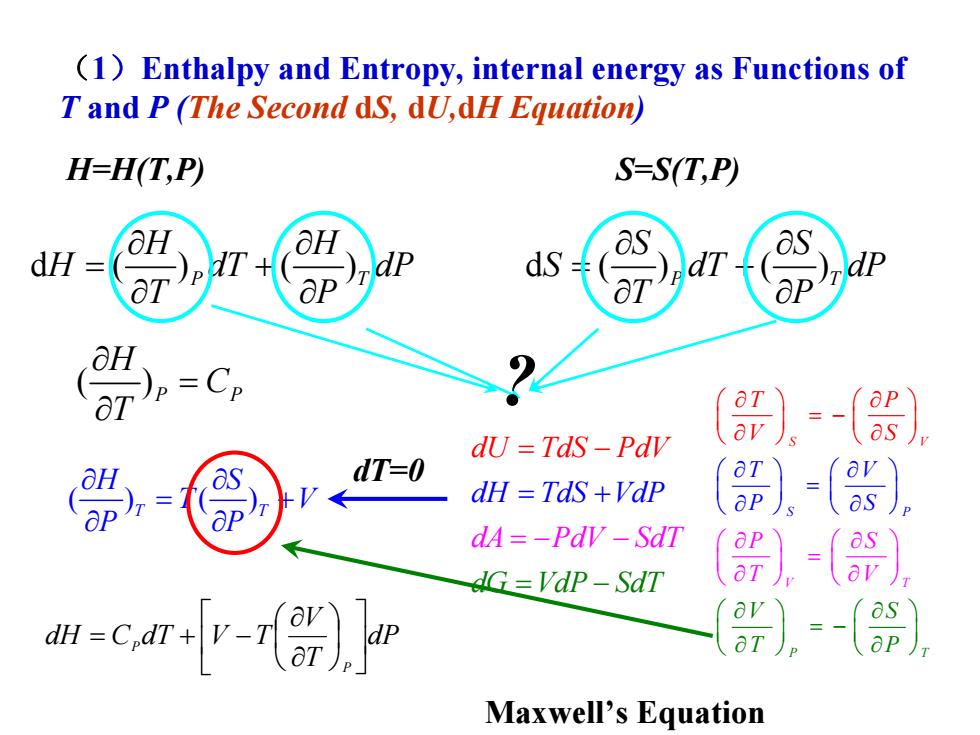
(1)Enthalpy and Entropy,internal energy as Functions of T and P(The Second ds,dU,dH Equation) H=H(T,P) S=S(T,P) dH ID dU TdS-Pdv dT-0 dH TdS+VdP dA=-PdV-SdT dG=VdP-SdT 8).-() m-cmv-)r Maxwell's Equation
S P T V T S P V P S V S T P T V P S V P V S T T ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ = − ⎛⎞⎛ ⎞ ⎜⎟⎜ ⎟ = ⎝⎠⎝ ∂ ∂ ⎜ ⎟ ⎜⎟ ⎝ ⎠ ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ⎜ ⎟ ⎜⎟ = − ⎝ ∂ ∂ ⎛ ⎞⎛ ⎞ ∂ ∂ ⎜ ⎟⎜ ⎟ = ∂ ∂ ⎠ ⎝ ⎝ ⎠ ⎝ ⎠ ⎠ ⎠ ⎠ ⎝ (1)Enthalpy and Entropy, internal energy as Functions of T and P (The Second dS, dU,dH Equation) H=H(T,P) S=S(T,P) d () () P T H H H dT dP T P ∂ ∂ = + ∂ ∂ d () () P T S S S dT dP T P ∂ ∂ = + ∂ ∂ ( )P P ? H C T∂ = ∂ dT=0 dA dU dH TdS Vd dG VdP P S d dT V TdS PdV SdT P = = − − = − = + − ( ) () T T H S T V P P ∂ ∂ = + ∂ ∂ dP T V TVdTCdH P P ⎥⎦⎤ ⎢⎣⎡ ⎟⎠⎞ ⎜⎝⎛ ∂∂ −+= Maxwell’s Equation

H=H(T,P) S-S(T,P) S dH dS D =U as () ap av d= dp av S-S=△S= dp
S P T V T S P V P S V S T P T V P S V P V S T T ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ = − ⎛⎞⎛ ⎞ ⎜⎟⎜ ⎟ = ⎝⎠⎝ ∂ ∂ ⎜ ⎟ ⎜⎟ ⎝ ⎠ ∂ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ⎜ ⎟ ⎜⎟ = − ⎝ ∂ ∂ ⎛ ⎞⎛ ⎞ ∂ ∂ ⎜ ⎟⎜ ⎟ = ∂ ∂ ⎠ ⎝ ⎝ ⎠ ⎝ ⎠ ⎠ ⎠ ⎠ ⎝ H=H(T,P) S=S(T,P) d () () P T H H H dT dP T P ∂ ∂ = + ∂ ∂ d () () P T S S S dT dP T P ∂ ∂ = + ∂ ∂ ( )P P ? H C T ∂ = ∂ dA dU dH TdS Vd dG VdP P S d dT V TdS PdV SdT P = = − − = − = + − ( ) () T T H S T V P P ∂ ∂ = + ∂ ∂ dP T V TVdTCdH P P ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ −+= dP=0 ( ) () ( ) P P P P H S T T T S C T T ∂ ∂ = ∂ ∂ ∂ = ∂ P T V S T P ⎛ ⎞ ⎛⎞ ∂ ∂ ⎜ ⎟ ⎜⎟ = − ⎝ ⎠ ⎝⎠ ∂ ∂ dP T V dT T C dS P P ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ −=