
第10卷第2期 智能系统学报 Vol.10 No.2 2015年4月 CAAI Transactions on Intelligent Systems Apr.2015 D0:10.3969/j.issn.1673-4785.201402019 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20150326.1016.004.html 动态调整策略改进的和声搜索算法 拓守恒,雍龙泉,邓方安 (陕西理工学院数计学院,陕西汉中723001) 摘要:为了得到高维复杂问题的全局高精度最优解,提出一种动态调整策略,并用该策略改进和声搜索算法。算 法选取和声记忆库中最差和声向量作为优化调整目标,随着迭代的进行,逐步降低决策变量的调整概率,该方法能 够使得算法在全局探索能力和局部高精度开发能力之间实现平衡,有效提高了新和声更新最差和声的成功率。通 过6个高维Benchmark测试函数的仿真结果表明,提出的动态调整策略能够有效提高和声搜索算法求解高维复杂优 化问题的能力。 关键词:自适应调整策略:高维优化问题:和声搜索算法 中图分类号:TP391文献标志码:A文章编号:1673-4785(2015)02-0307-09 中文引用格式:拓守恒,雍龙泉,邓方安.动态调整策略改进的和声搜索算法[J].智能系统学报,2015,10(2):307315. 英文引用格式:TUO Shouheng,YONG Longquan,DENG Fang'an.Dynamic adjustment strategy for improving the harmony search algorithm[J].CAAI Transactions on Intelligent Systems,2015,10(2):307-315. Dynamic adjustment strategy for improving the harmony search algorithm TUO Shouheng,YONG Longquan,DENG Fang'an (School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong 723001,China) Abstract:A dynamic adjustment strategy is used to improve the harmony search algorithm for solving high-dimen- sional multimodal global optimization problems.It chooses the worst harmony vector from the harmony memory (HM)as an optimization objective vector.With the process of iteration,the adjustment probability of decision vari- ables is reduced step by step.It can achieve the balance effectively between the global exploration powers and local exploitation competence,and can increase the success rate of evolution.Finally,the experimental results of 16 high-dimension benchmark functions demonstrated that the proposed method can enhance the performance and ro- bustness of the harmony search algorithm obviously in solving large scale multimodal optimization problems. Keywords:adaptive adjustment strategy;high-dimensional optimization problems;harmony search algorithm 近年来,随着社会的发展和大数据时代的到来,年来,研究者将关注的焦点集中在模拟自然的启发 人们对科技产品的能耗和性能要求越来越高,使得 式(meta-heuristics)优化方法[1]等。 产品的设计遇到了极大的挑战。许多产品的设计需 和声搜索算法是Geem等[1]在2001年通过模 要考虑很多的设计要求,并要使其产品整体设计能 拟音乐家创作音乐和调节和声的过程,提出的一种 够达到最优,这些问题都可转化为大规模复杂优化 新的启发式优化算法。音乐家在音乐创作过程中, 问题(optimization problems,OP)。对于OP问题,近 需要不断调整各个音符,使其成为优美和声。由于 和声算法搜索能力强,并且结构简单,很容易在各种 收稿日期:2014-02-21.网络出版日期:2015-03-26. 基金项目:国家自然科学基金资助项目(11401357),陕西省教育厅科研软件和硬件中实现,引起很多科学研究者和工程设 资助项目(14K1141):汉中市科技局科研资助项目 (2013hz-39);陕西理工学院科研资助项目(SLGKY13-27) 计人员的关注,近年来,已经广泛应用于实践中,例 通信作者:拓守恒.tu0_sh@126.com. 如,管网优化设计[1]、结构优化设计11)、交通运输
第 10 卷第 2 期 智 能 系 统 学 报 Vol.10 №.2 2015 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2015 DOI:10.3969 / j.issn.1673⁃4785.201402019 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150326.1016.004.html 动态调整策略改进的和声搜索算法 拓守恒,雍龙泉,邓方安 (陕西理工学院 数计学院,陕西 汉中 723001) 摘 要:为了得到高维复杂问题的全局高精度最优解,提出一种动态调整策略,并用该策略改进和声搜索算法。 算 法选取和声记忆库中最差和声向量作为优化调整目标,随着迭代的进行,逐步降低决策变量的调整概率,该方法能 够使得算法在全局探索能力和局部高精度开发能力之间实现平衡,有效提高了新和声更新最差和声的成功率。 通 过 6 个高维 Benchmark 测试函数的仿真结果表明,提出的动态调整策略能够有效提高和声搜索算法求解高维复杂优 化问题的能力。 关键词:自适应调整策略;高维优化问题;和声搜索算法 中图分类号:TP391 文献标志码:A 文章编号:1673⁃4785(2015)02⁃0307⁃09 中文引用格式:拓守恒,雍龙泉,邓方安.动态调整策略改进的和声搜索算法[J]. 智能系统学报, 2015, 10(2): 307⁃315. 英文引用格式:TUO Shouheng, YONG Longquan, DENG Fang’ an. Dynamic adjustment strategy for improving the harmony search algorithm[J]. CAAI Transactions on Intelligent Systems, 2015, 10(2): 307⁃315. Dynamic adjustment strategy for improving the harmony search algorithm TUO Shouheng, YONG Longquan, DENG Fang’an (School of Mathematics and Computer Science, Shaanxi University of Technology, Hanzhong 723001,China) Abstract:A dynamic adjustment strategy is used to improve the harmony search algorithm for solving high⁃dimen⁃ sional multimodal global optimization problems. It chooses the worst harmony vector from the harmony memory (HM) as an optimization objective vector. With the process of iteration, the adjustment probability of decision vari⁃ ables is reduced step by step. It can achieve the balance effectively between the global exploration powers and local exploitation competence, and can increase the success rate of evolution. Finally, the experimental results of 16 high⁃dimension benchmark functions demonstrated that the proposed method can enhance the performance and ro⁃ bustness of the harmony search algorithm obviously in solving large scale multimodal optimization problems. Keywords:adaptive adjustment strategy; high⁃dimensional optimization problems; harmony search algorithm 收稿日期:2014⁃02⁃21. 网络出版日期:2015⁃03⁃26. 基金项目:国家自然科学基金资助项目(11401357),陕西省教育厅科研 资助 项 目 ( 14JK1141 ); 汉 中 市 科 技 局 科 研 资 助 项 目 (2013hzzx⁃39);陕西理工学院科研资助项目(SLGKY 13⁃27). 通信作者:拓守恒.tuo_sh@ 126.com. 近年来,随着社会的发展和大数据时代的到来, 人们对科技产品的能耗和性能要求越来越高,使得 产品的设计遇到了极大的挑战。 许多产品的设计需 要考虑很多的设计要求,并要使其产品整体设计能 够达到最优,这些问题都可转化为大规模复杂优化 问题(optimization problems,OP)。 对于 OP 问题,近 年来,研究者将关注的焦点集中在模拟自然的启发 式(meta⁃heuristics)优化方法[ 1⁃9 ]等。 和声搜索算法是 Geem 等[ 1 ] 在 2001 年通过模 拟音乐家创作音乐和调节和声的过程,提出的一种 新的启发式优化算法。 音乐家在音乐创作过程中, 需要不断调整各个音符,使其成为优美和声。 由于 和声算法搜索能力强,并且结构简单,很容易在各种 软件和硬件中实现,引起很多科学研究者和工程设 计人员的关注,近年来,已经广泛应用于实践中,例 如,管网优化设计[ 10 ] 、结构优化设计[ 11 ] 、交通运输

·308· 智能系统学报 第10卷 路径优化]、电力系统经济负荷分配问题13]和 BW)。各参数含义如下: PD控制器优化]等领域。然而,研究发现,在有 D为问题的维数,HMS为和声记忆库大小,Tm 限的时间内,和声搜索算法具有很强的全局探索能 为算法迭代次数:HMCR为和声记忆库选择概率, 力,但是,在实数优化问题中,求解精度较低[51。 PAR为局部微调概率,BW为局部微调步长值。 为此,很多改进的和声搜索算法被提出,潘全科 2)随机初始化和声记忆库HM 等[15]采用动态子种群策略提出了局部最好和声搜 =xL:+rand·(xU:-xL:) 索算法,利用自适应动态策略提出一种全局最优和 i=1,2,…,D:j=1,2,…,HMS 声搜索算法[i6]。M.Mahdavi等设计出一种参数动 式中:rand是(0,1)中的随机数。 态调整策略,有效改进了HS算法的性能(IHS)〔18]: 树 7 M.G.H.Omran提出全局最优和声搜索算法 x好 好 . 品 (GHS)【1];Zou[20]采用一种很简单的差分学习策 2 HM 略,有效屏蔽了参数HMCR(harmony memory con-- XHMS sidering rate)和PAR(pitch-adjusting rate),降低了 算法的复杂性21-]。P.Yadav给出一种智能调整和 3)利用3种和声调节规则创作新和声 声搜索算法(THS)[)]:S.Das通过理论分析与证 通过如下3个规则产生新和声xw= 明,给出了一种新的和声步长(pitch bandwidth,BW) [xxw…x8]。 调整算法(EHS)【);本文作者在文献[24]和[25] ①和声记忆库选择。新和声向量x"的决策变 中分别提出了“混沌和声搜索算法”与“基于教与学 量x"(i=1,2,…,D)以概率HMCR从和声记忆库 策略的和声搜索算法”:另外,在一些具体应用中, 的第i维[xx…xs]中随机选取。 对和声搜索算法进行了有效改进[263]。尽管上述 ②局部微调。局部微调是将①中产生的x 改进算法从某些方面对和声搜索算法进行了改进, (i=1,2,…,D)以概率PAR进行再次微调。微调 但并没有从算法的运行代价考虑,比如EHS算法, 方法如下: 虽然搜索能力有了明显的改进,但是,由于每次迭代 xew=xew±rand·BW(i) 都需要计算和声记忆库(harmony memory,HM)的方 ③搜索空间内随机产生。新和声向量x"的决 差,其计算量甚至超过了和声搜索算法本身的计算 策变量x(i=1,2,…,D)以概率1-HMCR在搜索 量,使得算法的运行代价是标准和声算法HS的好 空间内随机产生。产生方法如下: 几倍。特别是在求解高维复杂优化问题时,目前的 xM=xL rand.(xU:-xL) 和声算法运行速度普遍较慢。为此,本文通过引入 4)更新操作 一种动态和声调整策略,使其能够有效提高和声算 如果新和声向量x"优于HM中最差的和声 法的性能,并且,能使算法运行代价降低,提高其搜 x,则用x将其替换,否则,转至(3)重新产生新 索速度。 和声。重复3)、4),直到满足终止条件。 1 标准和声搜索算法 2动态降维和声调整策略 考虑如下优化问题: 2.12种和声调整策略分析与比较 minf八x),x=[x1x2xp] 目前的和声搜索算法和一些改进算法是在整个 s.t.x;E [xLi,xU:],i=1,2,....D 种群的基础上通过组合策略(规则①)产生新的候 式中:f(x)是目标函数,x是由D个决策变量x 选解,这样实现了组合算子的多样性,因此具有较好 (i=1,2,…,D)构成的解向量,[xL:,xU】表示决 的全局搜索性能。但是,在进化后期,即使发现了全 策变量x:的可行搜索区域.将该优化问题对应于和 局最优解所在的区域,由于其较低的更新成功率 声算法,x表示一个和声向量,f(x)表示和声x的 (更新成功率是指每次产生的新解好于和声记忆库 旋律优美程度(在该问题中,(x)越小,表示其和声 中最差解的概率),使得算法往往很难获得高精度 旋律越优美)。 的最优解。 1.1标准和声搜索算法 对于一个高维优化问题,必然要从大范围的扰 标准和声搜索算法的基本步骤如下: 动开始逐步到小范围(部分维度)的微调,最终使其 1)设置参数值(D,HMS,T,HMCR,PAR, 在所有维上都能够达到最优,然而,和声优化算法在
路径优化[ 12 ] 、电力系统经济负荷分配问题[ 13 ] 和 PID 控制器优化[14] 等领域。 然而,研究发现,在有 限的时间内,和声搜索算法具有很强的全局探索能 力,但是,在实数优化问题中,求解精度较低[ 15⁃17] 。 为此,很多改进的和声搜索算法被提出, 潘全科 等[ 15 ]采用动态子种群策略提出了局部最好和声搜 索算法,利用自适应动态策略提出一种全局最优和 声搜索算法[ 16 ] 。 M. Mahdavi 等设计出一种参数动 态调整策略,有效改进了 HS 算法的性能(IHS) [ 18 ] ; M. G. H. Omran 提 出 全 局 最 优 和 声 搜 索 算 法 (GHS) [ 19 ] ; Zou [20]采用一种很简单的差分学习策 略,有效屏蔽了参数 HMCR ( harmony memory con⁃ sidering rate )和 PAR( pitch⁃adjusting rate),降低了 算法的复杂性[ 21⁃22 ] 。 P.Yadav 给出一种智能调整和 声搜索算法( ITHS) [17] ; S.Das 通过理论分析与证 明,给出了一种新的和声步长(pitch bandwidth,BW) 调整算法(EHS) [ 23 ] ;本文作者在文献[24]和[25] 中分别提出了“混沌和声搜索算法”与“基于教与学 策略的和声搜索算法”;另外,在一些具体应用中, 对和声搜索算法进行了有效改进[26⁃34] 。 尽管上述 改进算法从某些方面对和声搜索算法进行了改进, 但并没有从算法的运行代价考虑,比如 EHS 算法, 虽然搜索能力有了明显的改进,但是,由于每次迭代 都需要计算和声记忆库(harmony memory,HM)的方 差,其计算量甚至超过了和声搜索算法本身的计算 量,使得算法的运行代价是标准和声算法 HS 的好 几倍。 特别是在求解高维复杂优化问题时,目前的 和声算法运行速度普遍较慢。 为此,本文通过引入 一种动态和声调整策略,使其能够有效提高和声算 法的性能,并且,能使算法运行代价降低,提高其搜 索速度。 1 标准和声搜索算法 考虑如下优化问题: min f(x),x = [x1 x2 … xD] s.t.xi ∈ xLi,xUi [ ] ,i = 1,2,…,D 式中: f(x) 是目标函数, x 是由 D 个决策变量 xi (i =1,2,…,D )构成的解向量, xLi,xUi [ ] 表示决 策变量 xi 的可行搜索区域. 将该优化问题对应于和 声算法, x 表示一个和声向量, f(x) 表示和声 x 的 旋律优美程度(在该问题中, f(x) 越小,表示其和声 旋律越优美)。 1.1 标准和声搜索算法 标准和声搜索算法的基本步骤如下: 1)设置参数值( D, HMS, Tmax, HMCR,PAR, BW)。 各参数含义如下: D 为问题的维数,HMS 为和声记忆库大小, Tmax 为算法迭代次数;HMCR 为和声记忆库选择概率, PAR 为局部微调概率,BW 为局部微调步长值。 2)随机初始化和声记忆库 HM x j i = xLi + rand·(xUi - xLi) i = 1,2,…,D;j = 1,2,…,HMS 式中:rand 是(0,1)中的随机数。 HM = x 1 x 2 ... x HMS é ë ê ê ê ê ê ù û ú ú ú ú ú = x 1 1 x 1 2 … x 1 D x 2 1 x 2 2 … x 2 D ︙ ︙ ︙ x HMS 1 x HMS 2 … x HMS D é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 3)利用 3 种和声调节规则创作新和声 通 过 如 下 3 个 规 则 产 生 新 和 声 x new = [x new 1 x new 2 … x new D ] 。 ①和声记忆库选择。 新和声向量 x new 的决策变 量 x new i (i = 1,2,…,D) 以概率 HMCR 从和声记忆库 的第 i 维 [x 1 i x 2 i … x HMS i ] T 中随机选取。 ②局部微调。 局部微调是将①中产生的 x new i (i =1,2,…,D) 以概率 PAR 进行再次微调。 微调 方法如下: x new i = x new i ± rand·BW(i) ③搜索空间内随机产生。 新和声向量 x new 的决 策变量 x new i (i = 1,2,…,D) 以概率 1⁃HMCR 在搜索 空间内随机产生。 产生方法如下: x new i = xLi + rand·(xUi - xLi) 4)更新操作 如果新和声向量 x new 优于 HM 中最差的和声 x worst ,则用 x new 将其替换,否则,转至(3)重新产生新 和声。 重复 3)、4),直到满足终止条件。 2 动态降维和声调整策略 2.1 2 种和声调整策略分析与比较 目前的和声搜索算法和一些改进算法是在整个 种群的基础上通过组合策略(规则①)产生新的候 选解,这样实现了组合算子的多样性,因此具有较好 的全局搜索性能。 但是,在进化后期,即使发现了全 局最优解所在的区域,由于其较低的更新成功率 (更新成功率是指每次产生的新解好于和声记忆库 中最差解的概率),使得算法往往很难获得高精度 的最优解。 对于一个高维优化问题,必然要从大范围的扰 动开始逐步到小范围(部分维度)的微调,最终使其 在所有维上都能够达到最优,然而,和声优化算法在 ·308· 智 能 系 统 学 报 第 10 卷
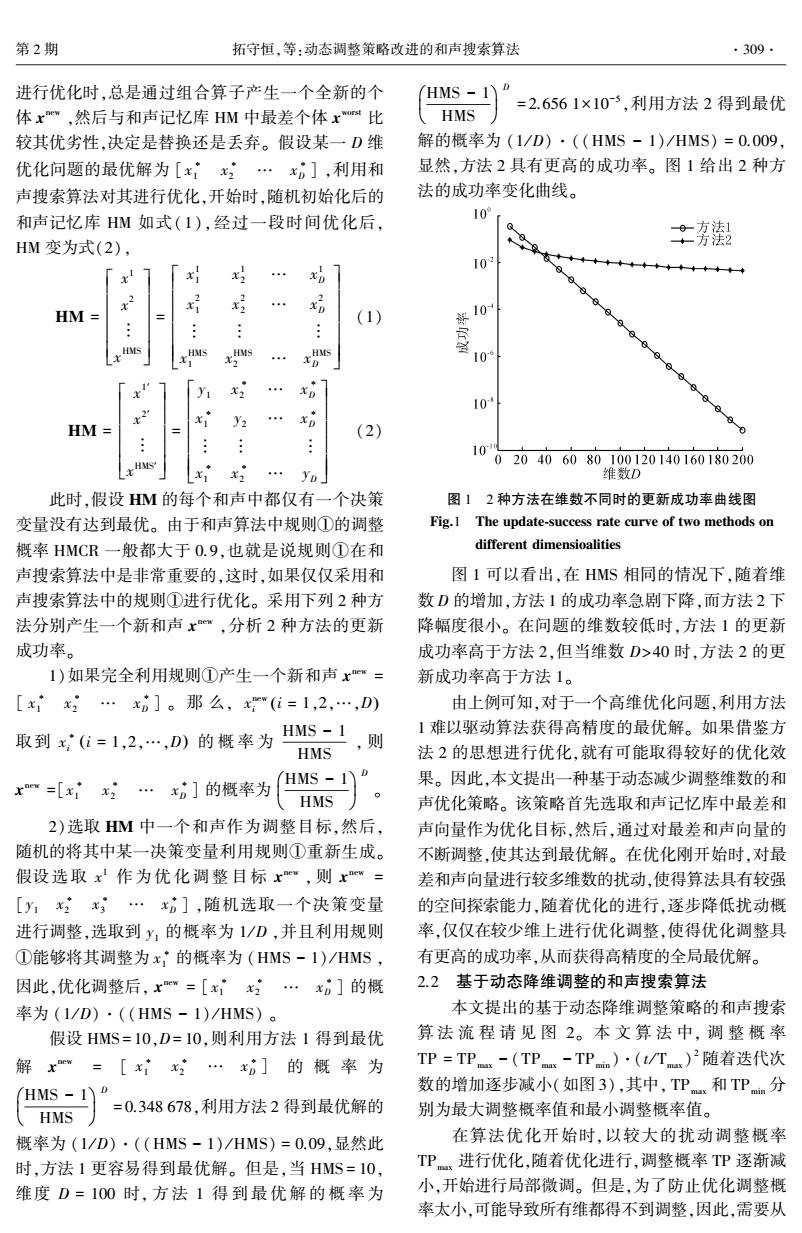
第2期 拓守恒,等:动态调整策略改进的和声搜索算法 ·309· 进行优化时,总是通过组合算子产生一个全新的个 HMS =2.6561×10-5,利用方法2得到最优 体x",然后与和声记忆库HM中最差个体x比 HMS 较其优劣性,决定是替换还是丢弃。假设某一D维 解的概率为(1/D)·((HMS-1)/HMS)=0.009, 优化问题的最优解为[xx…x],利用和 显然,方法2具有更高的成功率。图1给出2种方 声搜索算法对其进行优化,开始时,随机初始化后的 法的成功率变化曲线。 和声记忆库HM如式(1),经过一段时间优化后, 10 HM变为式(2), ·嘉潮 ◆ x 对 10 x好 HM (1) 10 109 y 10 x HM= 9 (2) 10 020406080100120140160180200 维数D 此时,假设HM的每个和声中都仅有一个决策 图12种方法在维数不同时的更新成功率曲线图 变量没有达到最优。由于和声算法中规则①的调整 Fig.1 The update-success rate curve of two methods on 概率HMCR一般都大于O.9,也就是说规则①在和 different dimensioalities 声搜索算法中是非常重要的,这时,如果仅仅采用和 图1可以看出,在HMS相同的情况下,随着维 声搜索算法中的规则①进行优化。采用下列2种方 数D的增加,方法1的成功率急剧下降,而方法2下 法分别产生一个新和声x,分析2种方法的更新 降幅度很小。在问题的维数较低时,方法1的更新 成功率。 成功率高于方法2,但当维数D>40时,方法2的更 1)如果完全利用规则①产生一个新和声x"= 新成功率高于方法1。 [x…x0]。那么,x"(i=1,2,…,D) 由上例可知,对于一个高维优化问题,利用方法 取到x(i=1,2,…,D)的概率为 HMS 1 ,则 1难以驱动算法获得高精度的最优解。如果借鉴方 HMS 法2的思想进行优化,就有可能取得较好的优化效 x=[xx…x]的概率为 HMS -1 果。因此,本文提出一种基于动态减少调整维数的和 HMS 声优化策略。该策略首先选取和声记忆库中最差和 2)选取HM中一个和声作为调整目标,然后, 声向量作为优化目标,然后,通过对最差和声向量的 随机的将其中某一决策变量利用规则①重新生成。 不断调整,使其达到最优解。在优化刚开始时,对最 假设选取x作为优化调整目标x",则xew= 差和声向量进行较多维数的扰动,使得算法具有较强 [y1x2x;…x。],随机选取一个决策变量 的空间探索能力,随着优化的进行,逐步降低扰动概 进行调整,选取到y1的概率为1/D,并且利用规则 率,仅仅在较少维上进行优化调整,使得优化调整具 ①能够将其调整为x的概率为(HMS-1)/HMS, 有更高的成功率,从而获得高精度的全局最优解。 因此,优化调整后,x=[xx…x0]的概 2.2基于动态降维调整的和声搜索算法 率为(1/D)·((HMS-1)/HMS)。 本文提出的基于动态降维调整策略的和声搜索 假设HMS=10,D=10,则利用方法1得到最优 算法流程请见图2。本文算法中,调整概率 解x=[xx…x门的概率为 TP=TP-(TP-TP)·(t/T)2随着迭代次 HMS -1 数的增加逐步减小(如图3),其中,TP和TPn分 、HMS =0.348678,利用方法2得到最优解的 别为最大调整概率值和最小调整概率值。 概率为(1/D)·((HMS-1)/HMS)=0.09,显然此 在算法优化开始时,以较大的扰动调整概率 时,方法1更容易得到最优解。但是,当HMS=10, TPx进行优化,随着优化进行,调整概率TP逐渐减 维度D=100时,方法1得到最优解的概率为 小,开始进行局部微调。但是,为了防止优化调整概 率太小,可能导致所有维都得不到调整,因此,需要从
进行优化时,总是通过组合算子产生一个全新的个 体 x new ,然后与和声记忆库 HM 中最差个体 x worst 比 较其优劣性,决定是替换还是丢弃。 假设某一 D 维 优化问题的最优解为 [x ∗ 1 x ∗ 2 … x ∗ D ] ,利用和 声搜索算法对其进行优化,开始时,随机初始化后的 和声记忆库 HM 如式(1),经过一段时间优化后, HM 变为式(2), HM = x 1 x 2 ︙ x HMS é ë ê ê ê ê ê ù û ú ú ú ú ú = x 1 1 x 1 2 … x 1 D x 2 1 x 2 2 … x 2 D ︙ ︙ ︙ x HMS 1 x HMS 2 … x HMS D é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (1) HM = x 1′ x 2′ ︙ x HMS′ é ë ê ê ê ê ê ù û ú ú ú ú ú = y1 x ∗ 2 … x ∗ D x ∗ 1 y2 … x ∗ D ︙ ︙ ︙ x ∗ 1 x ∗ 2 … yD é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (2) 此时,假设 HM 的每个和声中都仅有一个决策 变量没有达到最优。 由于和声算法中规则①的调整 概率 HMCR 一般都大于 0.9,也就是说规则①在和 声搜索算法中是非常重要的,这时,如果仅仅采用和 声搜索算法中的规则①进行优化。 采用下列 2 种方 法分别产生一个新和声 x new ,分析 2 种方法的更新 成功率。 1)如果完全利用规则①产生一个新和声 x new = [ x ∗ 1 x ∗ 2 … x ∗ D ] 。 那 么, x new i (i = 1,2,…,D) 取到 x ∗ i (i = 1,2,…,D) 的 概 率 为 HMS - 1 HMS , 则 x new =[x ∗ 1 x ∗ 2 … x ∗ D ] 的概率为 HMS - 1 HMS æ è ç ö ø ÷ D 。 2)选取 HM 中一个和声作为调整目标,然后, 随机的将其中某一决策变量利用规则①重新生成。 假设选取 x 1 作为优化 调 整 目 标 x new , 则 x new = [y1 x ∗ 2 x ∗ 3 … x ∗ D ] ,随机选取一个决策变量 进行调整,选取到 y1 的概率为 1 / D ,并且利用规则 ①能够将其调整为 x ∗ 1 的概率为 (HMS - 1) / HMS , 因此,优化调整后, x new = [ x ∗ 1 x ∗ 2 … x ∗ D ] 的概 率为 (1 / D)·((HMS - 1) / HMS) 。 假设 HMS = 10,D= 10,则利用方法 1 得到最优 解 x new = [ x ∗ 1 x ∗ 2 … x ∗ D ] 的 概 率 为 HMS - 1 HMS æ è ç ö ø ÷ D = 0.348 678,利用方法 2 得到最优解的 概率为 (1 / D)·((HMS - 1) / HMS) = 0.09,显然此 时,方法 1 更容易得到最优解。 但是,当 HMS = 10, 维度 D = 100 时, 方 法 1 得 到 最 优 解 的 概 率 为 HMS - 1 HMS æ è ç ö ø ÷ D = 2.656 1×10 -5 ,利用方法 2 得到最优 解的概率为 (1 / D)·((HMS - 1) / HMS) = 0.009, 显然,方法 2 具有更高的成功率。 图 1 给出 2 种方 法的成功率变化曲线。 图 1 2 种方法在维数不同时的更新成功率曲线图 Fig.1 The update⁃success rate curve of two methods on different dimensioalities 图 1 可以看出,在 HMS 相同的情况下,随着维 数 D 的增加,方法 1 的成功率急剧下降,而方法 2 下 降幅度很小。 在问题的维数较低时,方法 1 的更新 成功率高于方法 2,但当维数 D>40 时,方法 2 的更 新成功率高于方法 1。 由上例可知,对于一个高维优化问题,利用方法 1 难以驱动算法获得高精度的最优解。 如果借鉴方 法 2 的思想进行优化,就有可能取得较好的优化效 果。 因此,本文提出一种基于动态减少调整维数的和 声优化策略。 该策略首先选取和声记忆库中最差和 声向量作为优化目标,然后,通过对最差和声向量的 不断调整,使其达到最优解。 在优化刚开始时,对最 差和声向量进行较多维数的扰动,使得算法具有较强 的空间探索能力,随着优化的进行,逐步降低扰动概 率,仅仅在较少维上进行优化调整,使得优化调整具 有更高的成功率,从而获得高精度的全局最优解。 2.2 基于动态降维调整的和声搜索算法 本文提出的基于动态降维调整策略的和声搜索 算 法 流 程 请 见 图 2。 本 文 算 法 中, 调 整 概 率 TP = TP max - (TP max - TP min )·(t / Tmax) 2 随着迭代次 数的增加逐步减小(如图 3),其中, TP max 和 TP min 分 别为最大调整概率值和最小调整概率值。 在算法优化开始时,以较大的扰动调整概率 TPmax 进行优化,随着优化进行,调整概率 TP 逐渐减 小,开始进行局部微调。 但是,为了防止优化调整概 率太小,可能导致所有维都得不到调整,因此,需要从 第 2 期 拓守恒,等:动态调整策略改进的和声搜索算法 ·309·

310. 智能系统学报 第10卷 1~D中随机选取一维J=ceil(rand×D),使其必须得 0.50P 到调整,避免了算法“空转”。这样调整的好处是,迭 0.40 代初期,需要较强的全局扰动能力,此时,可以在优化 目标向量x"上加大扰动力度,增强种群多样性,使 要0叫 其具有较强的全局探索能力,随着优化的进行,到了 0.20 后期,多数个体可能已经聚集在了全局最优解附近, 0.1 10 此时,开始加强局部最优解的探索,为了保证较高的 012345678910 更新成功率,对优化目标向量x",选择较少的维数 迭代次数 进行优化调整,从而,增强算法的求解精度。 图3调整概率TP变化曲线 Fig.3 Adjustment curve of TP 开始○ TP=TPk一(TPat-TPm)×(t/T)2 3 仿真实验 从和声记忆库HM选择最差和声作为优化目标:x"=x© 为了评估本文算法提出的动态降维调整策略的 i=1 性能,选取了6个复杂的Benchmark测试函数进行仿 J=ceil(randxD) 真测试[6](见表1),16个函数除了F,和F。是单峰 函数之外,其余函数都是复杂的高维多峰值函数。 rand<TP Y 分别将HS,IHS、ITHS、EHS和GHS利用本文算 利用和声搜索算法在第维上产生一个新值作为x 法思想进行改进,将其改进后分别称为HS2,HS2, ITHS2,EHS2和GHS2,并将其与改进前的算法进行 i≤D 比较。检验改进后的算法是否比改进前的算法能够 N 获得更高精度的解,同时,检验其运行成本(运行时 执行更新操作 间)是否降低。 1+I 3.1实验环境和算法参数设置 K-Tmax 本文实验采用戴尔工作站T7500 Inter(R)Xe N on(R)CPUE560@2.1GHz,8.0GB内存,Windows End Server20O3 Server操作系统,所有测试程序采用Mat- 图2基于动态降维调整的和声搜索算法流程图 labR2009a编写。10种算法参数设置如表2。 Fig.2 The flow chart of HS algorithm based on dy- namic dimensionality reduction strategy 表16个Benchmark函数(F,~F。) Table 1 Six Benchmark functions 函数名称 Benchmark函数表达式 搜索范围 参数值 F Ackley x"=(0.0,…,0) Function F(x)=-20e-2-+20-e [-15,30]0 F(x)=0 F2Griewank x°=(0,0,…,0) [-600,600]P Function F2(x')=0 -1 F,(x)=sin2(my)+】 F;Levy 【-1)0+10im(,+)]+ x”=(1,1,…,1) (-1)2(1+10sin2(2myn) [-10,10]0 Function F(x)=0 y=1+(x-1)/4,i=1,2,…,D FMichalewics 乞ms)en(xya)产m:10 n=5 F(x)=- [-10,π]P Function F.(x)=-4.687658 F;Rastrigin x=(0,0,…,0) F,(x)=10D+ -10a(2》 [-5.12,5.12] Function F(x)=0 x·=(420.9687, F.Schwefel F(x)=418.9829D+ 2.26 Function 乞isin(V小国T) [-512,512]P420.9687,…,420.9687) F。(x)=0
1~D 中随机选取一维 J = ceil(rand×D) ,使其必须得 到调整,避免了算法“空转”。 这样调整的好处是,迭 代初期,需要较强的全局扰动能力,此时,可以在优化 目标向量 x new 上加大扰动力度,增强种群多样性,使 其具有较强的全局探索能力,随着优化的进行,到了 后期,多数个体可能已经聚集在了全局最优解附近, 此时,开始加强局部最优解的探索,为了保证较高的 更新成功率,对优化目标向量 x new ,选择较少的维数 进行优化调整,从而,增强算法的求解精度。 图 2 基于动态降维调整的和声搜索算法流程图 Fig.2 The flow chart of HS algorithm based on dy⁃ namic dimensionality reduction strategy 图 3 调整概率 TP 变化曲线 Fig.3 Adjustment curve of TP 3 仿真实验 为了评估本文算法提出的动态降维调整策略的 性能,选取了 6 个复杂的 Benchmark 测试函数进行仿 真测试[ 35⁃38 ] (见表 1),16 个函数除了 F7 和 F8 是单峰 函数之外,其余函数都是复杂的高维多峰值函数。 分别将 HS、IHS、ITHS、EHS 和 GHS 利用本文算 法思想进行改进,将其改进后分别称为 HS2 ,IHS2 , ITHS2 ,EHS2 和 GHS2 ,并将其与改进前的算法进行 比较。 检验改进后的算法是否比改进前的算法能够 获得更高精度的解,同时,检验其运行成本(运行时 间)是否降低。 3.1 实验环境和算法参数设置 本文实验采用戴尔工作站 T7500 Inter(R) Xe⁃ on(R) CPU E560@ 2.1 GHz, 8.0 GB 内存,Windows Server2003 Server 操作系统,所有测试程序采用 Mat⁃ lab R2009a 编写。 10 种算法参数设置如表 2。 表 1 6 个 Benchmark 函数( F1 ~ F6 ) Table 1 Six Benchmark functions 函数名称 Benchmark 函数表达式 搜索范围 参数值 F 1Ackley Function F1(x) = - 20e 1 5 1 D ∑ D i = 1 x 2 i - e 1 D ∑ D i = 1 cos(2πx i ) + 20 - e [ - 15,30] D x ∗ = (0,0,…,0) F1(x ∗ ) = 0 F 2 Griewank Function F2 = 1 4 000∑ D i = 1 x 2 i - ∏ D i = 1 (cos( xi i )) + 1 [ - 600,600] D x ∗ = (0,0,…,0) F2(x ∗ ) = 0 F 3Levy Function F3(x) = sin 2 (πy1 ) + ∑ D-1 i = 1 (yi - 1) 2 1 + 10 sin 2 (πyi [ ( + 1) ) ] + ( y D - 1)2 1 + 10 sin 2 (2πy ( D ) ) yi = 1 + (xi - 1) / 4,i = 1,2,…,D [ - 10,10] D x ∗ = (1,1,…,1) F3(x ∗ ) = 0 F 4Michalewics Function F4(x) = - ∑ D i = 1 sin(xi) sin(ixi 2 ( / π) ) 2m ;m = 10 [ - 10,π] D n = 5 F4(x ∗ ) = - 4.687 658 F 5Rastrigin Function F5(x) = 10D + ∑ D i = 1 xi 2 - 10cos(2πx ( i) ) [ - 5.12,5.12] D x ∗ = (0,0,…,0) F5(x ∗ ) = 0 F 6 Schwefel 2.26 Function F6(x) = 418.982 9D + ∑ D i = 1 x 2 i sin( xi ) [ - 512,512] D x ∗ = (420.968 7, 420.968 7,…,420.968 7) F6(x ∗ ) = 0 ·310· 智 能 系 统 学 报 第 10 卷

第2期 拓守恒,等:动态调整策略改进的和声搜索算法 .311. 表2参数设置 Table 2 Parameters setting 算法HMS HMCR PAR BW TP HS100.99 0.33 (xU-xL)/2000 HS2100.99 0.33 (xU-xL)/2000 TP=0.6,TP=5/D BWmax=(xU-xL)/20 IHS 10 0.99 PARmax=0.99,PARmin=0.1 1 BWmin=(xU-xL)/(le+8) BWmax=(xU-xL)/20 IHS, 100.99 PARmax=0.99.PARmin=0.1 TP=0.6.TPn=5/D BWmin=(xU-xL)/(1e+8) GHS 10 0.90 PARmax=0.99.PARmin=0.01 GHS, 100.90 PARmax=0.99,PARmin=0.01 / TP=0.6,TPn=5/D EHS 50 0.99 0.33 1 EHS,50 0.99 0.33 TP=0.6,TP=5/D THS100.99 PARmax=1,PARmin=0 THS2100.99 PARmax=1,PARmin=0 TPn=0.6,TP=5/D 表3在D=500时,5种和声算法及其利用本文算法改进的5种和声算法对6个测试函数的运行结果比较 Table 3 Results comparison between five HS algorithms and five improved HS algorithms F2 Fa 算法 Best Mean Std Runtime Best Mean Std Runtime Best Mean Std Runtime HS 2.34×10°2.50x1006.67×1022.52×1026.32×1016.75×1012.39x1023.06×1028.04×1029.70x1021.80×1021.61×103 HS21.39x1011.61×10-11.14×10-21.89×1024.20x10-15.31×1018.25×10-22.48×1021.09×10-41.24×1047.07E-061.53x103 GHs1.57×1031.64×1012.75×10-12.67×1021.88×1032.11×1031.49×1023.45×1027.11×1027.96×1024.40×109.03×102 GHS21.24×1024.29x1022.86×1022.42×1029.85×10-32.83×1012.72×1013.06×1021.30x1038.25x10-39.63×1038.86×102 Hs6.57×10-11.10x1001.74×10-13.79×1025.92×10-27.60x10-28.85×10-34.64x1025.27×10-21.05x10-14.09x10-21.24x103 IHS2 8.71×10-78.81×10-76.81×10-93.16×1022.69×10-13.70x10-41.65×10-34.00x1021.17×10121.19x10-22.75×10-49.71×102 THS7.90x1032.95×1021.18×10-23.17×1026.41×1031.92x10-19.97×10-23.87×1021.35×10°34.75×1032.16×10-31.70x103 THS21.50x10-33.49x10-.75×10-12.16×1026.66×10-167.72×10-165.67E-172.62x1021.50x10-321.50x10-20.00x10°1.62×103 EHS 4.55×1004.70x1008.66×10-25.02×1022.12×102.47×1011.58×1005.75×1021.11×1021.26×1027.58×10°2.04×103 EHS2 2.71×10~132.21×1056.85×1054.32×1027.77×10-61.26×1055.38×1055.17×1023.54E-151.25×1073.96×1071.24×103 F4 F6 算法 Best Mean Std Runtime Best Mean Std Runtime Best Mean Std Runtime HS -2.08×102-2.01×1024.92×1006.48×1021.10x1021.26×1021.07×1013.21×1024.57×1014.95×1012.42×10°2.98×102 HS2 -4.28×102-4.26×1022.03×1005.25×1021.13×1021.28×1028.39×1042.03×1026.99×1028.04×1026.73×1032.15×102 GHs-2.26×102-2.22×1022.90×1005.22×1021.61×1031.90×1031.19×1023.50x1023.35×1043.81×102.16x1033.47×102 GHS2-2.65x102-2.62×1021.55×1004.98x1028.81x10-41.10x10-11.69x10-13.14×1021.54×10-21.26x10°1.51×10°3.23x102 IHS -4.55x102-4.53×1022.43×1006.36×1021.02x1021.17×1025.45×10°4.99×1026.66×10°4.63×103.27×104.56×102 IHS2 -4.98×102-4.97×1021.33×10-15.83×1021.71×1021.20×10-11.05×1014.16×1021.37×1091.47×1096.97×10-113.83×102 THs-4.51×102-4.42×1023.69×1005.96×1024.35×10-35.94×10-25.25×10-24.38×1026.79×1021.39×1035.00×1025.66×102 THS2-4.98×102-4.98×1023.11×1014.89×1021.18×1014.27×1013.71×10112.97×1021.16×1091.39x1092.85×10103.98×102 EHS -1.63×102-1.58×1021.99×10°8.64×1024.43×1034.52×1034.70×106.68×1021.27×1031.32×1031.78×1036.48×102 EHS2-4.43×102-4.41×1021.38×10°8.10×1023.84×1024.52×1022.89x105.90×1022.36×1032.61×1031.33×1035.38×102 3.2实验结果与分析 次运行的最优目标函数适应值的平均值Mean,最优 为了保证算法测试的公平性,改进前的算法和值Bst,20次最优解的标准差(Std)和平均运行时 改进后的算法取相同的初始和声记忆库HM,每个算间(un time)。设置维数D=500,运行结果见表3。 法中随机数设置rand('twister',5489),每个算法程表中将HS、IHS、THS、EHs和GHS分别与HS2、 序独立运行20次,记录每次运行的过程,统计出20HS2、THS,、EHS2和GHS2进行比较,较好结果的用
表 2 参数设置 Table 2 Parameters setting 算法 HMS HMCR PAR BW TP HS 10 0.99 0.33 (xU-xL) / 2 000 / HS2 10 0.99 0.33 (xU-xL) / 2 000 TPmax = 0.6,TPmin = 5 / D IHS 10 0.99 PARmax = 0.99, PARmin = 0.1 BWmax = (xU-xL) / 20 BWmin = (xU-xL) / (1e+8) / IHS2 10 0.99 PARmax = 0.99, PARmin = 0.1 BWmax = (xU-xL) / 20 BWmin = (xU-xL) / (1e+8) TPmax = 0.6,TPmin = 5 / D GHS 10 0.90 PARmax = 0.99, PARmin = 0.01 / / GHS2 10 0.90 PARmax = 0.99, PARmin = 0.01 / TPmax = 0.6,TPmin = 5 / D EHS 50 0.99 0.33 / / EHS2 50 0.99 0.33 / TPmax = 0.6,TPmin = 5 / D ITHS 10 0.99 PARmax = 1, PARmin = 0 / / ITHS2 10 0.99 PARmax = 1, PARmin = 0 / TPmin = 0.6,TPmin = 5 / D 表 3 在 D = 500 时, 5 种和声算法及其利用本文算法改进的 5 种和声算法对 6 个测试函数的运行结果比较 Table 3 Results comparison between five HS algorithms and five improved HS algorithms 算法 F 1 Best Mean Std Runtime F 2 Best Mean Std Runtime F 3 Best Mean Std Runtime HS 2.34×10 0 2.50×10 0 6.67×10 -2 2.52×10 2 6.32×10 -1 6.75×10 -1 2.39×10 -2 3.06×10 2 8.04×10 -2 9.70×10 -2 1.80×10 -2 1.61×10 3 HS2 1.39×10 -1 1.61×10 -1 1.14×10 -2 1.89×10 2 4.20×10 -1 5.31×10 -1 8.25×10 -2 2.48×10 2 1.09×10 -4 1.24×10 -4 7.07E-06 1.53×10 3 GHS 1.57×10 1 1.64×10 1 2.75×10 -1 2.67×10 2 1.88×10 3 2.11×10 3 1.49×10 2 3.45×10 2 7.11×10 2 7.96×10 2 4.40×10 1 9.03×10 2 GHS2 1.24×10 -2 4.29×10 -2 2.86×10 -2 2.42×10 2 9.85×10 -3 2.83×10 -1 2.72×10 -1 3.06×10 2 1.30×10 -3 8.25×10 -3 9.63×10 -3 8.86×10 2 IHS 6.57×10 -1 1.10×10 0 1.74×10 -1 3.79×10 2 5.92×10 -2 7.60×10 -2 8.85×10 -3 4.64×10 2 5.27×10 -2 1.05×10 -1 4.09×10 -2 1.24×10 3 IHS2 8.71×10 -7 8.81×10 -7 6.81×10 -9 3.16×10 2 2.69×10 -11 3.70×10 -4 1.65×10 -3 4.00×10 2 1.17×10 -12 1.19×10 -12 2.75×10 -14 9.71×10 2 ITHS 7.90×10 -3 2.95×10 -2 1.18×10 -2 3.17×10 2 6.41×10 -3 1.92×10 -1 9.97×10 -2 3.87×10 2 1.35×10 -3 4.75×10 -3 2.16×10 -3 1.70×10 3 ITHS2 1.50×10 -13 3.49×10 -13 1.75×10 -13 2.16×10 2 6.66×10 -16 7.72×10 -16 5.67E-17 2.62×10 2 1.50×10 -32 1.50×10 -32 0.00×10 0 1.62×10 3 EHS 4.55×10 0 4.70×10 0 8.66×10 -2 5.02×10 2 2.12×10 1 2.47×10 1 1.58×10 0 5.75×10 2 1.11×10 2 1.26×10 2 7.58×10 0 2.04×10 3 EHS2 2.71×10 -13 2.21×10 -5 6.85×10 -5 4.32×10 2 7.77×10 -16 1.26×10 -5 5.38×10 -5 5.17×10 2 3.54E-15 1.25×10 -7 3.96×10 -7 1.24×10 3 算法 F 4 Best Mean Std Runtime F 5 Best Mean Std Runtime F 6 Best Mean Std Runtime HS -2.08×10 2 -2.01×10 2 4.92×10 0 6.48×10 2 1.10×10 2 1.26×10 2 1.07×10 1 3.21×10 2 4.57×10 1 4.95×10 1 2.42×10 0 2.98×10 2 HS2 -4.28×10 2 -4.26×10 2 2.03×10 0 5.25×10 2 1.13×10 -2 1.28×10 -2 8.39×10 -4 2.03×10 2 6.99×10 -2 8.04×10 -2 6.73×10 -3 2.15×10 2 GHS -2.26×10 2 -2.22×10 2 2.90×10 0 5.22×10 2 1.61×10 3 1.90×10 3 1.19×10 2 3.50×10 2 3.35×10 4 3.81×10 4 2.16×10 3 3.47×10 2 GHS2 -2.65×10 2 -2.62×10 2 1.55×10 0 4.98×10 2 8.81×10 -4 1.10×10 -1 1.69×10 -1 3.14×10 2 1.54×10 -2 1.26×10 0 1.51×10 0 3.23×10 2 IHS -4.55×10 2 -4.53×10 2 2.43×10 0 6.36×10 2 1.02×10 2 1.17×10 2 5.45×10 0 4.99×10 2 6.66×10 0 4.63×10 1 3.27×10 1 4.56×10 2 IHS2 -4.98×10 2 -4.97×10 2 1.33×10 -1 5.83×10 2 1.71×10 -2 1.20×10 -1 1.05×10 -1 4.16×10 2 1.37×10 -9 1.47×10 -9 6.97×10 -11 3.83×10 2 ITHS -4.51×10 2 -4.42×10 2 3.69×10 0 5.96×10 2 4.35×10 -3 5.94×10 -2 5.25×10 -2 4.38×10 2 6.79×10 2 1.39×10 3 5.00×10 2 5.66×10 2 ITHS2 -4.98×10 2 -4.98×10 2 3.11×10 -1 4.89×10 2 1.18×10 -11 4.27×10 -11 3.71×10 -11 2.97×10 2 1.16×10 -9 1.39×10 -9 2.85×10 -10 3.98×10 2 EHS -1.63×10 2 -1.58×10 2 1.99×10 0 8.64×10 2 4.43×10 3 4.52×10 3 4.70×10 1 6.68×10 2 1.27×10 5 1.32×10 5 1.78×10 3 6.48×10 2 EHS2 -4.43×10 2 -4.41×10 2 1.38×10 0 8.10×10 2 3.84×10 2 4.52×10 2 2.89×10 1 5.90×10 2 2.36×10 4 2.61×10 4 1.33×10 3 5.38×10 2 3.2 实验结果与分析 为了保证算法测试的公平性,改进前的算法和 改进后的算法取相同的初始和声记忆库 HM,每个算 法中随机数设置 rand(′twister′,5 489),每个算法程 序独立运行 20 次,记录每次运行的过程,统计出 20 次运行的最优目标函数适应值的平均值 Mean,最优 值 Best, 20 次最优解的标准差( Std)和平均运行时 间(run time)。 设置维数 D = 500,运行结果见表 3。 表中将 HS、 IHS、 ITHS、 EHS 和 GHS 分别与 HS2 、 IHS2 、ITHS2 、EHS2 和 GHS2 进行比较,较好结果的用 第 2 期 拓守恒,等:动态调整策略改进的和声搜索算法 ·311·