
1.2计算机中的数据 1.2.1数制与进位计数制 1.2.2二进制数的运算 1.2.3数制转换 1.2.4数据在计算机中的表示 本章首页
1.2 计算机中的数据 1.2.1 数制与进位计数制 1.2.2 二进制数的运算 1.2.3 数制转换 1.2.4 数据在计算机中的表示 本章首页

第章计扒然础积 1.2.1 数制与进位计数制 1,进位计激制的基李糯念 进位计数制:是指按进位的规则进行计数的方法。 进位计数制三要素: ① 数位:指数码在一个数中所处的位置,用士表示; ②基数:指在某种计数制中,每个数位上所能使用的数 码的个数,用R表示; ③位权:指在某种计数制中,每个数位上数码“1”所代 表的数值的大小。 本节首页
上一页 下一页 本节首页 1.2.1 数制与进位计数制 进位计数制: 是指按进位的规则进行计数的方法。 进位计数制三要素: ① 数位:指数码在一个数中所处的位置,用±n表示; ② 基数:指在某种计数制中,每个数位上所能使用的数 码的个数,用R表示; ③ 位权:指在某种计数制中,每个数位上数码“1”所代 表的数值的大小。 1.进位计数制的基本概念 本节首页

第章计扒然础积 1.2.1数制与进位计数制 2,进位计数制的基本特点 逢R进一 采用位权表示 例1:十进制数3058.72可表示为: (3058.72)10=3×103+0×102+5×101+8×100+7×101+2×10-2 例2:二进制数10111.01可表示为: (10111.01)2=1×24+0×23+1×22+1×21+1×20+0×2-1+1×2-2 例3:十六进制数3AB.65可表示为: (3AB.65)163×162+A×161+B×160+6×16-1+5×16-% 一页 本节首页
上一页 下一页 本节首页 2.进位计数制的基本特点 逢R进一 采用位权表示 例1:十进制数3058.72可表示为: (3058.72)10 = 3×103 + 0×102 + 5×101 + 8×100 + 7×10-1 + 2×10-2 例2:二进制数10111.01 可表示为: (10111.01)2 = 1×24 +0×23 +1×22 +1×21 +1×20 +0×2-1 +1×2-2 例3:十六进制数3AB.65可表示为: (3AB.65)16 = 3×162 + A×161 + B×160 + 6×16-1 + 5×16-2 1.2.1 数制与进位计数制 本节首页
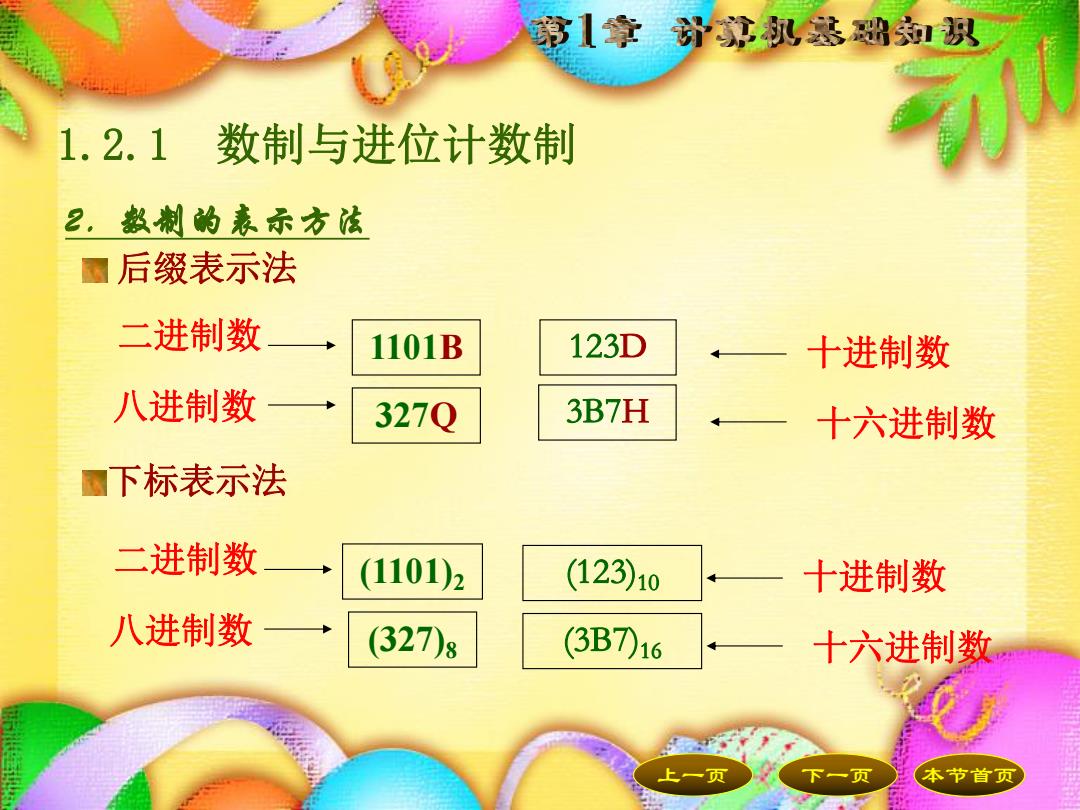
第1章计就认然础积 1.2.1数制与进位计数制 2,数制的表示方法 丽后缀表示法 二进制数 1101B 123D 十进制数 八进制数 327Q 3B7H 十六进制数 下标表示法 二进制数 (1101)2 (123)10 十进制数 八进制数 (327)8 (3B7)16 十六进制数 本节首页
上一页 下一页 本节首页 2.数制的表示方法 后缀表示法 下标表示法 1101B 八进制数 327Q 123D 十进制数 3B7H 十六进制数 二进制数 (1101)2 (327) 八进制数 8 (123)10 十进制数 (3B7)16 十六进制数 二进制数 1.2.1 数制与进位计数制 本节首页
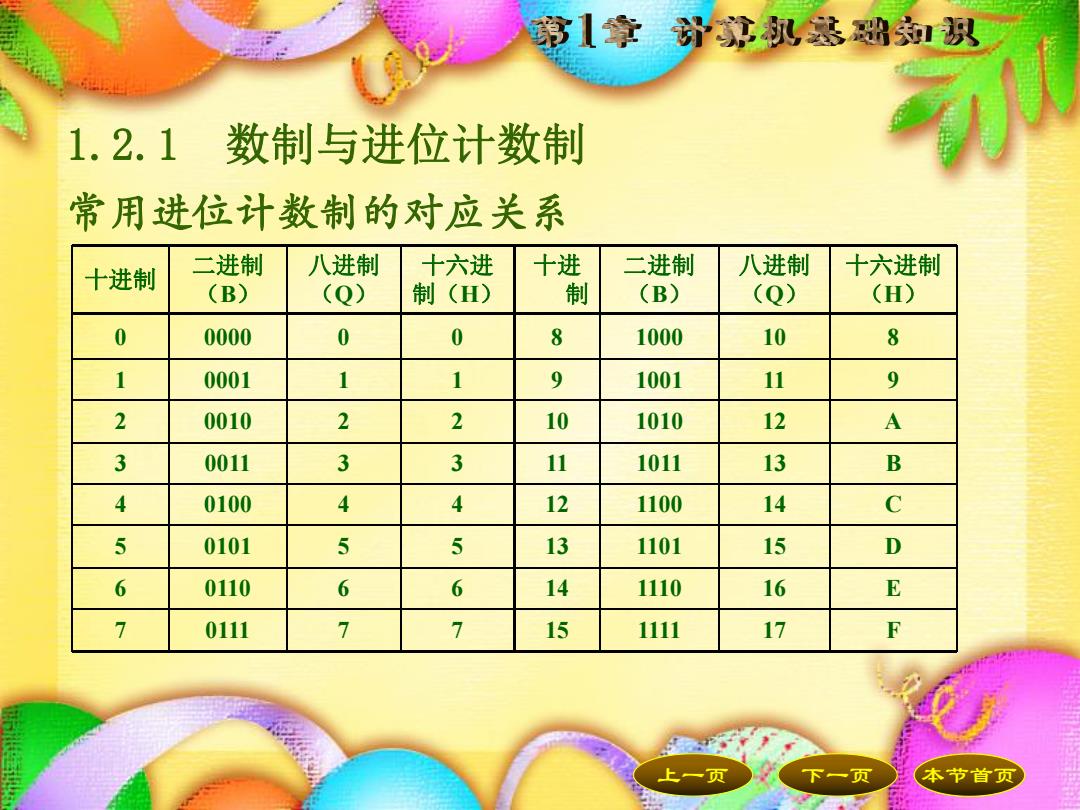
第1章计这扒然础积 1.2.1数制与进位计数制 常用进位计数制的对应关系 十进制 二进制 八进制 十六进 十进 二进制 八进制 十六进制 (B) (Q) 制(H) 制 (B) (Q) (H) 0 0000 0 0 8 1000 10 8 1 0001 1 1 9 1001 11 9 2 0010 2 2 10 1010 12 A 3 0011 3 3 11 1011 13 B 4 0100 4 4 12 1100 14 5 0101 5 5 13 1101 15 D 6 0110 6 6 14 1110 16 E 7 0111 7 7 15 1111 17 F 上一页 下一页 本节首页
上一页 下一页 本节首页 常用进位计数制的对应关系 十进制 二进制 (B) 八进制 (Q) 十六进 制(H) 十进 制 二进制 (B) 八进制 (Q) 十六进制 (H) 0 0000 0 0 8 1000 10 8 1 0001 1 1 9 1001 11 9 2 0010 2 2 10 1010 12 A 3 0011 3 3 11 1011 13 B 4 0100 4 4 12 1100 14 C 5 0101 5 5 13 1101 15 D 6 0110 6 6 14 1110 16 E 7 0111 7 7 15 1111 17 F 1.2.1 数制与进位计数制 本节首页