
Regular Definitions To write regular expression for some languages can be difficult,because their regular expressions can be quite complex.In those cases,we may use regular definitions. We can give names to regular expressions,and we can use these names as symbols to define other regular expressions. A regular definition is a sequence of the definitions of the form: d1→r1 where d;is a distinct name and d2→2 ri is a regular expression over symbols in U{d1,d2,…,d-1} dn→rn basic symbols previously defined names CS308 Compiler Theory 11
Regular Definitions • To write regular expression for some languages can be difficult, because thi l i b i l h h e ir regu lar express ions can be qu ite comp lex. In t hose cases, we may use regular definitions. • W i t l i d th We can g ive names to regu lar express ions, an d we can use these names as symbols to define other regular expressions. • A regular definition is a sequence of the definitions of the form: d1 → r1 where d where di is a distinct name and is a distinct name and d 2 → r 2 ri is a regular expression over symbols in . Σ∪{d d d } 1,d 2,..., di-1 } d n → rn 11 basic symbols previously defined names CS308 Compiler Theory

Regular Definitions (cont.) Ex:Identifiers in Pascal letter->A B ...Z al b...z digit-→0|1|.|9 id->letter (letter|digit ) If we try to write the regular expression representing identifiers without using regular definitions,that regular expression will be complex. (Al...Zlal..((Al..Zal..I(.))* Ex:Unsigned numbers in Pascal digit→011|.|9 digits→digit+ opt-fraction->(.digits ) opt-exponent>(E(+)?digits ) unsigned-num->digits opt-fraction opt-exponent CS308 Compiler Theory 2
Regular Definitions (cont.) • Ex: Identifiers in Pascal l tt e er → A|B| |Z| |b| | A | B | ... | Z | a | b | ... | z digit → 0 | 1 | ... | 9 id → letter (letter | digit ) * – If i h l i i id ifi i h i l d fi i i h If we try to write t he regular expression representing identifiers without using regular d efi nitions, t hat regular expression will be complex. (A|...|Z|a|...|z) ( (A|...|Z|a|...|z) | (0|...|9) ) * • Ex: Unsigned numbers in Pascal di git → 0 || | 1 ... | 9 digits → digit + opt-fraction → ( . digits ) ? o pt-ex ponent → ( (| E +|-) g) ? di gits ) ? unsigned-num → digits opt-fraction opt-exponent CS308 Compiler Theory 12
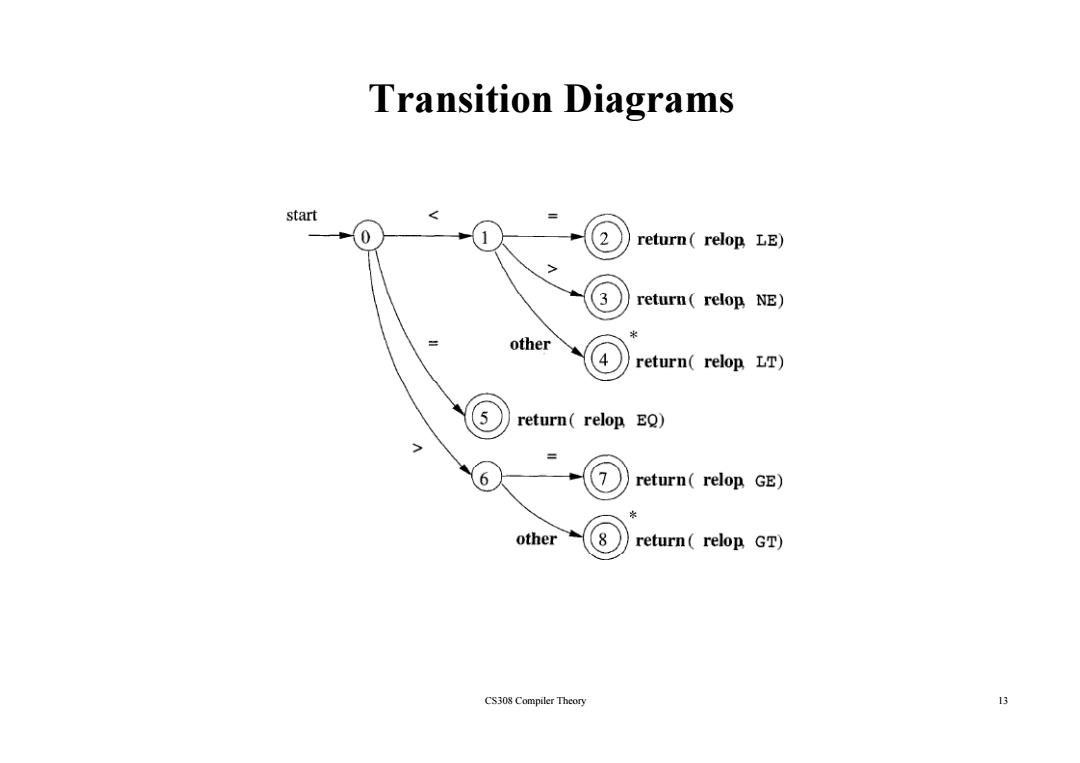
Transition Diagrams start 0 2 return(relop LE) > 3 return(relop NE) other return(relop LT) 5 return(relop EQ) 6 7 return(relop GE) other 8 return(relop GT) CS308 Compiler Theory 13
Transition Diagrams CS308 Compiler Theory 13

Transition-Diagram-Based Lexical Analyzer TOKEN getRelop() TOKEN retToken new (RELOP); while(1){/repeat character processing until a return or failure occurs * switch(state){ case 0:c nextChar(); if(c==’<’)state=1; e1seif(c=’=’)state=5; else if(c==’>’)state=6; else fail();/lexeme is not a relop * break; case1:··· case 8:retract(); retToken.attribute GT; return(retToken); CS308 Compiler Theory
Transition-Diagram-Based Lexical Analyzer CS308 Compiler Theory 14

The Lexical-Analyzer Generator Lex See Additional information about Lex (Lex.pdf) CS308 Compiler Theory
The Lexical-Analyzer Generator - Lex • See Additional information about Lex (Lex.pdf) CS308 Compiler Theory 15