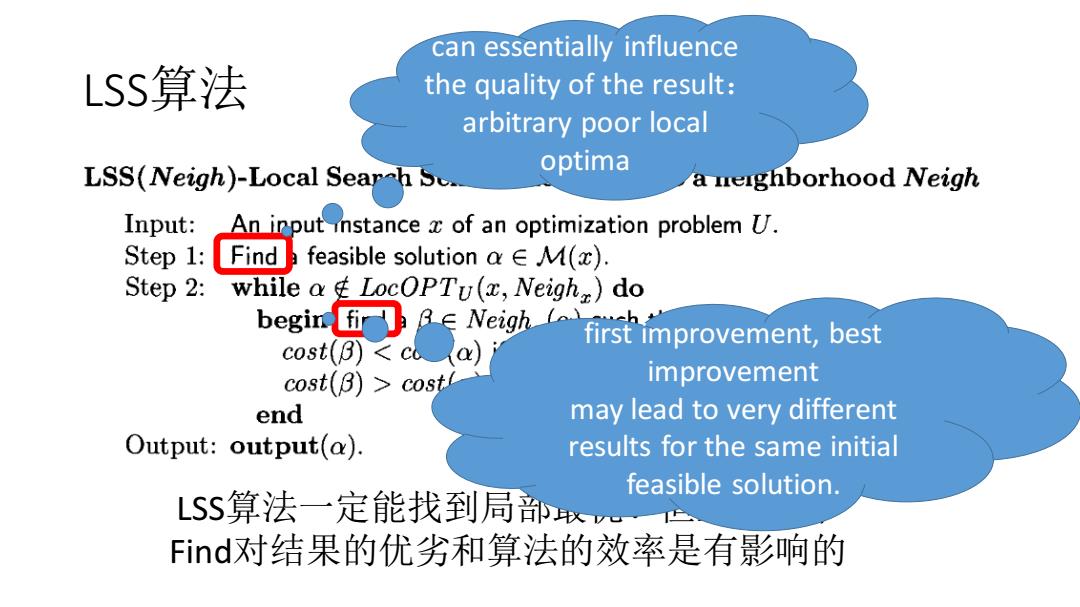
can essentially influence LSS算法 the quality of the result: arbitrary poor local LSS(Neigh)-Local Searh Sc. optima a neighborhood Neigh Input: An input instance z of an optimization problem U. Step 1:Finda feasible solution a E M(x) Step 2:while ag LocOPTu(x,Neigh)do begin fir∈Neigh cost(B)<cla)i first improvement,best cost(B)>cost improvement end may lead to very different Output:output(a). results for the same initial feasible solution. LSS算法一定能找到局w Find对结果的优劣和算法的效率是有影响的
LSS算法 LSS算法一定能找到局部最优!但上述两个 Find对结果的优劣和算法的效率是有影响的 can essentially influence the quality of the result: arbitrary poor local optima first improvement, best improvement may lead to very different results for the same initial feasible solution

必须解决局部搜索方法中的 poor local optima”问题 The basic idea of simulated annealing is to add the possibility of leaving a local optimum (i.e.,to move to a weaker solution than the current one)by some kind of coin tossing (random decision)
必须解决局部搜索方法中的 “poor local optima”问题

物理学中的“退火”是什么? (1)The temperature of the heat bath is increased to a maximum value at which the solid melts.This causes all the particles to arrange themselves randomly. (2)The temperature of the heat bath is slowly decreased according to a given cooling schedule until a low-energy state of the solid (a perfect crystal structure)is achieved
物理学中的“退火”是什么?

Metropolis:算法:对退火过程的模拟 Step 1:Let s be the initial state of the solid with energy E(s)and let T be the initial temperature of the heat bath. Step 2: Generate a state g from s by applying a perturbation mechanism, which transfers s into g by a small random distortion (for instance, by a random displacement of a small particle). if E(a)<E(s)then s:=a else accept g as a new state with the probability 模拟退火算法对LSS E(Q-E( 算法的最大改进 p(s→g)=e (i.e,remain in state s with the probability 1-p(sg)). Step 3:Decrease T appropriately. if T is not too close to 0 repeat Step 2, else output(s)
Metropolis算法:对退火过程的模拟 模拟退火算法对LSS 算法的最大改进