
3.1栈 栈的特点 后进先出(LFO) 3.1.1抽象数据类型栈的定义 入栈 出栈 栈顶:对栈进行操作的一端。 栈顶指针:指示栈顶位置的指针。 栈顶 栈的长度:栈中元素的个数。 假设栈S=(a1,a2,a3,an). 3n-1 则a称为栈底元素,an为栈顶元 素。插入的过程称为入栈,删除 82 的过程称为出栈。 栈底 a 栈称为后进先出表 (LIFO)。 栈的示意图,父 -6
— 6— 3.1 栈 栈顶:对栈进行操作的一端。 栈顶指针:指示栈顶位置的指针。 栈的长度:栈中元素的个数。 假设栈S=(a1, a2, a3, …,, an), 则a1称为栈底元素,an为栈顶元 素。插入的过程称为入栈,删除 的过程称为出栈。 栈称为后进先出表(LIFO)。 an an-1 … a2 a1 入栈 出栈 栈顶 栈底 栈的示意图 栈的特点 后进先出(LIFO) 3.1.1 抽象数据类型栈的定义
3.1栈 栈的特点 后进先出 3.1.1抽象数据类型栈的定义 (LIFO) 栈的示意图 出栈 进栈 第一个进栈的元素在栈底; 栈顶 最后一个进栈的元素在栈顶; Ap an-1 第一个出栈的元素为栈顶元素; 最后一个出栈的元素为栈底元素。 a, 栈底 1945
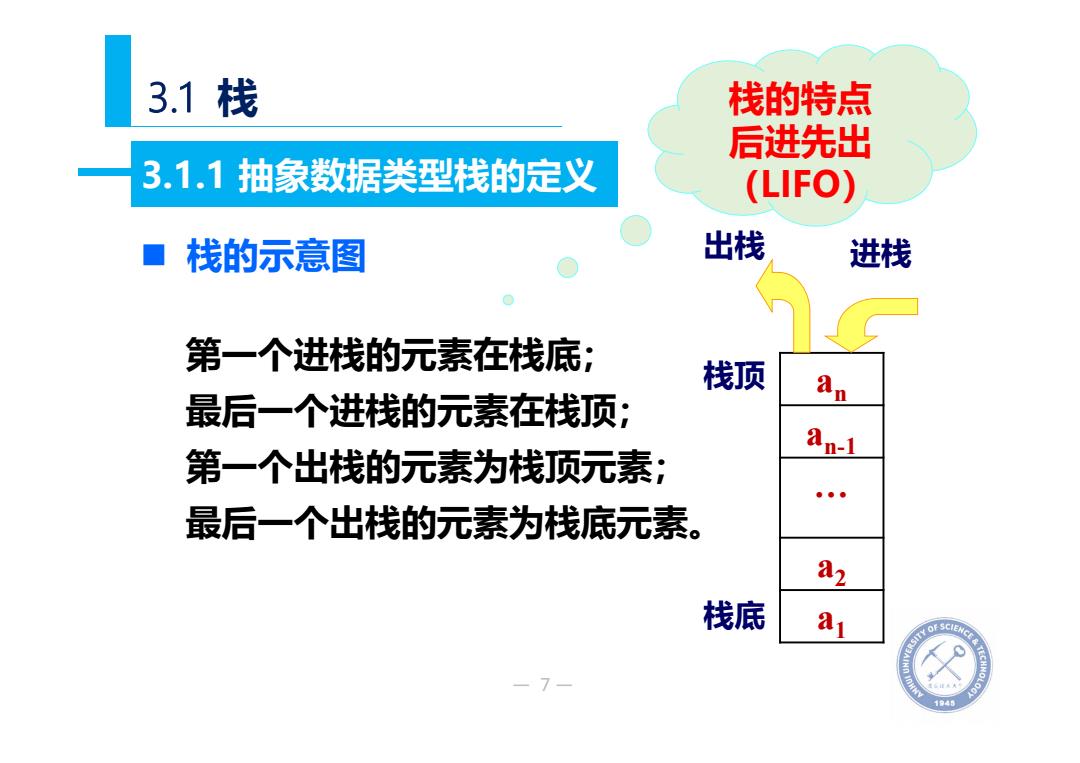
— 7— 3.1 栈 栈的示意图 an an-1 … a2 a1 栈顶 栈底 出栈 进栈 第一个进栈的元素在栈底; 最后一个进栈的元素在栈顶; 第一个出栈的元素为栈顶元素; 最后一个出栈的元素为栈底元素。 栈的特点 后进先出 3.1.1 抽象数据类型栈的定义 (LIFO)

前课回顾 SqList L 定位 ListInsert Sq(&L,i,e) 移动 elem 顺序表 插入表长 length listsize 定位 ListDelete Sq(&L,i,&e) 赋值 移动/表长 定位 LNode ListInsert L(L,i,e) 分配结点 链表 data next 插入 LinkList L 定位 ListDelete L(L,i,&e) 删除 释放结点刀 -8
— 8— — 8— 前课回顾 顺序表 链表 SqList L elem length listsize data next LNode LinkList L ListInsert_L(L, i, e) ListInsert_Sq(&L, i, e) 定位 移动 插入/表长 ListDelete_Sq(&L, i, &e) 定位 赋值 移动/表长 定位 分配结点 插入 ListDelete_L(L, i, &e) 定位 删除 释放结点

3.1栈 3.1.1抽象数据类型栈的定义 ADT Stack 数据对象: D={a;a,∈ElemSet,i=1,2,,n,n≥0} 数据关系: R1={<a-1wa;>|a-1wa;∈D,i=2,,n} 约定an端为栈顶,a1端为栈底。 基本操作: ADT Stack -9 1945
— 9— 3.1 栈 ADT Stack { 数据对象: D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 } 数据关系: R1={ <ai-1, ai >| ai-1, ai∈D, i=2,...,n } 约定an 端为栈顶,a1 端为栈底。 基本操作: } ADT Stack 3.1.1 抽象数据类型栈的定义

3.1栈 一3.1.1抽象数据类型栈的定义 ■栈的基本操作 DestroyStack(&S) InitStack(&S) StackEmpty(S) GetTop(S,&e) ClearStack(&S) Push(&S,e) Pop(&S,&e) -10 1945
— 10 — 3.1 栈 InitStack(&S) ClearStack(&S) StackEmpty(S) GetTop(S, &e) Push(&S, e) Pop(&S, &e) 栈的基本操作 DestroyStack(&S) 3.1.1 抽象数据类型栈的定义