
K-L变换原理 口基于Karhunen-Loeve?变换的特征提取方法是针对在 特征空间分布的样本特征向量和类别信息,结合样本 类别信息实行空间变换,找到可近似表示原样本的维 数较少的组合特征,达到降维的目的 ☐不失一般性,认为D为无限大的情况,并设原信号x可 用一组正交变换基u表示: ,= 1 i=j 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 K-L变换原理 □基于Karhunen-Loeve变换的特征提取方法是 □不失一般性,认为D为无限大的情况,并设原信号x可 用一组正交变换基uj表示:

K-L变换原理 5 ☐现要求降维至d维,也就是说将d+1维以上的成分略去,其 表示成: 显然原信号会因此受到一些损失,而每个信号的 损失则表示成x与x之差。 “% -=∑c +] 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 □现要求降维至d 维,也就是说将d+1维以上的成分略去,其 表示成: ■ 显然原信号会因此受到一些损失,而每个信号的 损失则表示成x与 之差。 K-L变换原理

K-L变换原理 ☐现在的问题是如何在给定一个训练样本集条件下要找一 个好的正交变换,能使这种误差从总体上来说是最小 口在这种情况下最常用的指标是均方误差最小,或称均方 误差的期望值最小,即: 5=E[(-y(-刘 ■或者说要找一个正交变换,使样本集截取所造成的 损失的均方误差的期望值为最小。 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 □现在的问题是如何在给定一个训练样本集条件下要找一 个好的正交变换,能使这种误差从总体上来说是最小 □在这种情况下最常用的指标是均方误差最小,或称均方 误差的期望值最小,即: ■ 或者说要找一个正交变换,使样本集截取所造成的 损失的均方误差的期望值为最小。 K-L变换原理
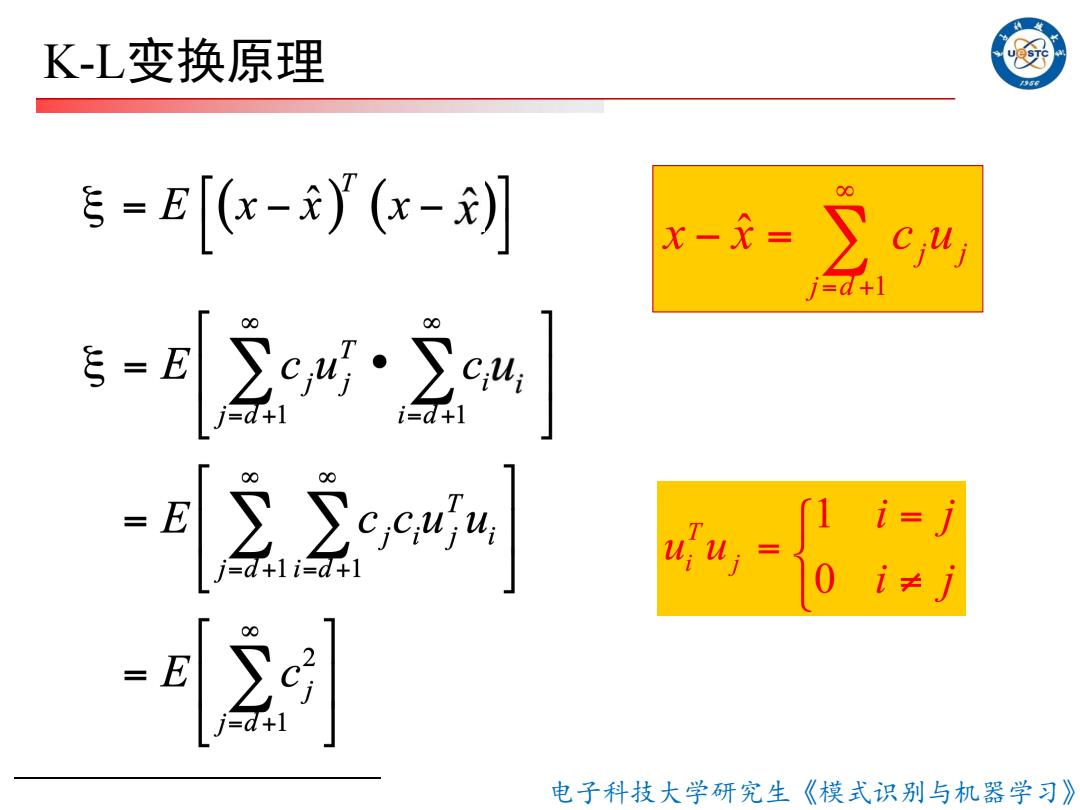
K-L变换原理 E=[-y(-刿 x-龙= ∑c4 i=d+ -84gar d+1 -22ee网 -6 -E 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 K-L变换原理

K-L变换原理 956 -6 公%,→4=%公” ,=4x c=x, 区[g小2i 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 K-L变换原理