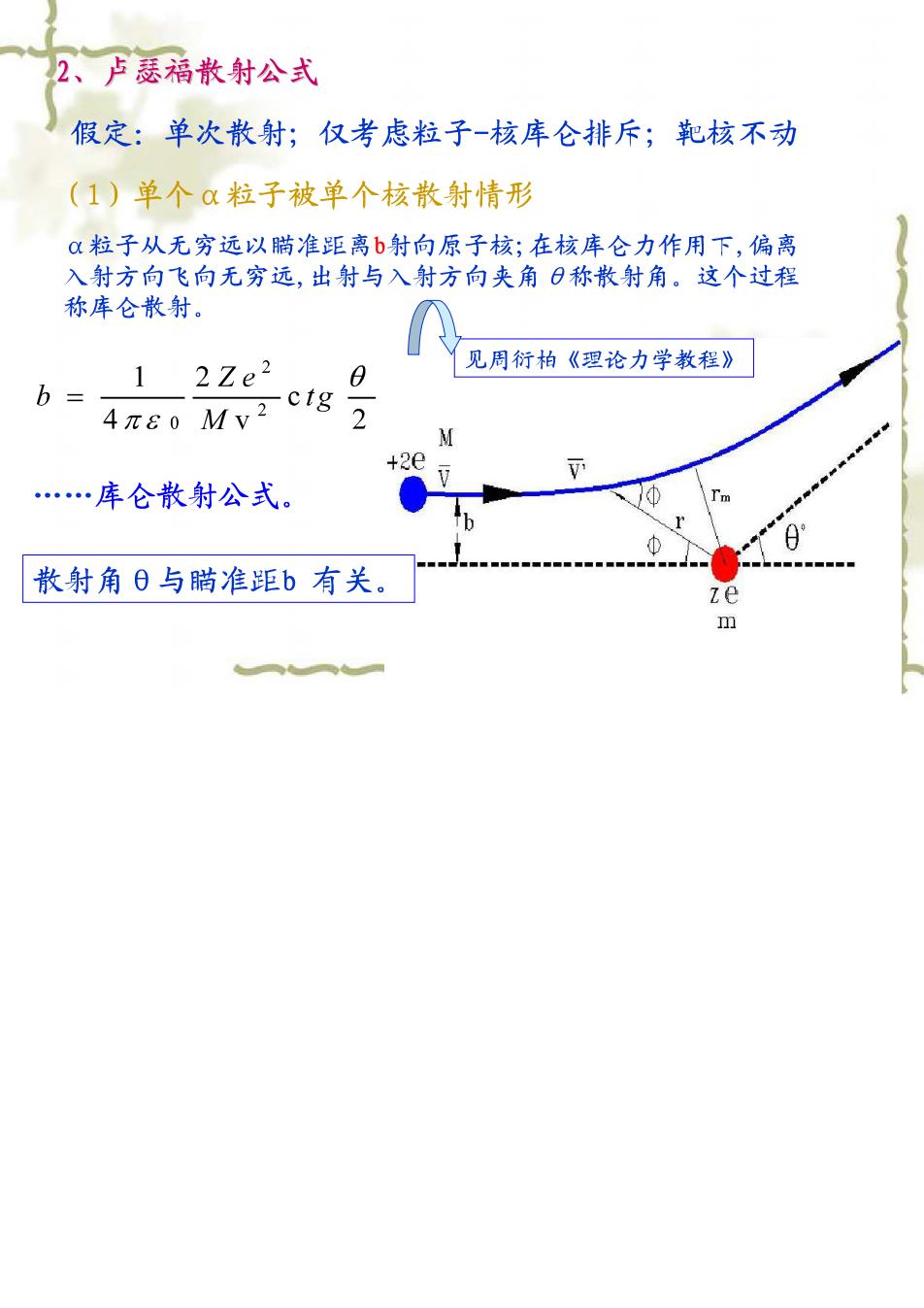
2、卢瑟福散射公式 假定:单次散射;仅考虑粒子-核库仑排斥;靶核不动 (1)单个Q粒子被单个核散射情形 α粒子从无穷远以瞒准距离b射向原子核;在核库仑力作用下,偏离 入射方向飞向无穷远,出射与入射方向夹角日称散射角。这个过程 称库仑散射。 见周衍柏《理论力学教程》 1 2Ze2 b= 4πe0Mv2ctg 2 +2e 1 .库仑散射公式。 散射角日与瞄准距b有关。 m

问题:b不能直接测量,实验可测散射到日-日+d0的粒子数。 0←bB+d0←b+db db +d d o 那些瞄准距在b-b+db间,或者说, 凡通过dg环形面积的a粒子,散射 后必定射向日-日+d日对应的空心锥 壳。粒子射到0-0+d0角度的 几率正比于环形面积。 do=2bdb=π( 4πEo

d2=2πsin0d0=4πsin号cos号d0 Ze2 do=(- 1-)2( 4π80 )2、Q sing .卢瑟福散射公式 dσ:称为原子核的有效散射截面。具有面积量纲。 (2)a粒子被靶散射到0.0+d0的总截面 设N为靶的单位体积原子数,靶厚t,靶被打中的面积A。假 设靶原子对射来的α粒子前后互不遮蔽(对薄的金属箔成 立)。则与一给定立体角d2相应的总散射截面: d∑=NtA*do

3)n个a粒子中被靶散射到0.0+d0的粒子数dn n→Adn→E =2=ndo→do=dh nNt do:代表了一个a粒子被一个核散射到0-0+d0之间那么 一个立体角dD内的几率,故有效散射截面也称做几 率。dσ的物理意义. dn in1 -nNi( Ze2 dΩ 4π80 M)

3、卢瑟福散射公式的实验验证 dn sin nNt( 12Ze do 2 4πe0 dn' dn dg"-a 1)同一a粒子源,同一个靶 dn' do' 5m+9=常数 2)同一粒子源,同一种材料的靶,同 x 3)同一个靶,同一个散射角 dn' v4=常数 d2' 4)用同一个粒子源,在同一个散射角,对同一Nt值 dn oc Z2 dΩ