
Generating Equivalent Expressions Database System Concepts-7th Edition 16.7 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 16.7 ©Silberschatz, Korth and Sudarshan th Edition Generating Equivalent Expressions

Transformation of Relational Expressions Two relational algebra expressions are said to be equivalent if the two expressions generate the same set of tuples on every lega/database instance Note:order of tuples is irrelevant we don't care if they generate different results on databases that violate integrity constraints In SQL,inputs and outputs are multisets of tuples Two expressions in the multiset version of the relational algebra are said to be equivalent if the two expressions generate the same multiset of tuples on every legal database instance. An equivalence rule says that expressions of two forms are equivalent Can replace expression of first form by second,or vice versa Database System Concepts-7th Edition 16.8 ©Silberscha乜,Korth and Sudarshan
Database System Concepts - 7 16.8 ©Silberschatz, Korth and Sudarshan th Edition Transformation of Relational Expressions ▪ Two relational algebra expressions are said to be equivalent if the two expressions generate the same set of tuples on every legal database instance • Note: order of tuples is irrelevant • we don’t care if they generate different results on databases that violate integrity constraints ▪ In SQL, inputs and outputs are multisets of tuples • Two expressions in the multiset version of the relational algebra are said to be equivalent if the two expressions generate the same multiset of tuples on every legal database instance. ▪ An equivalence rule says that expressions of two forms are equivalent • Can replace expression of first form by second, or vice versa

Equivalence Rules 1.Conjunctive selection operations can be deconstructed into a sequence of individual selections. 01A2(E)三001(C2(E)》 2.Selection operations are commutative. 0,(C92(E)》三O2(C,(E) 3.Only the last in a sequence of projection operations is needed,the others can be omitted. Π(2((ΠLn(E)…)》三ΠL,(E) here L1∈L2.∈Ln 4.Selections can be combined with Cartesian products and theta joins. a.09(E1XE2)≡E1☒9E2 b.091(E1凶02E2)三E1☒91A2E2 Database System Concepts-7th Edition 16.9 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 16.9 ©Silberschatz, Korth and Sudarshan th Edition Equivalence Rules 1. Conjunctive selection operations can be deconstructed into a sequence of individual selections. σ1 2 (E) ≡ σ1 (σ2 (E)) 2. Selection operations are commutative. σ1 (σ2 (E)) ≡ σ2 (σ1 (E)) 3. Only the last in a sequence of projection operations is needed, the others can be omitted. L1 ( L2 (…( Ln (E))…)) ≡ L1 (E) where L1 ⊆ L2 … ⊆ Ln 4. Selections can be combined with Cartesian products and theta joins. a. σ (E1 x E2 ) ≡ E1 ⨝ E2 b. σ 1 (E1 ⨝2 E2 ) ≡ E1 ⨝ 1∧2 E2

Equivalence Rules (Cont.) 5.Theta-join operations (and natural joins)are commutative. E1☆E2≡E2☒E1 6.(a)Natural join operations are associative: (E1☒E2)☒E3≡E1凶(E2☒E3) (b)Theta joins are associative in the following manner: (E1凶01E2)凶2A3E3三E1凶91A03(E2凶2E3) where 02 involves attributes from only E2 and E3. Database System Concepts-7th Edition 16.10 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 16.10 ©Silberschatz, Korth and Sudarshan th Edition Equivalence Rules (Cont.) 5. Theta-join operations (and natural joins) are commutative. E1 ⨝ E2 ≡ E2 ⨝ E1 6. (a) Natural join operations are associative: (E1 ⨝ E2 ) ⨝ E3 ≡ E1 ⨝ (E2 ⨝ E3 ) (b) Theta joins are associative in the following manner: (E1 ⨝ 1 E2 ) ⨝ 2 3 E3 ≡ E1 ⨝1 3 (E2 ⨝ 2 E3 ) where 2 involves attributes from only E2 and E3
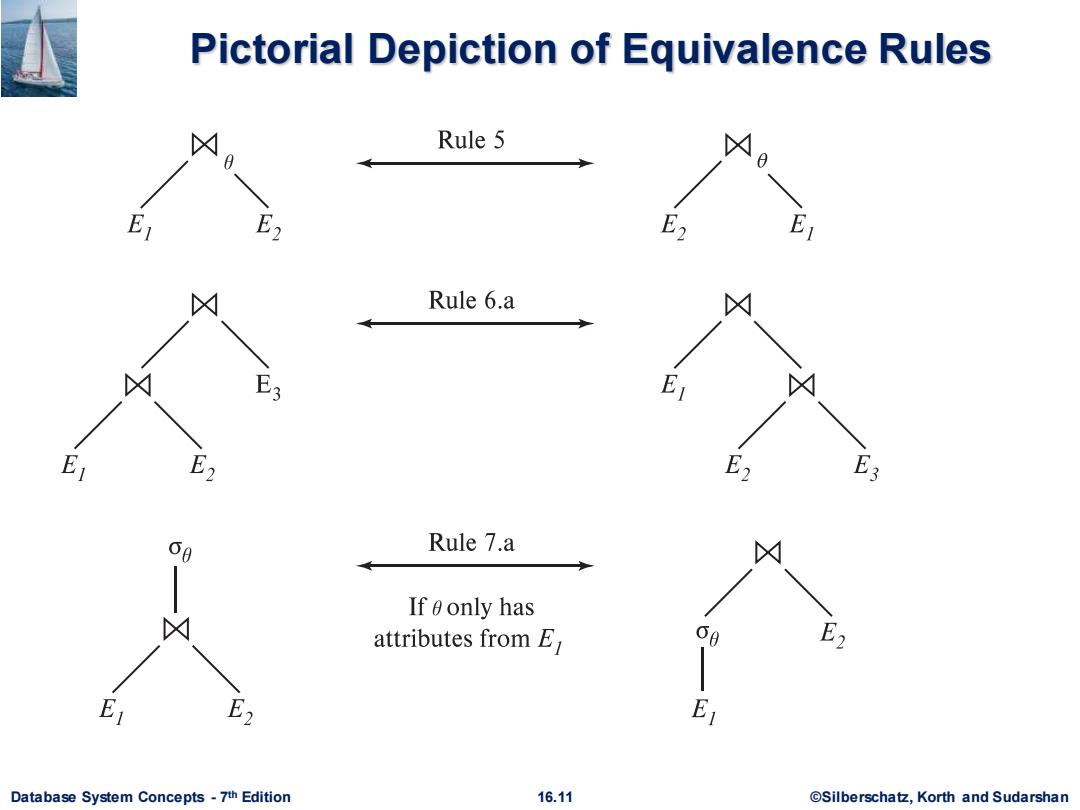
Pictorial Depiction of Equivalence Rules Rule 5 E1 E2 E2 Rule 6.a ◇外 Er E E2 E2 E3 60 Rule 7.a 凶 If 0 only has attributes from E 60 E2 Er E2 Database System Concepts-7th Edition 16.11 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 16.11 ©Silberschatz, Korth and Sudarshan th Edition Pictorial Depiction of Equivalence Rules