
生成树、生成森林 连通图G的生成树,是G的包含其全部n个顶点的 个极小连通子图。它必定包含且仅包含G的n-1条边。 极小连通子图意思是:该子图是G的连通子图,在该 子图中删除任何一条边,子图不再连通 非连通图的生成树则组成一个生成森林。若图中有 个顶点,m个连通分量,! 则生成森林中有n-m条边。 V3 连通图G1 G1的生成树
◼ 生成树、生成森林 V0 V3 V4 V1 V2 V0 V3 V4 V1 V2 V0 V4 V3 V1 V2 连通图 G1 G1的生成树 连通图G的生成树,是G的包含其全部n个顶点的一 个极小连通子图。它必定包含且仅包含G的n-1条边。 极小连通子图意思是:该子图是G 的连通子图,在该 子图中删除任何一条边,子图不再连通。 非连通图的生成树则组成一个生成森林。若图中有n 个顶点,m个连通分量,则生成森林中有n-m条边

■例: 2 5 路径:1,2,3,5,6,3 路径长度:5 简单路径:1,2,3,5 3 回路:1,2,3,5,6,3,1 简单回路:3,5,6,3 G1 路径:1,2,5,7,6,5,2,3 5 路径长度:7 简单路径:1,2,5,7,6 3 回路:1,2,5,7,6,5,2,1 简单回路:1,2,3,1 G2
G2 G1 2 4 5 1 3 6 1 7 3 2 4 6 5 路径:1,2,3,5,6,3 路径长度:5 简单路径:1,2,3,5 回路:1,2,3,5,6,3,1 简单回路:3,5,6,3 路径:1,2,5,7,6,5,2,3 路径长度:7 简单路径:1,2,5,7,6 回路:1,2,5,7,6,5,2,1 简单回路:1,2,3,1 ◼ 例:

7.2图的存储表示 图是一种结构复杂的数据结构, 表现在不仅各个顶 点的度可以千差万别,而且顶点之间的逻辑关系也错 综复杂。从图的定义可知,一个图的信息包括两部分, 即图中顶点的信息以及描述顶点之间的关系(边或者 弧)的信息。 因此无论采用什么方法建立图的存储结 构,都要完整、准确地反映这两方面的信息。 图通常有邻接矩阵、邻接表、 邻接多重表和十字链 表等表示方法
图是一种结构复杂的数据结构,表现在不仅各个顶 点的度可以千差万别,而且顶点之间的逻辑关系也错 综复杂。从图的定义可知,一个图的信息包括两部分, 即图中顶点的信息以及描述顶点之间的关系(边或者 弧)的信息。因此无论采用什么方法建立图的存储结 构,都要完整、准确地反映这两方面的信息。 图通常有邻接矩阵、邻接表、邻接多重表和十字链 表等表示方法。 7.2 图的存储表示

72.1邻接矩阵 定义:在邻接矩阵表示中,除了用一维数组存放 顶点本身信息外,还用一个矩阵表示各个顶点之间 的邻接关系。这个矩阵称为邻接矩阵。 假设图G=(V,E)有个确定的顶点,即V= {YoV1,Vn-1},则表示G中各顶点相邻关系为一 个n×n的矩阵,矩阵的元素为: 若(V,Y或<v,Y>是E(G)中的边 1 A[= 0若(N,)或<VY,>不是E(©)中的边
7.2.1 邻接矩阵 定义:在邻接矩阵表示中,除了用一维数组存放 顶点本身信息外,还用一个矩阵表示各个顶点之间 的邻接关系。这个矩阵称为邻接矩阵。 假设图G=(V, E)有n个确定的顶点,即V= {v0 ,v1 ,…, vn-1 } ,则表示G中各顶点相邻关系为一 个n×n的矩阵,矩阵的元素为 : A[i][j]= 1 若(vi ,vj )或<vi ,vj>是E(G)中的边 0 若(vi ,vj )或<vi ,vj>不是E(G)中的边
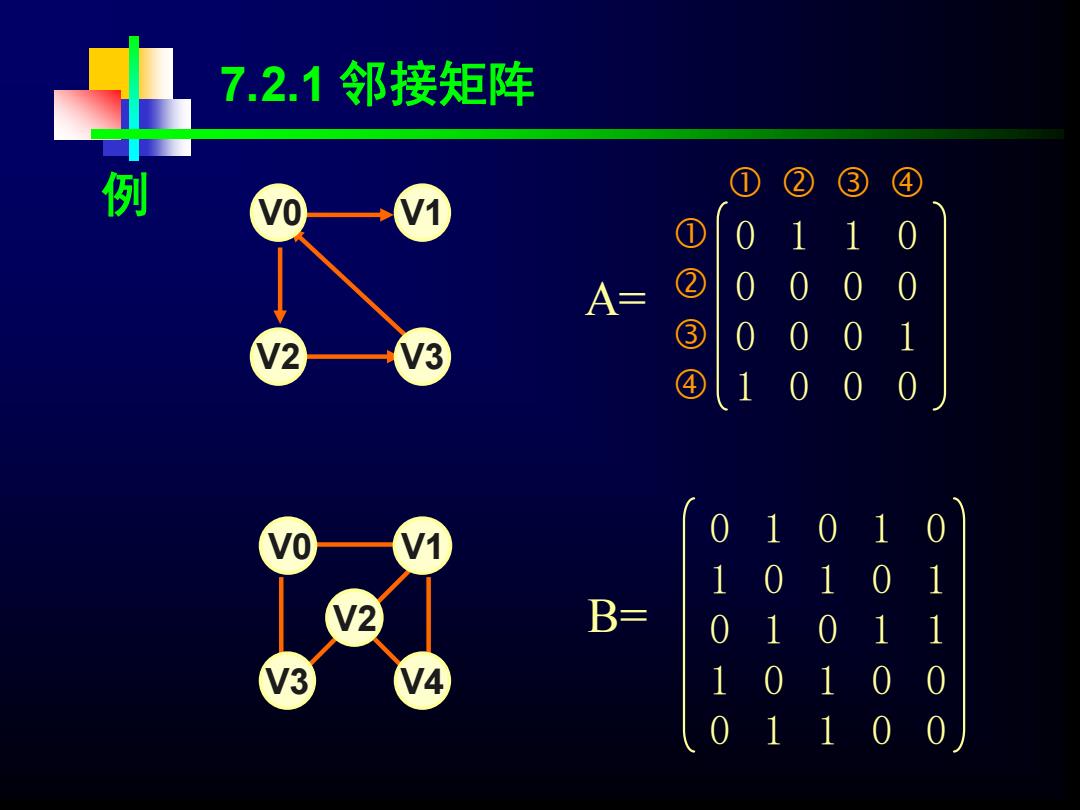
7.2.1邻接矩阵 例 ① ② ④ Vo I1 ① A= ② ③ /3 ④ 1 1 B 3 4 1 0
V0 V1 V2 V3 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 A= 例 V0 V3 V4 V1 V2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 B= 7.2.1 邻接矩阵