
二进制与八、十六进制数的转换 辣凤利学拉未学丽 示例: 100110110111.010100 ↓↓↓↓↓↓ (4 6 6 7。 24)8 000110110111.0100 ↓↓ ↓ (1 B 7.4)16
二进制与八、十六进制数的转换 0001 1011 0111.0100 示例: 100 110 110 111 . 010 100 ( 4 6 6 7 . 2 4 )8 ( 1 B 7 . 4 )16

数制的转换 0 计草机利学与校术学网 ■例如将3A6.C5H转换成二进制数。 3A6 .C 5 ↓↓↓↓ 001110100110.11000101 转换结果为3A6.C5H=1110100110.11000101B。 其他进制之间的转换可以通过二进制作为中间桥梁 ,先转化为二进制数,再转化为其他进制数
数制的转换 ◼ 例如 将3A6.C5H转换成二进制数。 3 A 6 . C 5 ↓ ↓ ↓ ↓ ↓ 0011 1010 0110 . 1100 0101 转换结果为3A6.C5H = 1110100110.11000101B。 其他进制之间的转换可以通过二进制作为中间桥梁 ,先转化为二进制数,再转化为其他进制数
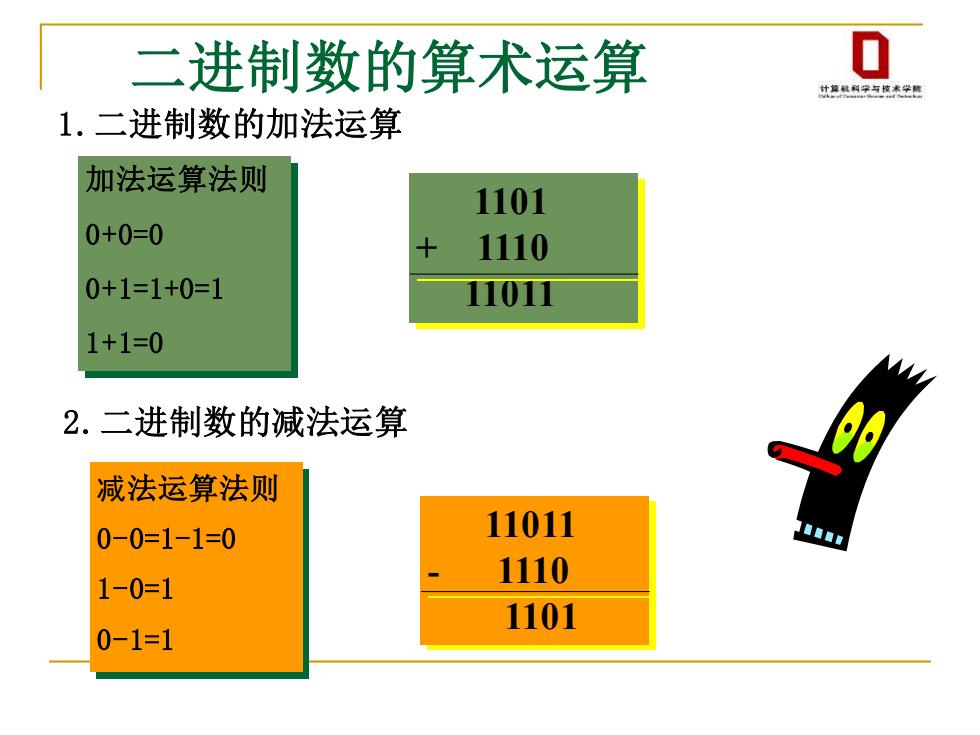
二进制数的算术运算 0 什草凤利学与拉未学魔 1.二进制数的加法运算 加法运算法则 1101 0+0=0 1110 0+1=1+0=1 1101I 1+1=0 2.二进制数的减法运算 减法运算法则 0-0=1-1=0 11011 1-0=1 1110 1101 0-1=1
二进制数的算术运算 1.二进制数的加法运算 2.二进制数的减法运算 加法运算法则 0+0=0 0+1=1+0=1 1+1=0 1101 + 1110 11011 减法运算法则 0-0=1-1=0 1-0=1 0-1=1 11011 - 1110 1101
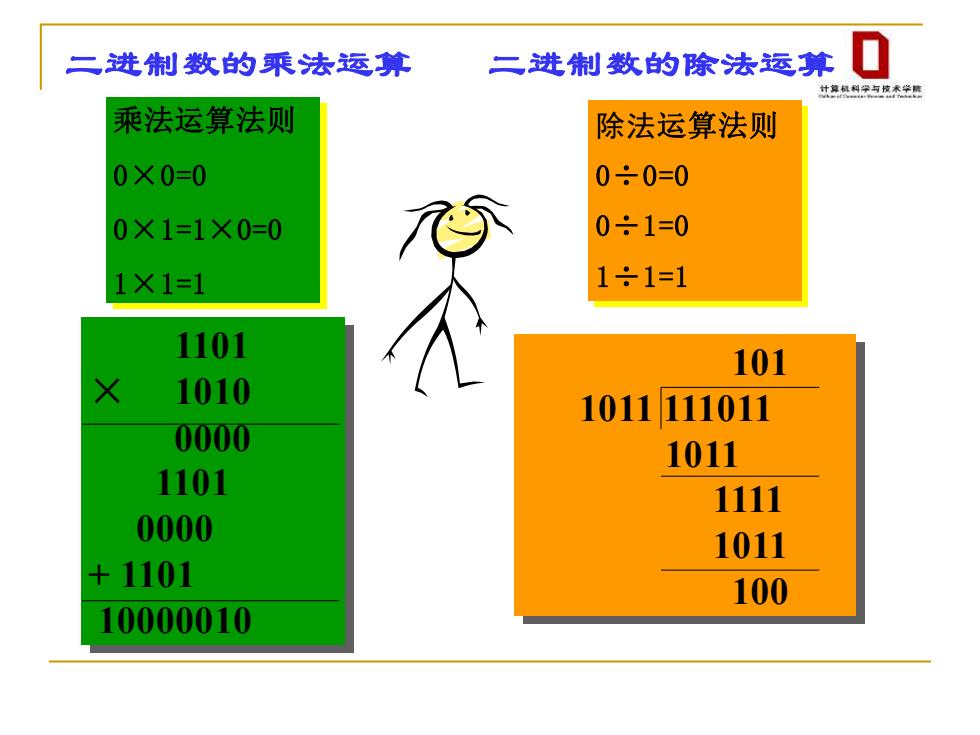
二进制数的乘法运算 二进制数的除法运算 0 计草机利学与愤术学码 乘法运算法则 除法运算法则 0×0=0 0÷0=0 0×1=1×0=0 0÷1=0 1×1=1 1÷1=1 1101 101 1010 1011111011 0000 1011 1101 1111 0000 1011 +1101 100 10000010
二进制数的乘法运算 二进制数的除法运算 乘法运算法则 0×0=0 0×1=1×0=0 1×1=1 除法运算法则 0÷0=0 0÷1=0 1÷1=1 1101 × 1010 0000 1101 0000 + 1101 10000010 101 1011 111011 1011 1111 1011 100
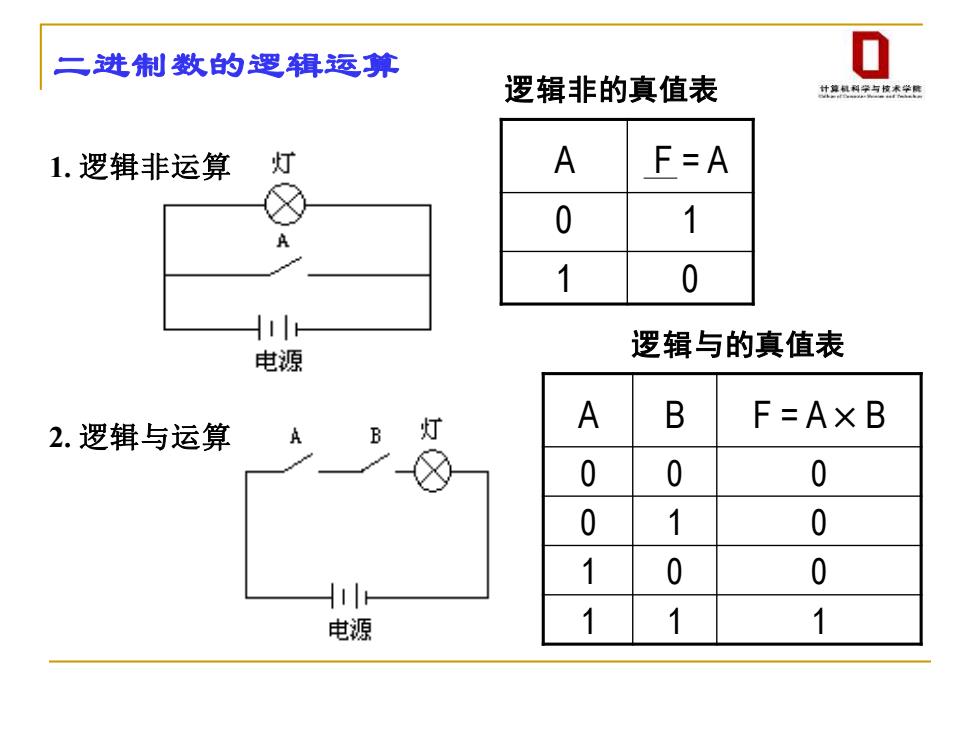
二进制数的逻辑运算 0 逻辑非的真值表 什草凤利学与拉未学魔 1.逻辑非运算 灯 A F=A 0 1 1 0 电源 逻辑与的真值表 灯 A B F=AxB 2.逻辑与运算 B 0 0 0 0 1 0 1 0 0 H 电源 1 1 1
二进制数的逻辑运算 1. 逻辑非运算 逻辑非的真值表 A F = A 0 1 1 0 2. 逻辑与运算 逻辑与的真值表 A B F = A×B 0 0 0 0 1 0 1 0 0 1 1 1