
1.数制及其转换 0 件菜凤利学与拉未学腐 口常用数制 口数制的转换 口二进制的运算规则
1.数制及其转换 ❑ 常用数制 ❑ 数制的转换 ❑ 二进制的运算规则

数制及其转换 数制的概念 数制(Numbering system)即表示数值的方法,有 非进位数制和进位数制两种。 ■表示数值的数码与它在数中的位置无关的数制称为 非进位数制。 ■按进位的原则进行计数的数制称为进位数制,简称 “进制
数制及其转换 数制的概念 数制(Numbering system)即表示数值的方法,有 非进位数制和进位数制两种。 ◼ 表示数值的数码与它在数中的位置无关的数制称为 非进位数制。 ◼ 按进位的原则进行计数的数制称为进位数制,简称 “进制”

几个名词术语 什草凤利学与拉未学脑 ·数码:一组用来表示某种数制的符号。如:1、2、3、 4、A、B、C等。 ■基数:数制所使用的数码个数称为“基数” 或 “基”,常用“R”表示,称R进制。如二进制的数码 是:0、1,基为2。 ■位权:指数码在不同位置上的权值。在进位计数制中, 处于不同数位的数码,代表的数值不同
几个名词术语 ◼ 数码:一组用来表示某种数制的符号。如: 1、2、3、 4、A、B、C等。 ◼ 基数:数制所使用的数码个数称为“基数” 或 “基”,常用“R”表示,称R进制。如二进制的数码 是:0、1,基为2。 ◼ 位权:指数码在不同位置上的权值。在进位计数制中, 处于不同数位的数码,代表的数值不同
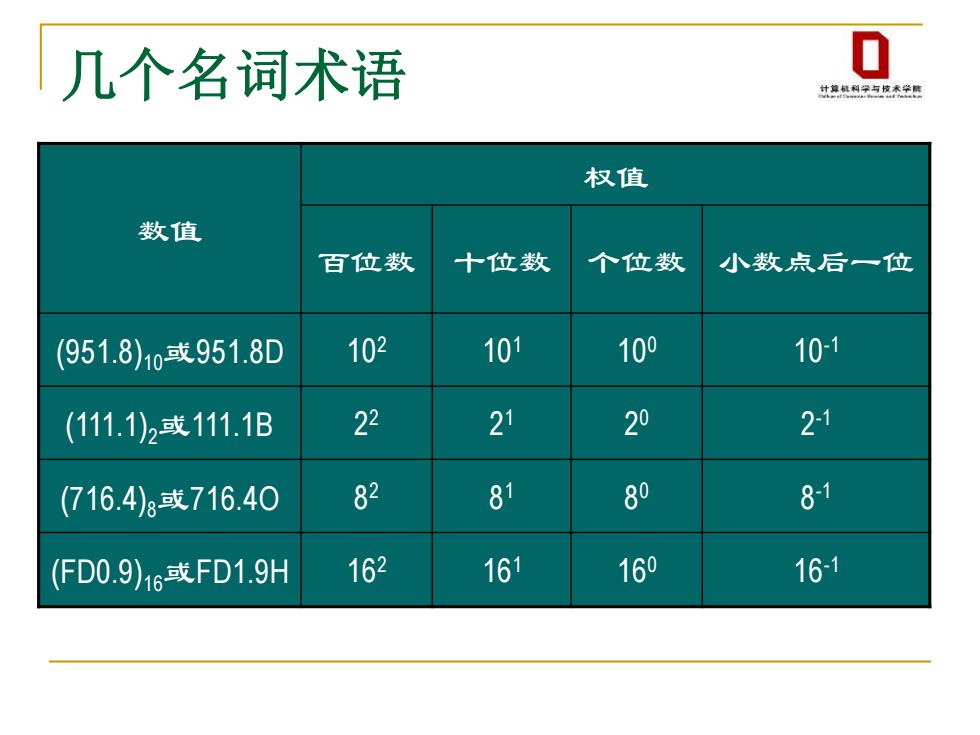
几个名词术语 0 计草机利学与校术学腐 权值 数值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (111.1)2或111.1B 22 21 20 21 (716.4)8或716.40 82 81 80 81 (FD0.9)16或FD1.9H 162 161 160 161
几个名词术语 数值 权值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (111.1)2或111.1B 2 2 2 1 2 0 2 -1 (716.4)8或716.4O 8 2 8 1 8 0 8 -1 (FD0.9)16或FD1.9H 162 161 160 16-1

进位计数制 什草凤利学与拉未学脑 678.34=6×1024⑦×⑩+8×100+3×1044×10-2 数码 基数 权 R进制数用个基本符号(例如0,1,2,一1)表示数值 r进制数N可表示为: N=an-1Xrm-1+an-2Xr-2+.+aoXr0+a_1Xr-1+.+a-Xrm
进位计数制 = =− − a r i i m n i 1 N=an-1×r n-1+an-2×r n-2+.+a0×r 0+a-1×r -1+.+a-m×r -m r进制数N可表示 为: R进制数用 r个基本符号(例如0,1,2,.,r-1)表示数值 数码 基数 权 678.34=6×102+7×101+8×100 +3×10-1+4×10-2