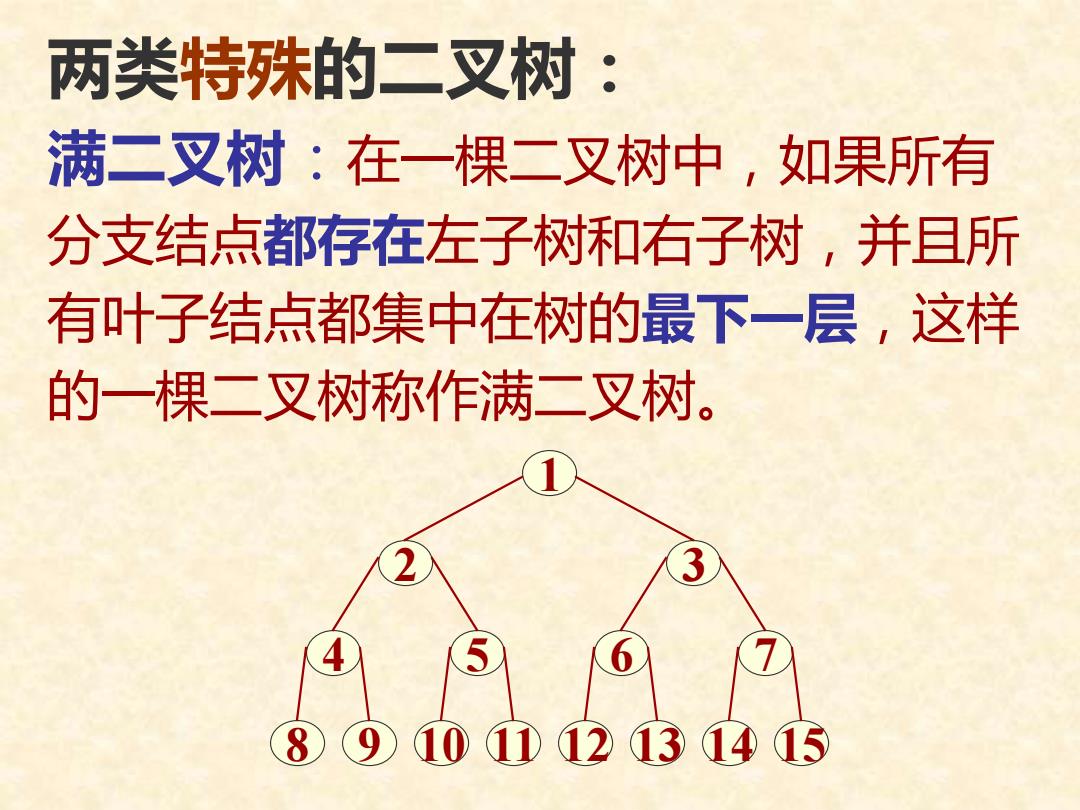
两类特殊的二叉树: 满二叉树:在一棵二叉树中,如果所有 分支结点都存在左子树和右子树,并且所 有叶子结点都集中在树的最下一层,这样 的一棵二叉树称作满二叉树。 101112131415
两类特殊的二叉树: 满二叉树:在一棵二叉树中,如果所有 分支结点都存在左子树和右子树,并且所 有叶子结点都集中在树的最下一层,这样 的一棵二叉树称作满二叉树。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
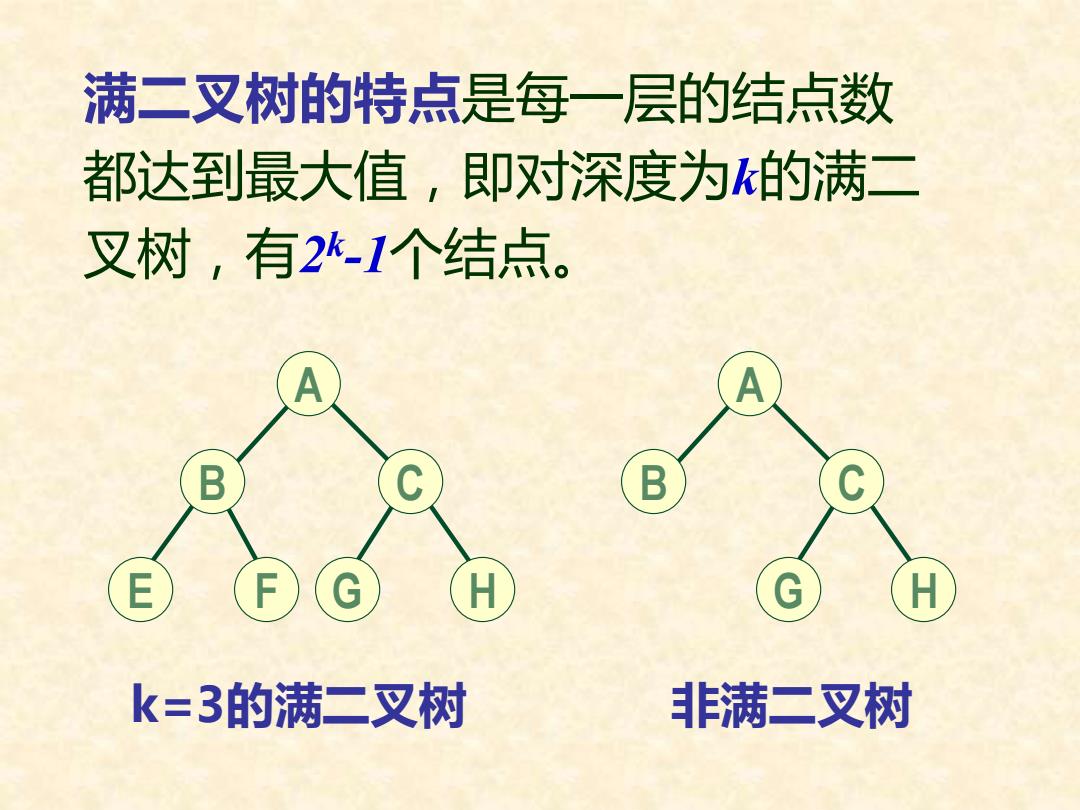
满二叉树的特点是每一层的结点数 都达到最大值,即对深度为的满二 叉树,有21个结点。 A E H H k=3的满二叉树 非满二叉树
k=3的满二叉树 A B C E F G H 非满二叉树 A B C G H 满二叉树的特点是每一层的结点数 都达到最大值,即对深度为k的满二 叉树,有2 k -1个结点
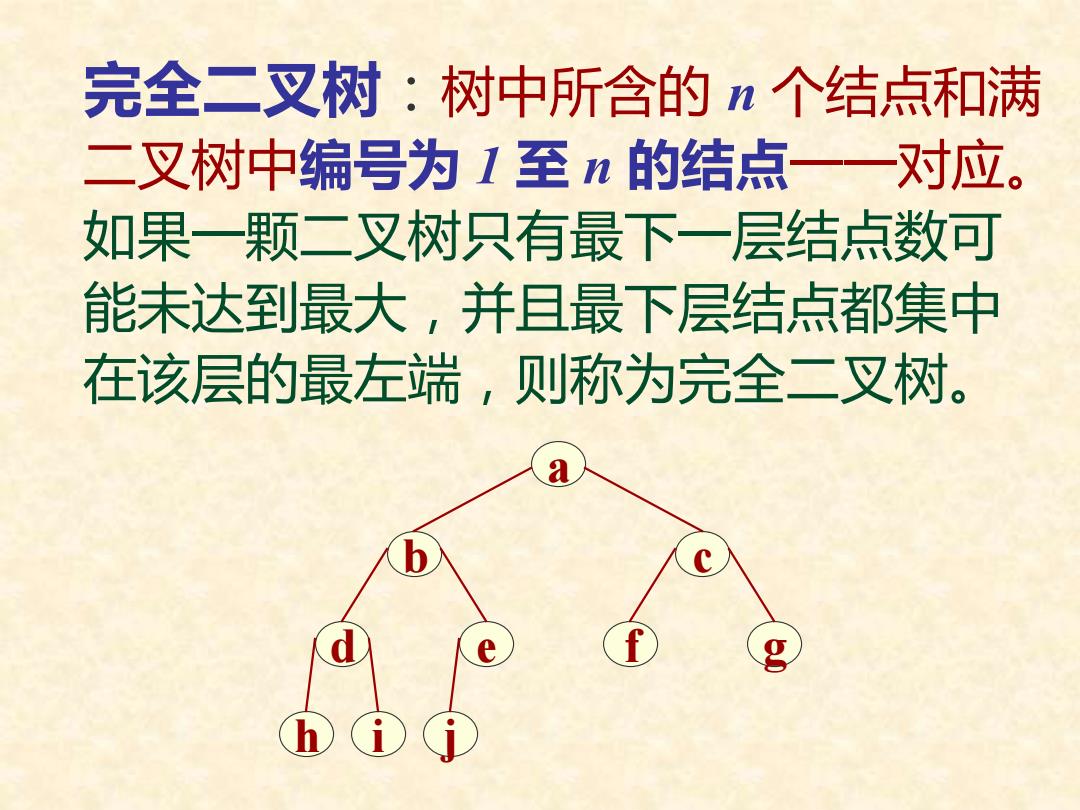
完全二叉树:树中所含的n个结点和满 二叉树中编号为1至n的结点一一对应。 如果一颗二叉树只有最下一层结点数可 能未达到最大,并且最下层结点都集中 在该层的最左端,则称为完全二叉树。 e g
完全二叉树:树中所含的 n 个结点和满 二叉树中编号为 1 至 n 的结点一一对应。 如果一颗二叉树只有最下一层结点数可 能未达到最大,并且最下层结点都集中 在该层的最左端,则称为完全二叉树。 a b c d e f g h i j

完全二叉树的特点是:叶子结点只能出现 在最下层和次下层,也就是说至多是最下面 的两层上结点的度数可以小于2,且最下层的 叶子结点集中在树的左部。显然,一棵满二 叉树必定是一棵完全二叉树,而完全二叉树 未必是满二叉树。 H (a) (b) (c) (a)、(b)完全二叉树 (c)不是完全二叉树
完全二叉树的特点是:叶子结点只能出现 在最下层和次下层,也就是说至多是最下面 的两层上结点的度数可以小于2,且最下层的 叶子结点集中在树的左部。显然,一棵满二 叉树必定是一棵完全二叉树,而完全二叉树 未必是满二叉树。 (a) A B C E F G H (a)、(b)完全二叉树 (c)不是完全二叉树 A B C E F A B C E F H (b) (c)

性质4: 具有n个结点的完全二叉树的深度为 Llog2n/+1。 证明: 设完全二叉树的深度为k 则根据第二条性质得2k1≤n <2k 即k-1≤log2n<k 因为k只能是整数,因此,k=llog2n/+1
性质 4 : 具有 n 个结点的完全二叉树的深度为 log2n +1 。 证明: 设完全二叉树的深度为 k 则根据第二条性质得 2 k-1≤ n < 2 k 即 k-1 ≤ log2 n < k 因为 k 只能是整数,因此, k =log2n + 1