授课教案 第四章光辐射在介质波导中的传播 B 禁区 @cu 0c2 图4.10平板波导B对0关系曲线 (1)禁区:对应B>n,k。传播常数B的最大可能值为Bx=nk。,所以B>n,ko 不可能存在。 (2)导模:对应mk。>B>n,k。,具有离散谱分布。 (3)辐射模:对应B<n,k。,具有连续谱分布。 三、导模的截止 导模截止:日=2,B=n,k,下界面处于全反射临界状态,将进入辐射模状态。 导模截止状态的平板波导特征方程: n2-n)2kd=mπ+p (4.12) 1.模式数量 M=2头m-i)-pi (4.13) 2.第m阶导模的截止频率 0.s cπ () (4.14) d(n) 3.第m阶导模的截止厚度 de= n+p% (4.15) 2(m2-n2)2 维持单模传输的最大厚度
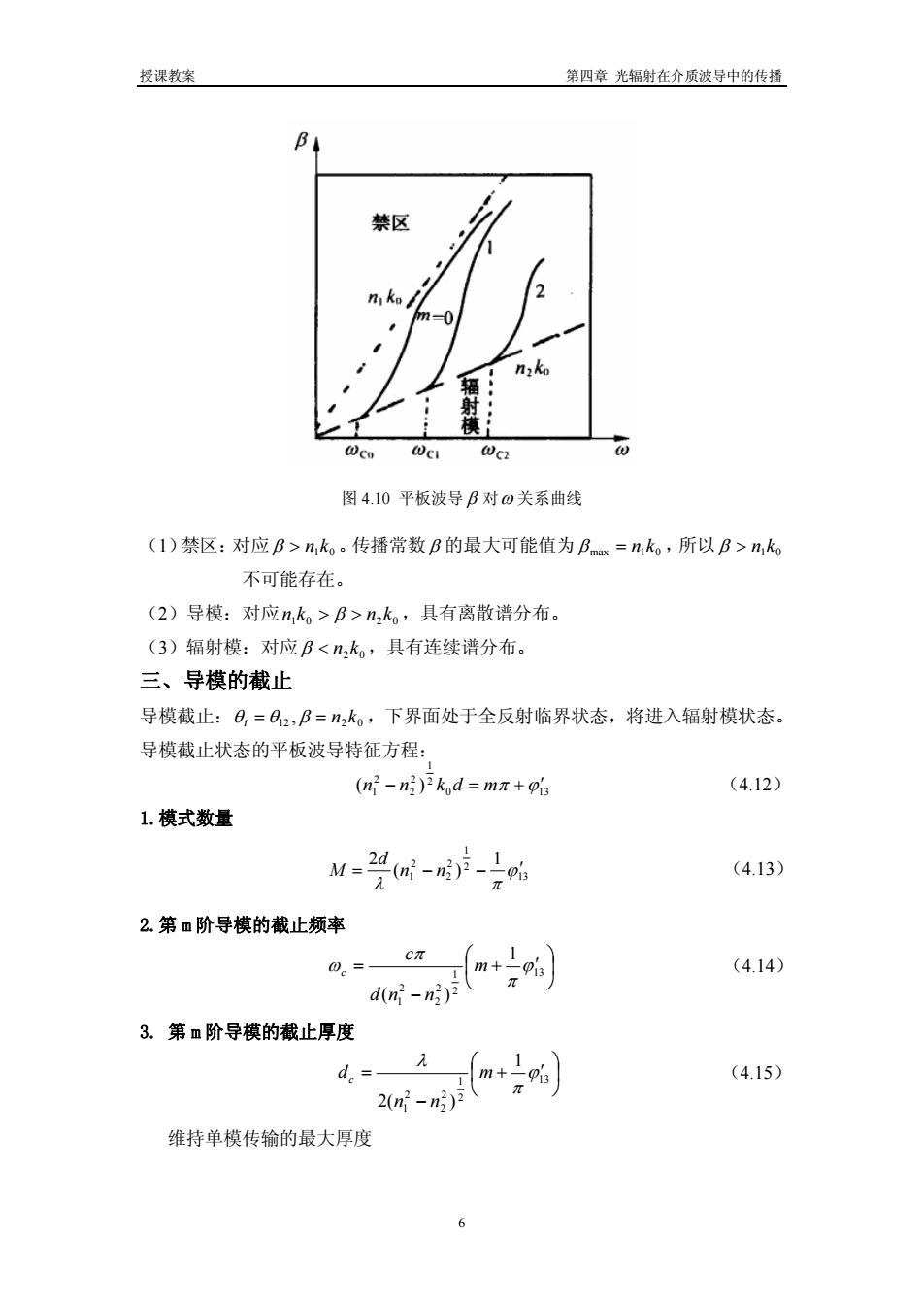
授课教案 第四章 光辐射在介质波导中的传播 图 4.10 平板波导 β 对ω 关系曲线 (1)禁区:对应 01 β > kn 。传播常数β 的最大可能值为 max 01 β = kn ,所以 01 β > kn 不可能存在。 (2)导模:对应 01 02 β >> knkn ,具有离散谱分布。 (3)辐射模:对应 02 β < kn ,具有连续谱分布。 三、导模的截止 导模截止: 12 02 θ i θ ,β == kn ,下界面处于全反射临界状态,将进入辐射模状态。 导模截止状态的平板波导特征方程: 0 13 2 1 2 2 2 1 − )( mdknn += ϕπ ′ (4.12) 1.模式数量 13 2 1 2 2 2 1 1 )( 2 ϕ λ π nn −−= ′ d M (4.13) 2.第 m 阶导模的截止频率 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ′ − = 13 2 1 2 2 2 1 1 )( ϕ π π ω m nnd c c (4.14) 3. 第 m 阶导模的截止厚度 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ′ − = 13 2 1 2 2 2 1 1 )(2 ϕ π λ m nn dc (4.15) 维持单模传输的最大厚度 6

授深教案 第四章光辐射在介质波导中的传福 (4.16) 2(n2-m)2N 维持单模传输的最小厚度 =- (4.17) 维持单一零阶模传输的厚度条件 dmn<d<dm (4.18) 若平板波导为对称结构,则有d。→0,dma=0,0。=0,1→o。 注:对称结构平板波导中,任意波长的光波都能以基模或零阶模的形式传播。 四、渐变折射率平板波导 波失量: k(x)=n(x)k。 k =n(x)ko cos(x) (4.19) k.=B=nx)k。sin(x) 在拐点处k(x)无x分量,B=n(x)k。=n(x2)k。 注:B是与x无关的常数,即aB/a=0。 X◆ 包层 X2 2 no n(x) 0 蛇形光线 衬底 (a)折射率分布 (b)光线轨迹 图4.11对称渐变折射率平板波导 包层 n(x) 弧形光线 衬底 X (a)折射率分布 (化)光线轨迹 图4.12非对称渐变折射率平板波导 >
授课教案 第四章 光辐射在介质波导中的传播 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ′ − = 13 2 1 2 2 2 1 max 1 1 )(2 ϕ π λ nn d (4.16) 维持单模传输的最小厚度 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′ − = 13 2 1 2 2 2 1 min 1 )(2 ϕ π λ nn d (4.17) 维持单一零阶模传输的厚度条件 min < < ddd max (4.18) 若平板波导为对称结构,则有 c → dd min = ωc = ,0,0,0 λ → ∞ 。 注:对称结构平板波导中,任意波长的光波都能以基模或零阶模的形式传播。 四、渐变折射率平板波导 波失量: ⎪ ⎩ ⎪ ⎨ ⎧ == = = )(sin)( )(cos)( )()( 0 0 0 xkxnk xkxnk kxnxk z x β θ θ (4.19) 在拐点处 无 x 分量, xk )( 01 02 β = = )()( kxnkxn 。 注: β 是与 x无关的常数,即∂β ∂x = 0 。 (a)折射率分布 (b)光线轨迹 图 4.11 对称渐变折射率平板波导 (a)折射率分布 (b)光线轨迹 图 4.12 非对称渐变折射率平板波导 7
授课教案 第四章光辐射在介质波导中的传播 §4-3光纤中的射线分析 一、概述 保护套 涂敷层 纤芯 图4.13光纤剖面结构图 按折射率分布分类阶跃(突变)光纤 孔渐变光纤 按传输模式分类单模光纤 多模光纤 横截面 折射率分布 输入脉冲 光线传播路径 输出脉冲 闵引 HOp. 图4.14三种基本类型的光纤 (a)阶跃型多模光纤;)渐变型多模光纤;(c)单模光纤 为调整工作波长或改善色散特性,可以在图4.14(c)常规单模光纤的基础上, 设计许多结构复杂的特种单模光纤。最有用的若干典型特种单模光纤的横截面结 构和折射率分布示于图4.15
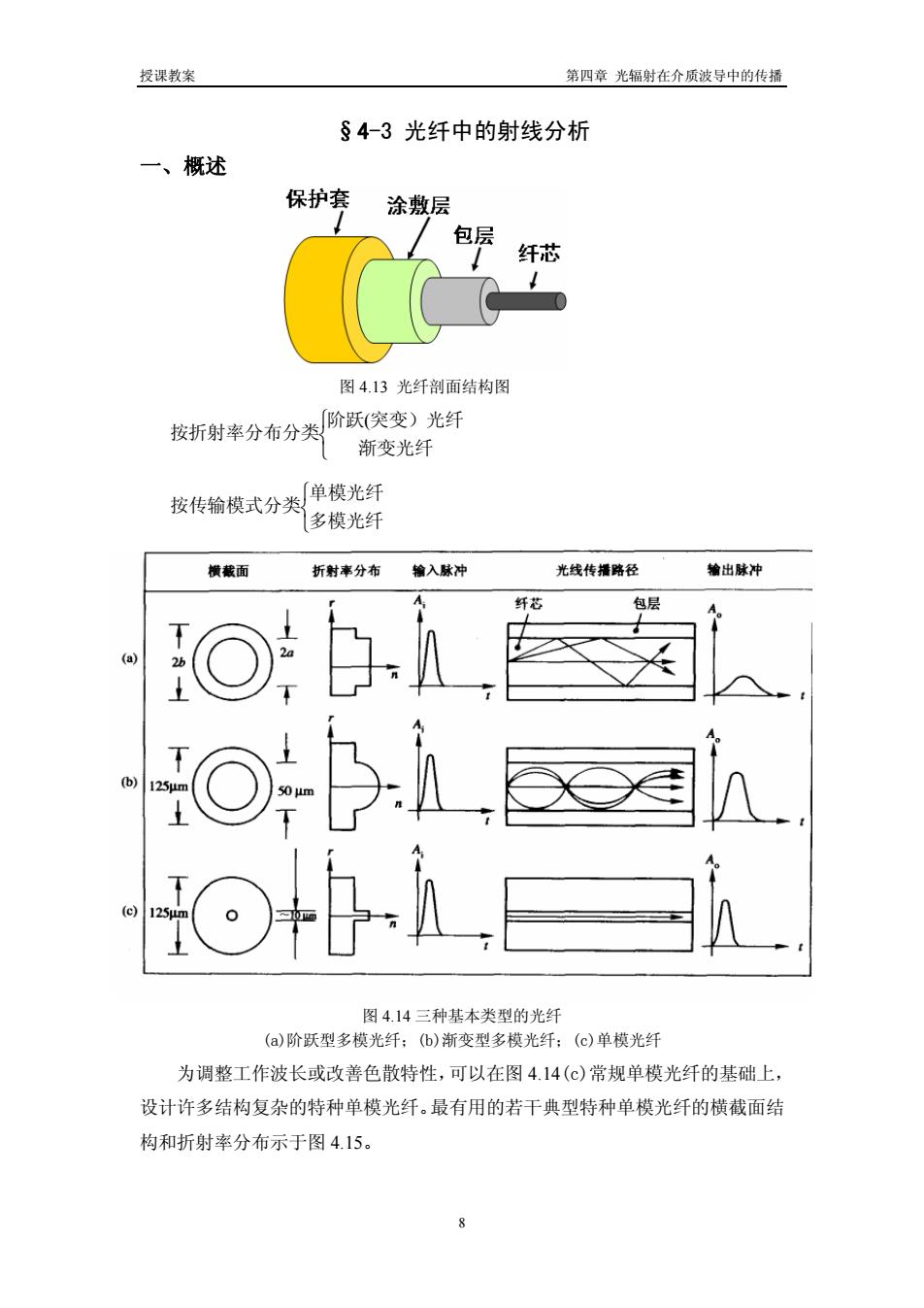
授课教案 第四章 光辐射在介质波导中的传播 §4-3 光纤中的射线分析 一、概述 图 4.13 光纤剖面结构图 ⎩ ⎨ ⎧ 渐变光纤 阶跃 突变)光纤 按折射率分布分类 ( ⎩ ⎨ ⎧ 多模光纤 单模光纤 按传输模式分类 图 4.14 三种基本类型的光纤 (a)阶跃型多模光纤;(b)渐变型多模光纤;(c)单模光纤 为调整工作波长或改善色散特性,可以在图 4.14(c)常规单模光纤的基础上, 设计许多结构复杂的特种单模光纤。最有用的若干典型特种单模光纤的横截面结 构和折射率分布示于图 4.15。 8

授误教案」 第四章光辐射在介质波导中的传播 双包层光纤:折射率分布像W形,又称为W型光纤。这种光纤有两个包层, 内包层外直径2a'与纤芯直径2a的比值a'/a≤2。适当选取纤芯、外包层和内 包层的折射率n1、n2和n,调整a值,可以得到在1.3l.6m之间色散变化很小 的色散平坦光纤,或把零色散波长移到1.55m的色散移位光纤。 三角芯光纤:纤芯折射率分布呈三角形,这是一种改进的色散移位光纤。这 种光纤在1.55m有微量色散,有效面积较大,适合于密集波分复用和孤子传输 的长距离系统使用,康宁公司称它为长距离系统光纤,这是一种非零色散光纤 椭圆芯光纤:纤芯折射率分布呈椭圆形。这种光纤具有双折射特性,即两个 正交偏振模的传输常数不同。强双折射特性能使传输光保持其偏振状态,因而又 称为双折射光纤或偏振保持光纤。 (a) (b) (b) 图4.15典型单模特种光纤 (a)双包层b)三角芯(c)椭圆芯 以上各种特征不同的光纤,其用途也不同。突变型多模光纤信号畸变大,相 应的带宽只有10~20 MHzkm,只能用于小容量(8Mb/s以下)短距离(儿km以内) 系统。渐变型多模光纤的带宽可达1~2 GHzkm,适用于中等容量(34-140Mb/s) 中等距离(10-20km)系统。大容量(622Mb/s-2.5Gbs)长距离(30km以上)系 统都要使用单模光纤。 二、阶跃光纤的射线理论 1.子午线与子午面 子午线:光纤在传播时始终在同一个包含光纤轴线的平面内。子午线在光纤端 面的投影是一条直径。 子午面:包含子午线的平面
授课教案 第四章 光辐射在介质波导中的传播 双包层光纤:折射率分布像 W 形,又称为 W 型光纤。这种光纤有两个包层, 内包层外直径 2a’与纤芯直径 2 a 的比值 ′ aa ≤ 2/ 。适当选取纤芯、外包层和内 包层的折射率 、 和 n1 n2 n3,调整 a 值,可以得到在 1.3~1.6 μm之间色散变化很小 的色散平坦光纤,或把零色散波长移到 1.55 μm的色散移位光纤。 三角芯光纤:纤芯折射率分布呈三角形,这是一种改进的色散移位光纤。这 种光纤在 1.55 μm有微量色散,有效面积较大,适合于密集波分复用和孤子传输 的长距离系统使用,康宁公司称它为长距离系统光纤,这是一种非零色散光纤。 椭圆芯光纤:纤芯折射率分布呈椭圆形。这种光纤具有双折射特性,即两个 正交偏振模的传输常数不同。强双折射特性能使传输光保持其偏振状态,因而又 称为双折射光纤或偏振保持光纤。 图 4.15 典型单模特种光纤 (a) 双包层(b) 三角芯(c) 椭圆芯 以上各种特征不同的光纤,其用途也不同。突变型多模光纤信号畸变大,相 应的带宽只有 10~20MHz·km,只能用于小容量(8Mb/s 以下)短距离(几 km 以内) 系统。渐变型多模光纤的带宽可达 1~2GHz·km,适用于中等容量(34~140Mb/s) 中等距离(10~20km)系统。大容量(622 Mb/s~2.5Gb/s)长距离(30 km 以上)系 统都要使用单模光纤。 二、阶跃光纤的射线理论 1.子午线与子午面 子午线:光纤在传播时始终在同一个包含光纤轴线的平面内。子午线在光纤端 面的投影是一条直径。 子午面:包含子午线的平面。 9
授课教案 第四章光辐射在介质波导中的传播 图4.16光纤中的子午射线 2.相对折射率差 相对折射率差△定义为 4=1-(2)21/2 (4.20) 当4<0.01时,上式简化为 4乃-% (4.21) 3.数值孔径 纤芯折射率:m:包层折射率:n2:空气折射率:。=1。光线在光纤端面入 射角:0:折射角:日,折射后的光线在纤芯直线传播,并在纤芯与包层交界面 以角度0入射到包层(m>n2)。 2 图4.17光纤的数值孔径NA n 、L最短 L最长 260 图4.18不同入射角的光线产生时延差示意图 由全反射定律可知存在一临界角p。(p。=arcsin(m,/m,)
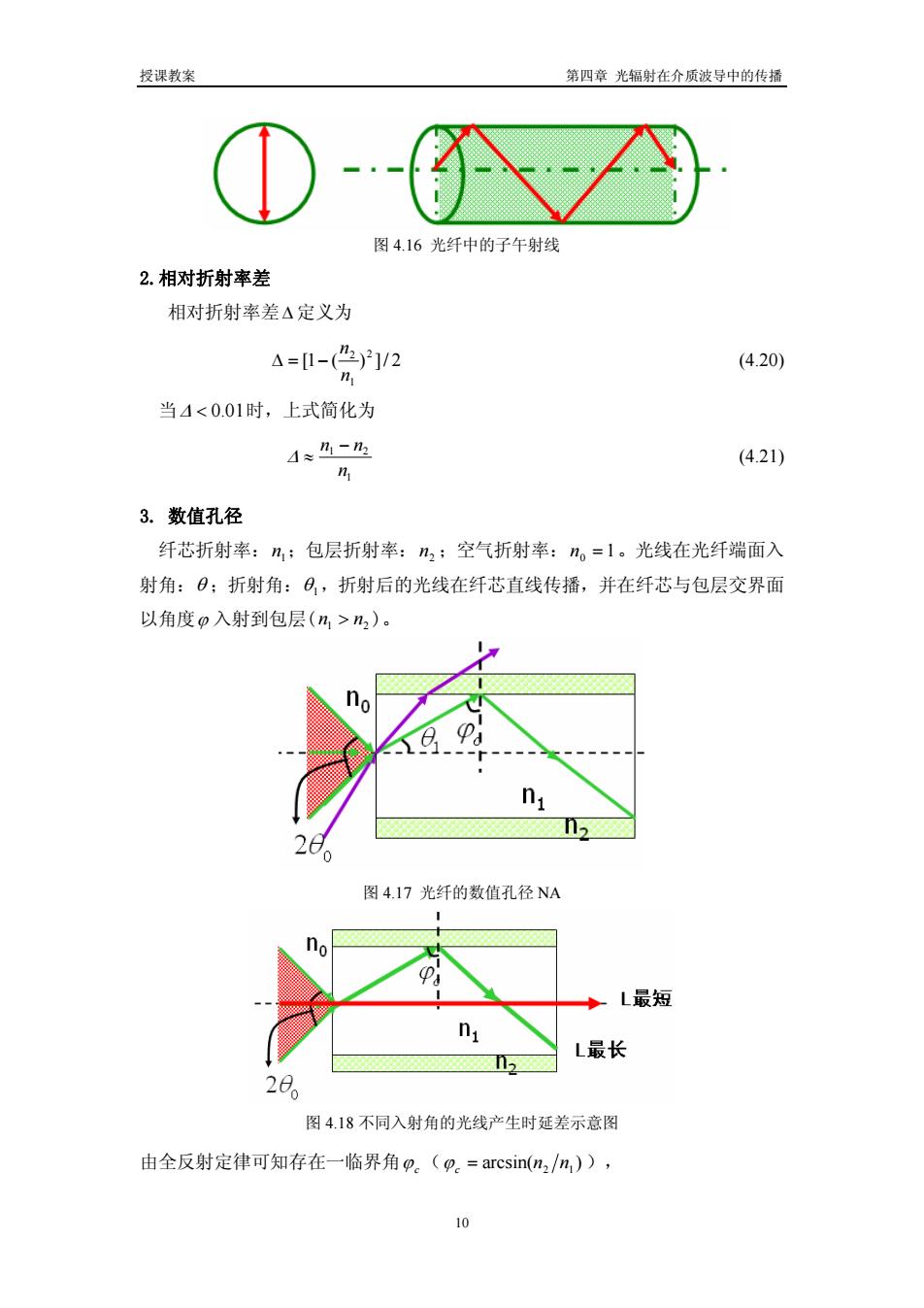
授课教案 第四章 光辐射在介质波导中的传播 图 4.16 光纤中的子午射线 2.相对折射率差 相对折射率差Δ 定义为 2/])(1[ 2 1 2 n n −=Δ (4.20) 当Δ < 01.0 时,上式简化为 1 21 n − nn Δ ≈ (4.21) 3. 数值孔径 纤芯折射率: ;包层折射率: ;空气折射率: 1 n 2 n n0 = 1。光线在光纤端面入 射角:θ ;折射角:θ1,折射后的光线在纤芯直线传播,并在纤芯与包层交界面 以角度ϕ 入射到包层( )。 21 > nn 图 4.17 光纤的数值孔径 NA 图 4.18 不同入射角的光线产生时延差示意图 由全反射定律可知存在一临界角ϕ c ( arcsin( ) ϕc = nn 12 ), 10