建立 样本线性回归方程的方法 最小二乘法 实际观察值与样本回归线上 的点的距离的平方和最小 x y e1 e2 e3 e4 y y i i i n i i n e − = = = 1 2 2 1 最小
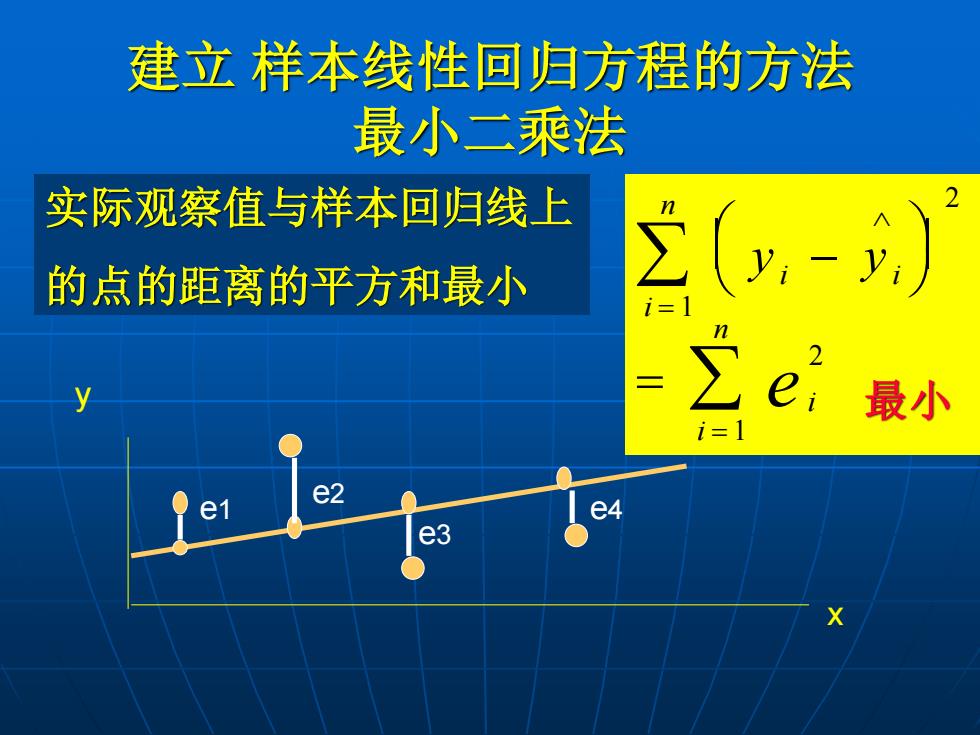
建立 样本线性回归方程的方法 最小二乘法 实际观察值与样本回归线上 的点的距离的平方和最小 x y e1 e2 e3 e4 y y i i i n i i n e − = = = 1 2 2 1 最小

、b应使回归估计值 与实际观测值 y的偏差平方和最小,即:总的离回归平 方和,即剩余平方和 y ˆ 根据微积分学中的求极值的方法,令 Q对a、b的一阶偏导数等于0,即: = − = − − = 2 2 Q (y y ˆ) (y a bx) 最小 (6-3) (6-4) a ( ) ( ) = − − + = = − − + = = = 2 0 2 0 1 1 n i i i i n i i i y a bx x b Q y a bx a Q
、b应使回归估计值 与实际观测值 y的偏差平方和最小,即:总的离回归平 方和,即剩余平方和 y ˆ 根据微积分学中的求极值的方法,令 Q对a、b的一阶偏导数等于0,即: = − = − − = 2 2 Q (y y ˆ) (y a bx) 最小 (6-3) (6-4) a ( ) ( ) = − − + = = − − + = = = 2 0 2 0 1 1 n i i i i n i i i y a bx x b Q y a bx a Q

经整理,得关于a、b的正规方程组: 上一张 下一张 主 页 退 出 解正规方程组,得: x xy SS SP x x x x y y x x n x y x y n b = − − − = − − = 2 2 2 ( ) ( )( ) ( ) / ( )( )/ a = y −bx (6-5) (6-7) = + + = = = = = = n i i i n i i n i i n i i n i i a x x b x y na b x y 1 1 2 1 1 1
经整理,得关于a、b的正规方程组: 上一张 下一张 主 页 退 出 解正规方程组,得: x xy SS SP x x x x y y x x n x y x y n b = − − − = − − = 2 2 2 ( ) ( )( ) ( ) / ( )( )/ a = y −bx (6-5) (6-7) = + + = = = = = = n i i i n i i n i i n i i n i i a x x b x y na b x y 1 1 2 1 1 1

在6-7式中,分子为自变量x的离均差与 依变量y的离均差的乘积和 , 简称乘积和,记作 ,分母是自变量x的离 均差平方和 ,记作SSX。 (x − x)( y − y) xy SP − 2 (x x) x xy SS SP x x x x y y b = − − − = 2 ( ) ( )( ) a = y −bx 所 以
在6-7式中,分子为自变量x的离均差与 依变量y的离均差的乘积和 , 简称乘积和,记作 ,分母是自变量x的离 均差平方和 ,记作SSX。 (x − x)( y − y) xy SP − 2 (x x) x xy SS SP x x x x y y b = − − − = 2 ( ) ( )( ) a = y −bx 所 以

a为回归截距(regression intercept),是回归 直线与y轴交点的纵坐标,当x=0时, ; b为回归系数(regression coefficient),表示x变 化一个单位,y平均变化的数量;b的符号反 映了x影响y的性质,b的绝对值大小反映了x 影响y的程度; 为回归估计值,是当x在其 研究范围内取某一个值时,y值平均数 的估计值。 y ˆ + x y ˆ =a y ˆ =E(y)=E( + x)
a为回归截距(regression intercept),是回归 直线与y轴交点的纵坐标,当x=0时, ; b为回归系数(regression coefficient),表示x变 化一个单位,y平均变化的数量;b的符号反 映了x影响y的性质,b的绝对值大小反映了x 影响y的程度; 为回归估计值,是当x在其 研究范围内取某一个值时,y值平均数 的估计值。 y ˆ + x y ˆ =a y ˆ =E(y)=E( + x)