安徽理工大学：《人工智能原理》课程教学资源（课件讲稿）人工神经网络 ANN

第九章人工神经网络 安徽理工大学计算机学院方贤进 (春季，研究生课程) 神经网络是通过模拟人脑的结构和工作模式，使机器具有类似人类的智 能，如机器学习、知识获取、专家系统等。 9.1人工神经网络的概念、结构 人工神经网络(Artificial Neural Nets,ANN)是由大量处理单元经广泛互连 而组成的人工网络，用来模拟脑神经系统的结构和功能。而这些处理单元称作人 工神经元。 人工神经网络(AN)可以看成是以人工神经元为结点，用有向加权弧连接起来 的有向图。在此有向图中，人工神经元就是对生物神经元的模拟，而有向弧则是 轴突一突触一树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相 互作用的强弱。 人工神经网络的组成： w2 8 w3

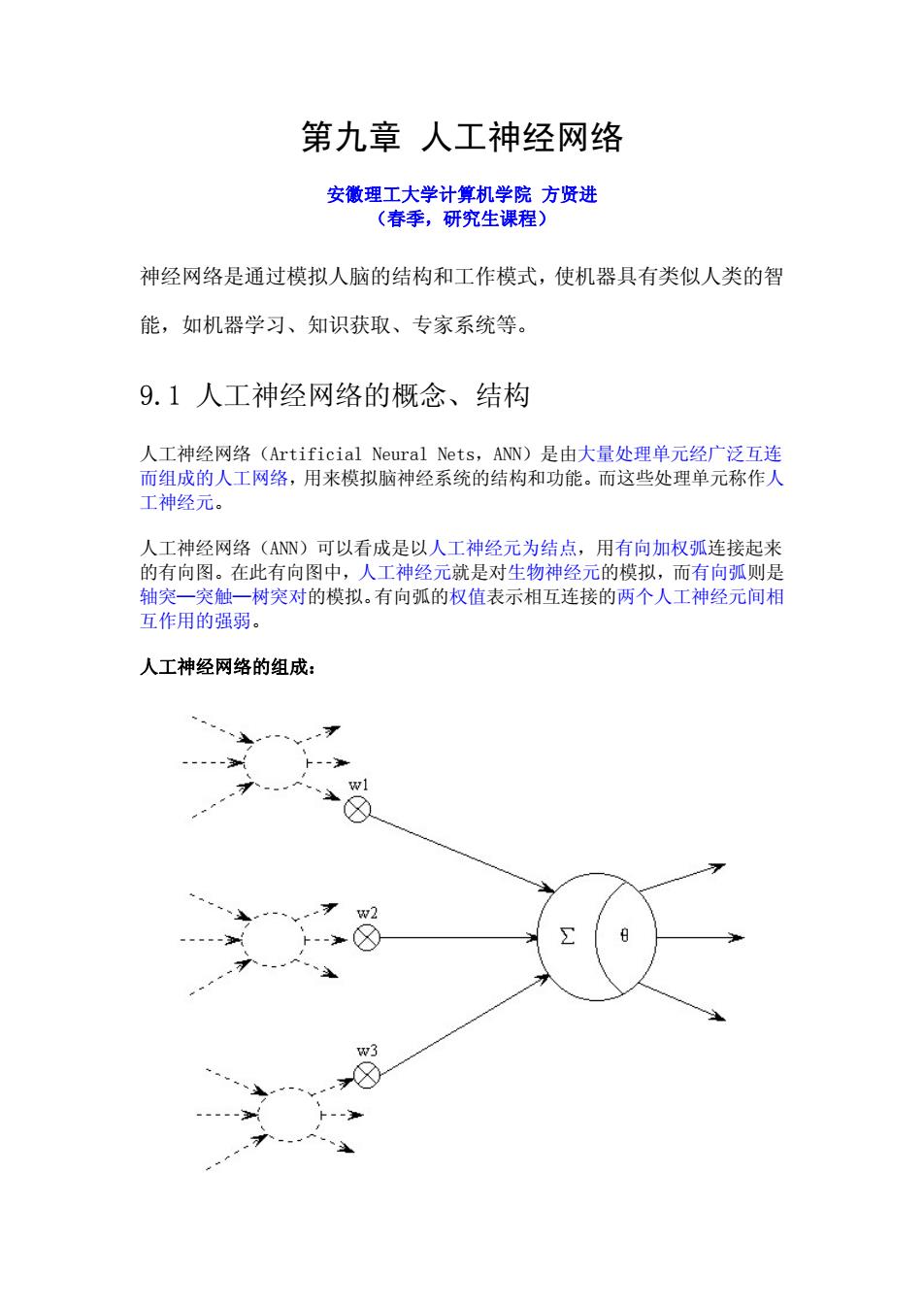
第九章 人工神经网络 安徽理工大学计算机学院 方贤进 （春季，研究生课程） 神经网络是通过模拟人脑的结构和工作模式，使机器具有类似人类的智 能，如机器学习、知识获取、专家系统等。 9.1 人工神经网络的概念、结构 人工神经网络（Artificial Neural Nets，ANN）是由大量处理单元经广泛互连 而组成的人工网络，用来模拟脑神经系统的结构和功能。而这些处理单元称作人 工神经元。 人工神经网络（ANN）可以看成是以人工神经元为结点，用有向加权弧连接起来 的有向图。在此有向图中，人工神经元就是对生物神经元的模拟，而有向弧则是 轴突—突触—树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相 互作用的强弱。 人工神经网络的组成：

人工神经元模型由心理学家Mcculloch和数理逻辑学家Pitts合作提出的M-P 模型： w1 下2 w2 8 wn x,x2,··,X是来自其它人工神经元的信息作为该人工神经元的输入，权值 W,W2,.,W表示各输入的连接强度。0是神经元兴奋时的内部阈值，当神经元 输入的加权和大于0时，神经元处于兴奋状态。而神经元的输出为： y=J f称为激发函数或作用函数，该输出为1或0取决于其 输入之和大于或小于内部阈值。也就是说令： 2 ∑- i=0 ,f函数的定义如下 1,6>0 y=f(o)= 0,6<0 即σ>0时，该神经元被激活，进入兴奋状态，f(o)=1,当o<0时，该神经元被 抑制，f(o)=0 激发函数具有非线性特性。常用的非线性激发函数有阈值型、分段线性型、 Sigmoid函数型（简称S型）和双曲正切型。如下图所示：

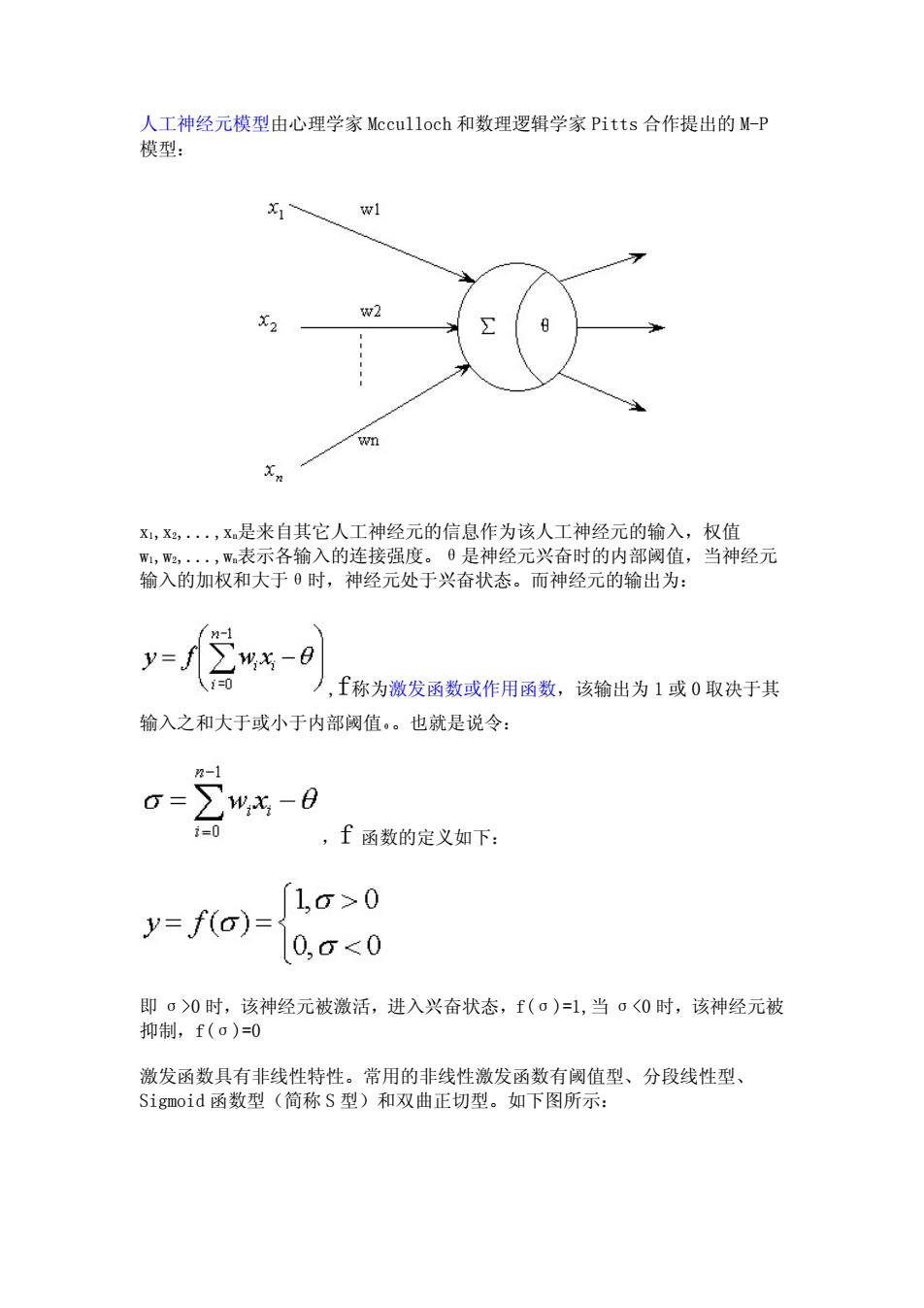
人工神经元模型由心理学家 Mcculloch 和数理逻辑学家 Pitts 合作提出的 M-P 模型： x1,x2,...,xn是来自其它人工神经元的信息作为该人工神经元的输入，权值 w1,w2,...,wn表示各输入的连接强度。θ是神经元兴奋时的内部阈值，当神经元 输入的加权和大于θ时，神经元处于兴奋状态。而神经元的输出为： ,f称为激发函数或作用函数，该输出为1或0 取决于其 输入之和大于或小于内部阈值θ。也就是说令： ，f 函数的定义如下： 即 σ>0 时，该神经元被激活，进入兴奋状态，f(σ)=1,当 σ<0 时，该神经元被 抑制，f(σ)=0 激发函数具有非线性特性。常用的非线性激发函数有阈值型、分段线性型、 Sigmoid 函数型（简称 S 型）和双曲正切型。如下图所示：

io) f(o 阈值型 分段线性 f(o) f(o) .1 Sigmoid函数型 双曲正切型 9.2单层感知器(Perceptron)模型及其学习算法 9.2.1感知器训练法则 1957年美国学者Rosenblatt提出了一类具有自学习能力的感知器模型，它是一 个具有单层计算单元的前向神经网络，其神经元为线性阈值单元，称为单层感知 器。它和M-P模型相似，当输入信息的加权和大于或等于阈值时，输出为1，否 则输出为0或-1。与M-P模型不同之处是神经元之间的连接权值W是可变的，这 种可变性就保证了感知器具有学习能力。 Rosenblatt提出的单层感知器由输入部分和输出层构成，输出层即为它的计算 层。在该感知器模型中，输入部分和输出层都可由多个神经元（处理单元）构成， 输入部分的神经元与输出层的各种神经元间均有连接。当输入部分将输入数据传 送给连接的处理单元时，输出层就会对所有输入数据进行加权求和，经阈值型作 用函数产生一组输出数据

9.2 单层感知器（Perceptron）模型及其学习算法 9.2.1 感知器训练法则 1957 年美国学者Rosenblatt提出了一类具有自学习能力的感知器模型，它是一 个具有单层计算单元的前向神经网络，其神经元为线性阈值单元，称为单层感知 器。它和M-P模型相似，当输入信息的加权和大于或等于阈值时，输出为 1，否 则输出为 0 或-1。与M-P模型不同之处是神经元之间的连接权值wi是可变的，这 种可变性就保证了感知器具有学习能力。 Rosenblatt 提出的单层感知器由输入部分和输出层构成，输出层即为它的计算 层。在该感知器模型中，输入部分和输出层都可由多个神经元（处理单元）构成， 输入部分的神经元与输出层的各种神经元间均有连接。当输入部分将输入数据传 送给连接的处理单元时，输出层就会对所有输入数据进行加权求和，经阈值型作 用函数产生一组输出数据

81 W 1 x2 ym 输入部分一 输出层 1, 若∑%，-日，20 到 y=1 0, 若∑州-日，<0 Jj=1,2,,m 1959年Rosenblatt提出了感知器模型中连接权值参数的学习算法。算法的思想 是首先把连接权值和阈值初始化为较小的非零随机数，然后把有个连接权值的 输入送入网络，经加权运算处理，得到的输出如果与所期望的输出有较大的差别， 就对连接权值参数按照某种算法进行自动调整，经过多次反复，直到所得到 的输出与所期望的输出间的差别满足要求为止。 感知器信息处理的规则为： 其中y(t)为t时刻输出，xi为输入向量的一个分量，Wi(t)为t时刻第i个输入 的加权，0为阈值，f0为阶跃函数。 感知器的学习规则如下： W(1+1)=W(t)+nd-xt)k 其中n为学习率(0<n<1),d为期望输出，y(t)为实际输出

1959 年 Rosenblatt 提出了感知器模型中连接权值参数的学习算法。算法的思想 是首先把连接权值和阈值初始化为较小的非零随机数，然后把有 n 个连接权值的 输入送入网络，经加权运算处理，得到的输出如果与所期望的输出有较大的差别， 就对连接权值参数按照某种算法进行自动调整，经过多次反复，直到所得到 的输出与所期望的输出间的差别满足要求为止。 感知器信息处理的规则为： ， 其中 y(t)为 t 时刻输出，xi 为输入向量的一个分量，Wi(t)为 t 时刻第 i 个输入 的加权，θ 为阈值，f()为阶跃函数。 感知器的学习规则如下： 其中 η 为学习率（0<η<1），d 为期望输出，y(t)为实际输出

单层感知器学习算法(learning algorithm for single layer perceptron): stepl:initialize connection weight and threshold.set a smaller nonzero random value for wi(i=1,...,n)and 0 as their initial value.wi(0)represents connection weight of i-th input at the moment of t; step2:input a training parameter =(x1(t),x2(t),...,xn(tand the expectation output d(t); step3:compute the actual output of ANN: 0=f(②0,0x,(0-6.1=1,2,为 step4:compute the difference value between actual output and expectation output: DEL=d(t)-y(t) if DEL<e (e is a very small positive number),then training of ANN is over,otherwise goto step 5; step5:regulate the connection weight according to the following fomular: m,t+1)=m,⑤+p(d(⑤-⑤)x,,1=1-n where 0<n<=1 is an incremental factor,it is used to control regulation speed,and called learning rate.Usualy,the value of n can't be too large or small.if its value is too large,then n will impact the convergence of wi(t),otherwise make the convergence speed of wi(t)slower: step 6:goto step 2;

单层感知器学习算法(learning algorithm for single layer perceptron)： step1:initialize connection weight and threshold. set a smaller nonzero random value for wi(i=1,...,n) and θ as their initial value. wi(0) represents connection weight of i-th input at the moment of t; step2:input a training parameter X=(x1(t),x2(t),...,xn(t))and the expectation output d(t); step3:compute the actual output of ANN: step4:compute the difference value between actual output and expectation output: DEL=d(t)-y(t) if DEL<ε(ε is a very small positive number), then training of ANN is over, otherwise goto step 5; step5: regulate the connection weight according to the following fomular: where 0<η<=1 is an incremental factor, it is used to control regulation speed, and called learning rate. Usualy, the value of η can't be too large or small. if its value is too large, then η will impact the convergence of wi(t),otherwise make the convergence speed of wi(t) slower; step 6: goto step 2;