
站在叶轮上,在1、2两点间列同一时刻流线柏努利方程,则 2g-4.w3@2 1 p22 82-2)+B-A=7o2-ra2 w2-w2 2 2 u-ui+wi-wi ((u=r@) 2 所以 -+w-w+-c 2 2 2 H-+-w+c- 2g 2g 2g 理论压头(2-4)(P87) 由余弦定理 w2=c2+42-2c41cosa% w=c号+4-2c4cosa2 =- 2C2c0SC2-41C1c0S1 得 8 基本方程(2-5)(P87)
站在叶轮上,在1、2两点间列同一时刻流线柏努利方程,则 所以 ——理论压头(2-4)(P87) 由余弦定理 得 ——基本方程(2-5)(P87)

在离心泵的设计中,一般使o1=90°,则c0s1=0 所以 42C2C0S2 8 cigp,=42-c cosa2 C,2 代入上式,得 uxC.acep 8 又将 er =Cy2nDb2 πD2n 42= 60 代入上式,得 = uetgBer π2Dn2 nctgB2Or gπDb2 3600g 60gb2 6.基本方程的讨论 (1)理论压头与叶轮直径及转速成正比。 (2)叶片的几何形状对理论压头的影响:
在离心泵的设计中,一般使1=90,则cos1=0 所以 将 代入上式,得 又将 代入上式,得 6.基本方程的讨论 (1) 理论压头与叶轮直径及转速成正比。 (2) 叶片的几何形状对理论压头的影响:

a.后弯叶片,B2<90°,ctgp2>0, 8 径向叶片,B2=90°,ctg那2=0, =- 8 穹叶片,阝290°,Cg2<0, u 8 由上可见,B,值越大,H值越高,似乎前弯叶片较好。但由于B,大于90°以后,随邮,的增加, 动压头增加,静压头反而减小,从而能量损失大,效率低。因此,实际上离心泵的叶片总是 后弯的。 (3)理论流量对理论压头的影响 当叶轮的几何尺寸(D2、b2、2)和转速()一定时,理论压头与理论流量呈线性关系。 a. B2>90°,Q↑,HT↑ b. B2=90°,Q↑,Hm→ C. B2<90°,Q个,H↓ H或 Qr或g 实际上,叶轮的叶片数是有限的,液体也是非理想液体,所以实际压头和实际流量的关系曲 线应在理论压头和理论流量的关系曲线的下方。 7.性能参数 (1)流量:单位时间内泵所输送的液体体积,Q,m/s、m/h或Ls。 (2)扬程(压头):单位重量的液体流经泵后所获得的能量,H,液柱。 扬程(一般)由实验测定,装置如图,原理如下:
a. 后弯叶片,290,ctg20, b. 径向叶片,2=90,ctg2=0, C. 前弯叶片,290,ctg20, 由上可见,2值越大,HT值越高,似乎前弯叶片较好。但由于2大于90以后,随2的增加, 动压头增加,静压头反而减小,从而能量损失大,效率低。因此,实际上离心泵的叶片总是 后弯的。 (3) 理论流量对理论压头的影响 当叶轮的几何尺寸(D2、b2、2 )和转速(n)一定时,理论压头与理论流量呈线性关系。 a. 290,QT,HT b. 2=90,QT,HT→ C. 2<90,QT,HT 实际上,叶轮的叶片数是有限的,液体也是非理想液体,所以实际压头和实际流量的关系曲 线应在理论压头和理论流量的关系曲线的下方。 7.性能参数 (1) 流量:单位时间内泵所输送的液体体积,Q,m3 /s、m3 /h或L/s。 (2) 扬程(压头):单位重量的液体流经泵后所获得的能量,H,m液柱。 扬程(一般)由实验测定,装置如图,原理如下: QT或Q HT或H
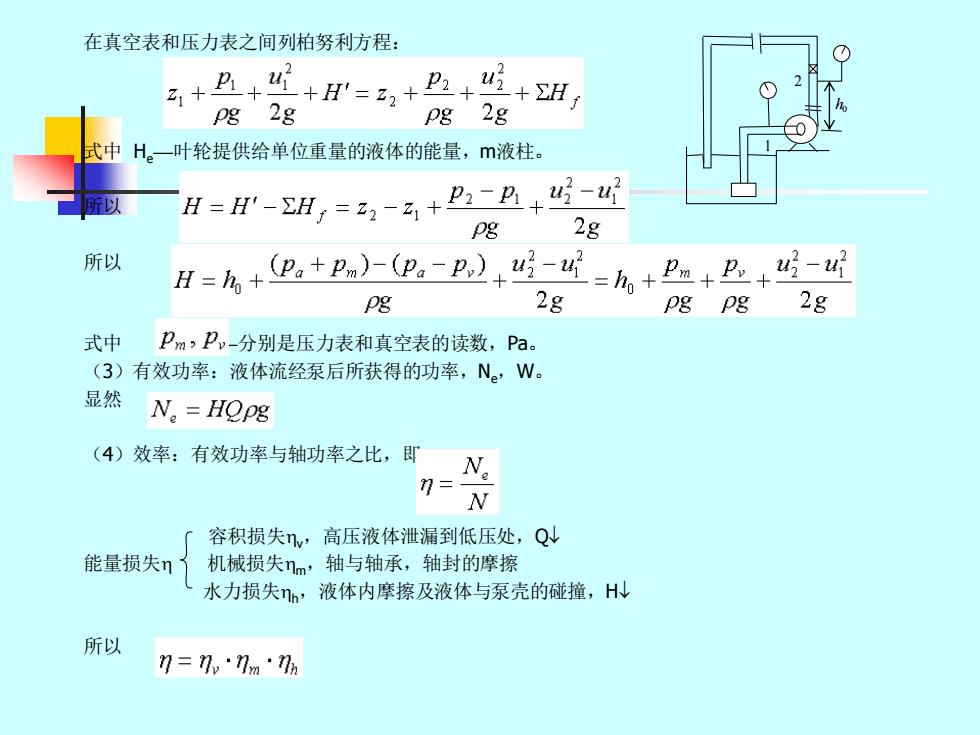
在真空表和压力表之间列柏努利方程: +A++=,+n++H, pg 2g pg 2g 式中H。一叶轮提供给单位重量的液体的能量,m液柱。 所以 H=H-H,=a2-a,+P:-B+5- pg 2g 所以 H=么+B,+P)m,-D)+5-4=h+P+L+ pg 2g pgpg 2g 式中 Pm,P,-分别是压力表和真空表的读数,Pa。 (3)有效功率:液体流经泵后所获得的功率,N。,W。 显然 N。=HQPg (4)效率:有效功率与轴功率之比,即 7= N 容积损失nw,高压液体泄漏到低压处,Q 能量损失n 机械损失nm,轴与轴承,轴封的摩擦 水力损失nh, 液体内摩擦及液体与泵壳的碰撞,HN 所以 7=7,·7m·7h
在真空表和压力表之间列柏努利方程: 式中 He—叶轮提供给单位重量的液体的能量,m液柱。 所以 所以 式中 ——分别是压力表和真空表的读数,Pa。 (3)有效功率:液体流经泵后所获得的功率,Ne,W。 显然 (4)效率:有效功率与轴功率之比,即 容积损失v,高压液体泄漏到低压处,Q 能量损失 机械损失m,轴与轴承,轴封的摩擦 水力损失h,液体内摩擦及液体与泵壳的碰撞,H 所以 1 2 h0