
The samples are independent of each other: w国=wr20=2o- σ2 The variance var(X)can be written in the form of expectation: a网-天=AG-的 Then: s1=2--的=V2,=1-最r The unbiased estimate of sample variance should be: s2=wx- i-1 15/88
▶ The samples are independent of each other: var(X) = var( 1 N X N i=1 Xi) = 1 N2 X N i=1 var(Xi) = σ 2 N . ▶ The variance var(X) can be written in the form of expectation: var(X) = σ 2 N = E[(X − µ) 2 ] Then: E[S 2 ] = σ 2 − E[(X − µ) 2 ] = N − 1 N σ 2 = (1 − 1 N )σ 2 ▶ The unbiased estimate of sample variance should be: S ′ 2 = 1 N − 1 X N i=1 (Xi − X) 2 15 / 88
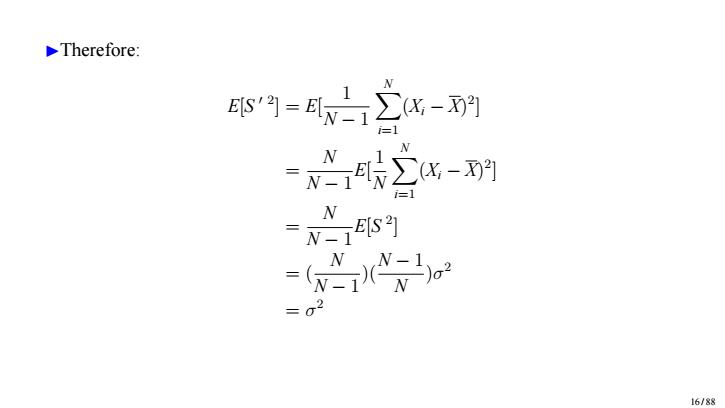
Therefore: 邱内=4w∑x-9 1 "∑x-明 E(S] N-11 16/88
▶Therefore: E [ S ′ 2 ] = E [ 1 N − 1 XNi=1 (Xi − X) 2 ] = N N − 1 E [ 1N XNi=1 (Xi − X) 2 ] = N N − 1 E [ S 2 ] = ( N N − 1 )( N − 1 N ) σ 2 = σ 2 16 / 88

Outline (Level 2) 2 Maximum Likelihood Estimation Example 1:Normal Distribution:unknown mean u and variance o2 Unbiased biased estimates ofu&o2 What is the global optimum of Gauss distribution ML? Exponential famil小y Example 2:Normal Distribution:known covariance matrix and unknown mean u 17/88
Outline (Level 2) 2 Maximum Likelihood Estimation Example 1: Normal Distribution: unknown mean µ and variance σ 2 Unbiased & biased estimates of µ & σ 2 What is the global optimum of Gauss distribution ML? Exponential family Example 2: Normal Distribution: known covariance matrix Σ and unknown mean µ 17 / 88

2.3.What is the global optimum of Gauss distribution ML? According to the least square method,we know that the following function has a minimum value at x. 品∑-驴≤∑-明=∑ For any o2,we have: (2no2npze Therefore,the x is the global optimal estimate of u. Is the a2 the best global solution? 18/88
2.3. What is the global optimum of Gauss distribution ML? ▶ According to the least square method, we know that the following function has a minimum value at x. 1 n Xn i=1 (xi − x) 2 ≤ 1 n Xn i=1 (xi − µ) 2 , x = 1 n Xn i=1 xi . ▶ For any σ 2 , we have: 1 (2πσ2 ) n/2 e −(1/2) ∑n i=1 (xi−x) 2/σ 2 ≥ 1 (2πσ2 ) n/2 e −(1/2) ∑n i=1 (xi−µ) 2/σ 2 ▶ Therefore, the x is the global optimal estimate of µ. ▶ Is the σ 2 the best global solution? 18 / 88

calculate the 2nd order derivative w.r.t.o2: aGplh,)=a-x- 02 i=1 Plugging the Ist order derivative stationary results w.r.t.u and o2: 应=无产=∑x-那 i-1 have: hu-京-4-=京-时= 02 264 The 2nd order derivative of Maximum likelihood function at point a2 is negative,therefore,it has maximum. 19/88
▶ calculate the 2nd order derivative w.r.t. σ 2 : ∂ 2 ∂(σ 2 ) 2 ln L(µ, σ2 |x) = n 2σ 4 − 1 σ 6 Xn i=1 (xi − µ) 2 ▶ Plugging the 1st order derivative stationary results w.r.t. µ and σ 2 : µˆ = x, σˆ 2 = 1 n Xn i=1 (xi − x) 2 have: ∂ 2 ∂(σ 2 ) 2 ln L(µ, σ2 |x) = n 2σ 4 − 1 σ 6 Xn i=1 (xi − µ) 2 = n 2ˆσ 4 − 1 σˆ 6 nσˆ 2 = − n 2ˆσ 4 ▶ The 2nd order derivative of Maximum likelihood function at point σˆ 2 is negative, therefore, it has maximum. 19 / 88