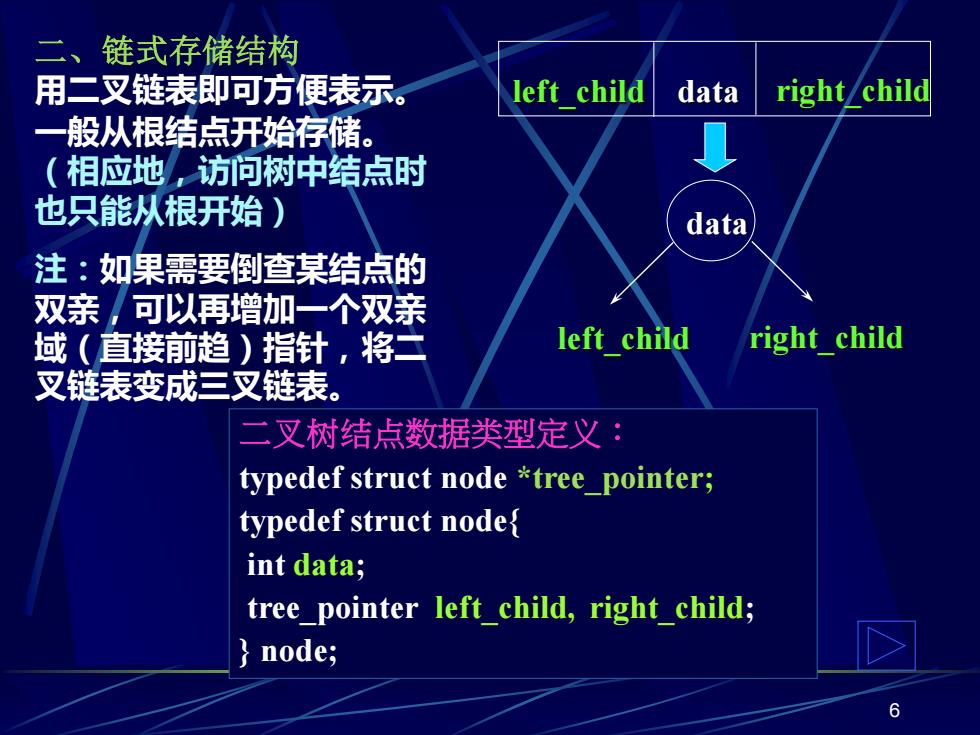
二、链式存储结构 用二叉链表即可方便表示。 left child data right/child 一般从根结点开始存储。 (相应地,访问树中结点时 也只能从根开始) data 注:如果需要倒查某结点的 双亲,可以再增加一个双亲 域(直接前趋)指针,将二 left child right child 叉链表变成三叉链表。 二叉树结点数据类型定义: typedef struct node *tree pointer; typedef struct node{ int data; tree pointer left child,right child; node; 6
6 二、链式存储结构 用二叉链表即可方便表示。 left_child data right_child data left_child right_child 二叉树结点数据类型定义: typedef struct node *tree_pointer; typedef struct node{ int data; tree_pointer left_child, right_child; } node; 一般从根结点开始存储。 (相应地,访问树中结点时 也只能从根开始) 注:如果需要倒查某结点的 双亲,可以再增加一个双亲 域(直接前趋)指针,将二 叉链表变成三叉链表

二叉树链式存储举例: B D EA 优点:①不浪费空间;②插入、删除方便
7 二叉树链式存储举例: A B E C D A ^ B ^ D C ^ ^ ^ E ^ 优点:①不浪费空间;②插入、删除方便

6.3遍历二叉树和线索二叉树 6.3.1遍历二叉树1 Traversing Binary Tree 遍历定义— 指按某条搜索路线遍访每个结点且不重复 (又称周游) 遍历用途 它是树结构插入、删除、修改、 查找和排序运 算的前提,是二叉树一切运算的基础和核心。 遍历方法 对每个结点的查看通常都是“先左后右
8 6.3 遍历二叉树和线索二叉树 6.3.1 遍历二叉树 遍历定义—— 遍历用途—— 遍历方法—— 指按某条搜索路线遍访每个结点且不重复 (又称周游)。 它是树结构插入、删除、修改、查找和排序运 算的前提,是二叉树一切运算的基础和核心。 对每个结点的查看通常都是“先左后右” 。 Traversing Binary Tree

遍历规则 二叉树由抽想 医子树佑子树构成,定义为D、L、R DL、 R的组合定义了六种可能的遍历方案 LDR,LRD,DLR,DRL RDD, RLD 若限定先左后右,则有三种实现方案: DLR LDR LRD 先序遍历 中序遍历 后序遍历 注:(“先、中、房”的意思是指访问的结点D是先于子树出 现还是后于子树出现。 以根结点为参照系 9
9 遍历规则——— ❖ 二叉树由根、左子树、右子树构成,定义为D、 L、R 以根结点为参照系 注:“先、中、后”的意思是指访问的结点D是先于子树出 现还是后于子树出现。 ❖ D、 L、R的组合定义了六种可能的遍历方案: LDR, LRD, DLR, DRL, RDL, RLD ❖ 若限定先左后右,则有三种实现方案: DLR LDR LRD 先序遍历 中序遍历 后序遍历
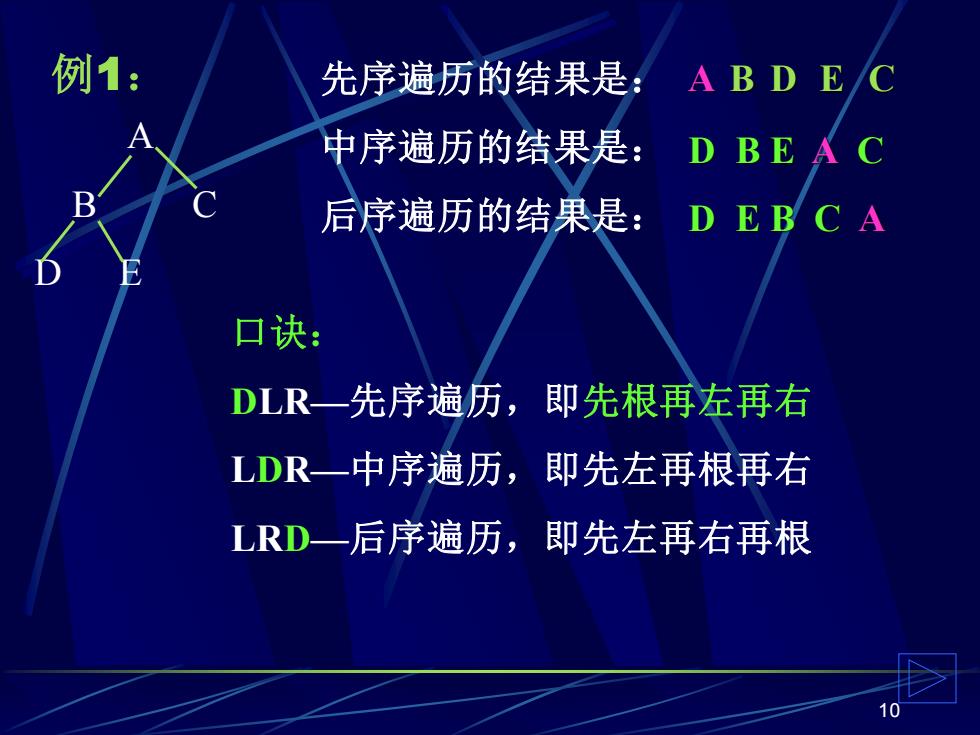
例1: 先序遍历的结果是: ABD EC 中序遍历的结果是:】 D BEAC 后序遍历的结果是:DEBCA 口诀: DLR一先序遍历,即先根再左再右 LDR一中序遍历,即先左再根再右 LRD一后序遍历,即先左再右再根 10
10 例1: 先序遍历的结果是: 中序遍历的结果是: 后序遍历的结果是: A B C D E D B E A C D E B C A 口诀: DLR—先序遍历,即先根再左再右 LDR—中序遍历,即先左再根再右 LRD—后序遍历,即先左再右再根 A B D E C