
信道容量的来历 ③这个公式跟逐个符号的功率约束有什么关系? c=wio(1+) 带限AWGN信道容量 Shannon,1948 之关系不明显。 但跟该公式的前身关系密切: c=2og21+3) 离散AWGN信道容量 量纲:bits/symbol ?这个公式又是怎么来的? ③从这个公式怎么得到带限AWGN信道容量的? 2020年秋季 11/62 无线互联网
信道容量的来历 2020年秋季 11 / 62 无线互联网 这个公式跟逐个符号的功率约束有什么关系? � = � ���� � + � ��� 带限AWGN信道容量 Shannon,1948 关系不明显。 但跟该公式的前身关系密切: � = � � ���� � + � �� 离散AWGN信道容量 量纲:bits/symbol 这个公式又是怎么来的? 从这个公式怎么得到带限AWGN信道容量的?

离散AWGN信道(1/5) 离散AWGN信道模型:Y=X+Z ①信道输入X和输出Y都是n个符号构成的序列:消息 ◆n次使用信道(《数字通信》第5版,Proakis) ◆n维扩展信道(《通信系统原理》,Proakis) 四例如:符号集为{0,1},n=3,消息集合为{000,,111} 今信道输入的符号功率约束为: x好≤P n Z为方差为σ2的零均值高斯随机变量。 2020年秋季 12/62 无线互联网
离散AWGN信道(1/5) 2020年秋季 12 / 62 无线互联网 离散AWGN信道模型:� = � + � 信道输入�和输出�都是�个符号构成的序列:消息 �次使用信道(《数字通信》第5版,Proakis) �维扩展信道(《通信系统原理》,Proakis) 例如:符号集为{0, 1},n=3,消息集合为{000,…,111} 信道输入的符号功率约束为: � �O �+� � �� � ≤ � �为方差为��的零均值高斯随机变量

离散AWGN信道(2/5) 当n足够大时,由大数定理可知: n n y1-xl2≤a2 n i=1 i=1 1y-x|2≤na2 ly12≤n(P+o2) 随着n的增加,当输 随着n的增加,输出y 入为x时,输出y处于 处于以Vn(P+o2)为 以x为中心,以Vno2 半径的m维球内的概 为半径的n维球内的 率趋近于1。 概率趋近于1。 2020年秋季 13/62 无线互联网
离散AWGN信道(2/5) 2020年秋季 13 / 62 无线互联网 当�足够大时,由大数定理可知: � �O �+� � �� − �� � ≤ �� � �O �+� � �� � ≤ � + �� � − � � ≤ ��� � � ≤ � � + �� 随着�的增加,当输 入为�时,输出�处于 以�为中心,以 ��� 为半径的�维球内的 概率趋近于1。 随着�的增加,输出� 处于以 � � + �� 为 半径的�维球内的概 率趋近于1
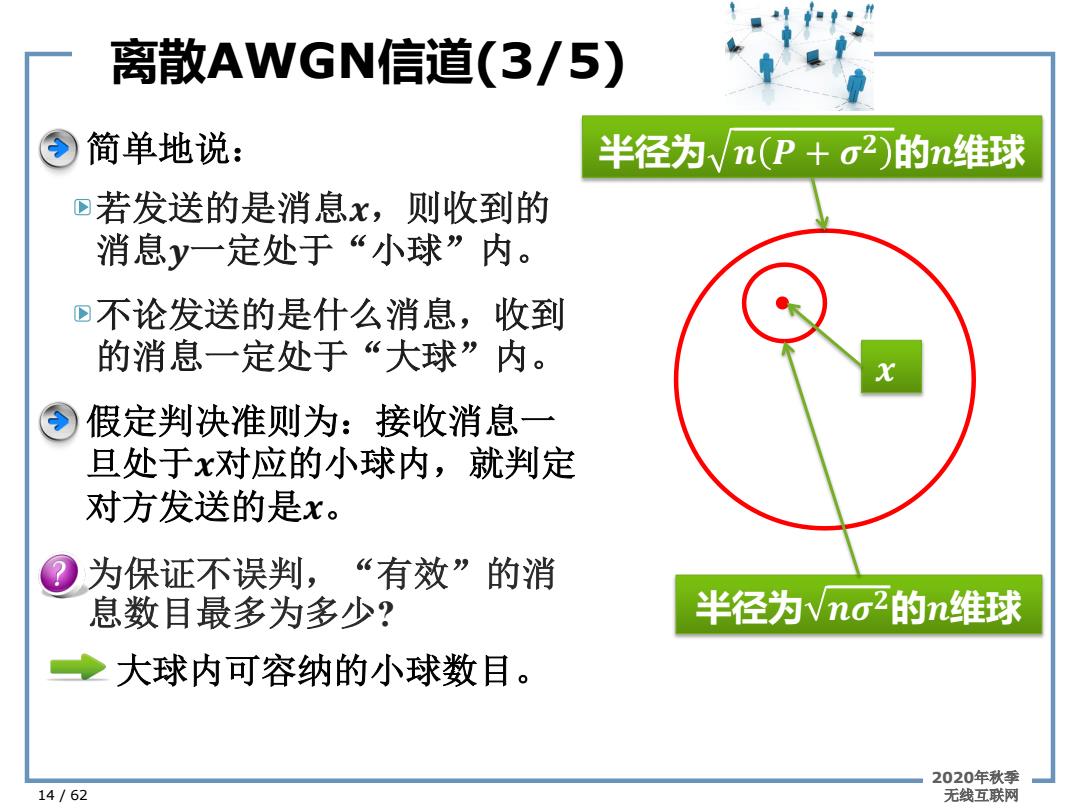
离散ANGN信道(3/5) 简单地说: 半径为√n(P+σ2)的n维球 四若发送的是消息x,则收到的 消息y一定处于“小球”内。 四不论发送的是什么消息,收到 的消息一定处于“大球”内。 假定判决准则为:接收消息一 旦处于x对应的小球内,就判定 对方发送的是x。 ?为保证不误判,“有效”的消 息数目最多为多少? 半径为Vnc2的n维球 ◆大球内可容纳的小球数目。 2020年秋季 14/62 无线互联网
离散AWGN信道(3/5) 2020年秋季 14 / 62 无线互联网 半径为 � � + �� 的�维球 半径为 ���的�维球 � 简单地说: 若发送的是消息�,则收到的 消息�一定处于“小球”内。 不论发送的是什么消息,收到 的消息一定处于“大球”内。 假定判决准则为:接收消息一 旦处于�对应的小球内,就判定 对方发送的是�。 为保证不误判, “有效”的消 息数目最多为多少? 大球内可容纳的小球数目

离散AWGN信道(4/5) 维球体积?◆2R(线段长度) 二维球体积?◆ πR2(圆面积) ?三维球体积? 言πR3(球体积 n维球体积? KnRn 保证可靠通信的消息数目最多为: 2 M= -a ①M的含义:AWGN信道能容纳的消息种类最多就是它了。 2020年秋季 15/62 无线互联网
离散AWGN信道(4/5) 2020年秋季 15 / 62 无线互联网 一维球体积? ��(线段长度) 二维球体积? ���(圆面积) 三维球体积? � ����(球体积) �维球体积? ���� 保证可靠通信的消息数目最多为: � = �� � � + �� � �� ��� � = � + � �� � � �的含义:AWGN信道能容纳的消息种类最多就是它了