
信息检索与数据挖掘 2019/4/22 12 二元线性分类器的形式化定义 函数间隔 .w:decision hyperplane normal vector w:决策超平面的法向量,下图中为a .x,:data point i b:决策超平面的截距 y:class of data point i(+1 or-1) arx≥-b ax≤-b .Classifier is:f(x)=sign(wx;+b) ·函数间隔 Functional margin of x,is: yi(wx;+b) Functional margin of dataset is twice the minimum functional margin for any point The factor of 2 comes from measuring the whole width of the margin dist(C,D)=inf{u-vll2u∈C,v∈D}
信息检索与数据挖掘 2019/4/22 12 二元线性分类器的形式化定义 函数间隔 • w: decision hyperplane normal vector • xi : data point i • yi : class of data point i (+1 or -1) • Classifier is: f(xi ) = sign(wTxi + b) • 函数间隔 • Functional margin of xi is: yi (wTxi + b) • Functional margin of dataset is twice the minimum functional margin for any point • The factor of 2 comes from measuring the whole width of the margin w: 决策超平面的法向量,下图中为a b: 决策超平面的截距 -b -b

信息检索与数据挖掘 2019/4/22 13 Geometric Margin 分类器的几何间隔:中间空白带的最大宽度, 几何间隔 该空白带可以用于将两类支持向量分开 wx+b Distance from example to the separator is r=y 点x到决策平面的距离r: w x向量在法向量w上的投影 Examples closest to the hyperplane are support vectors. Margin p of the separator is the width of separation between support vectors of classes. Derivation of finding r: Dotted line x'-x is perpendicular to decision boundary so parallel to w. Unit vector is w/w,so line is rw/|w. x'=x-yrw/wl. x'satisfies wx'+b 0. SowT(x-ywl小w)+b=0 Recall that |w sqrt(wTw) So,solving for r gives: r y(wTx b)/wl yj:class of data point i(+1 or-1)
信息检索与数据挖掘 2019/4/22 13 Geometric Margin 几何间隔 • Distance from example to the separator is • Examples closest to the hyperplane are support vectors. • Margin ρ of the separator is the width of separation between support vectors of classes. w w x b r y T r ρ x x′ w Derivation of finding r: Dotted line x’−x is perpendicular to decision boundary so parallel to w. Unit vector is w/|w|, so line is rw/|w|. x’ = x – yrw/|w|. x’ satisfies wTx’+b = 0. So wT(x –yrw/|w|) + b = 0 Recall that |w| = sqrt(wTw). So, solving for r gives: r = y(wTx + b)/|w| 分类器的几何间隔: 中间空白带的最大宽度, 该空白带可以用于将两类支持向量分开 点x到决策平面的距离r: x向量在法向量w上的投影 yi : class of data point i (+1 or -1)
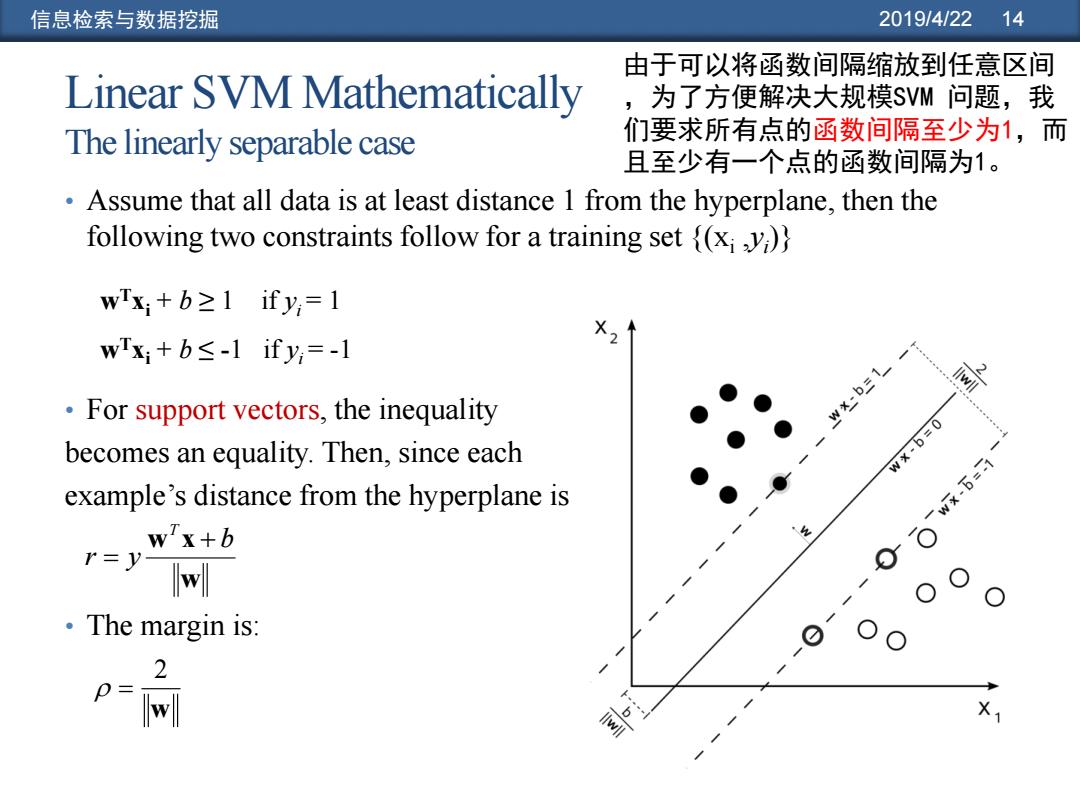
信息检索与数据挖掘 2019/4/22 14 由于可以将函数间隔缩放到任意区间 Linear SVM Mathematically ,为了方便解决大规模SVM问题,我 The linearly separable case 们要求所有点的函数间隔至少为1,而 且至少有一个点的函数间隔为1。 Assume that all data is at least distance 1 from the hyperplane,then the following two constraints follow for a training set {(xi)) wTx+b≥1ify,=1 wx+b≤-1ify,=-1 For support vectors,the inequality w×b三1 becomes an equality.Then,since each w×-b=0 example's distance from the hyperplane is wx-= w7x+b r=y w ·The margin is: 2 w X1
信息检索与数据挖掘 2019/4/22 14 Linear SVM Mathematically The linearly separable case • Assume that all data is at least distance 1 from the hyperplane, then the following two constraints follow for a training set {(xi ,yi )} • For support vectors, the inequality becomes an equality. Then, since each example’s distance from the hyperplane is • The margin is: wTxi + b ≥ 1 if yi = 1 wTxi + b ≤ -1 if yi = -1 w 2 w w x b r y T 由于可以将函数间隔缩放到任意区间 ,为了方便解决大规模SVM 问题,我 们要求所有点的函数间隔至少为1,而 且至少有一个点的函数间隔为1

信息检索与数据挖掘 2013e0225.15 Linear Support Vector Machine(SVM) wTxa b=1 。Hyperplane wTx+b=0 wTx+b三-1 Extra scale constraint: min=l,…nlwX+bl=1 This implies: w(Xa-Xp)=2 p llxa-xpll2 2/1lwll2 WTx+b=0 我们的目标是最大化分类间隔p
信息检索与数据挖掘 2019/4/22 15 Linear Support Vector Machine (SVM) • Hyperplane wT x + b = 0 • Extra scale constraint: mini=1,…,n |wTxi + b| = 1 • This implies: wT(xa–xb ) = 2 ρ = ||xa–xb ||2 = 2/||w||2 wT x + b = 0 wTxa + b = 1 wTxb + b = -1 ρ Sec. 15.1 我们的目标是最大化分类间隔ρ

信息检索与数据挖掘 2019/4/22 16 Linear SVMs Mathematically (cont.) Then we can formulate the quadratic optimization problem: Find w and b such that P= 网 is maximized;and for all {, wx+b≥1ify=1;wx+b≤-1ify,=-1 A better formulation (min lwll max 1/lwl ) 市=√市 Find w and b such that (w)=%wTw is minimized; and for all {(xi):y (wxi+b)>1 上述问题实际上是在线性约束条件下的二次函数优化问题。该问题是数学中 的基本问题之一,存在很多解决算法(比如,有一些二次规划库)
信息检索与数据挖掘 2019/4/22 16 Linear SVMs Mathematically (cont.) • Then we can formulate the quadratic optimization problem: • A better formulation (min ||w|| = max 1/ ||w|| ): Find w and b such that is maximized; and for all {(xi , yi )} wTxi + b ≥ 1 if yi=1; wTxi + b ≤ -1 if yi = -1 w 2 Find w and b such that Φ(w) =½ wTw is minimized; and for all {(xi ,yi )}: yi (wTxi + b) ≥ 1 上述问题实际上是在线性约束条件下的二次函数优化问题。该问题是数学中 的基本问题之一,存在很多解决算法 (比如,有一些二次规划库)