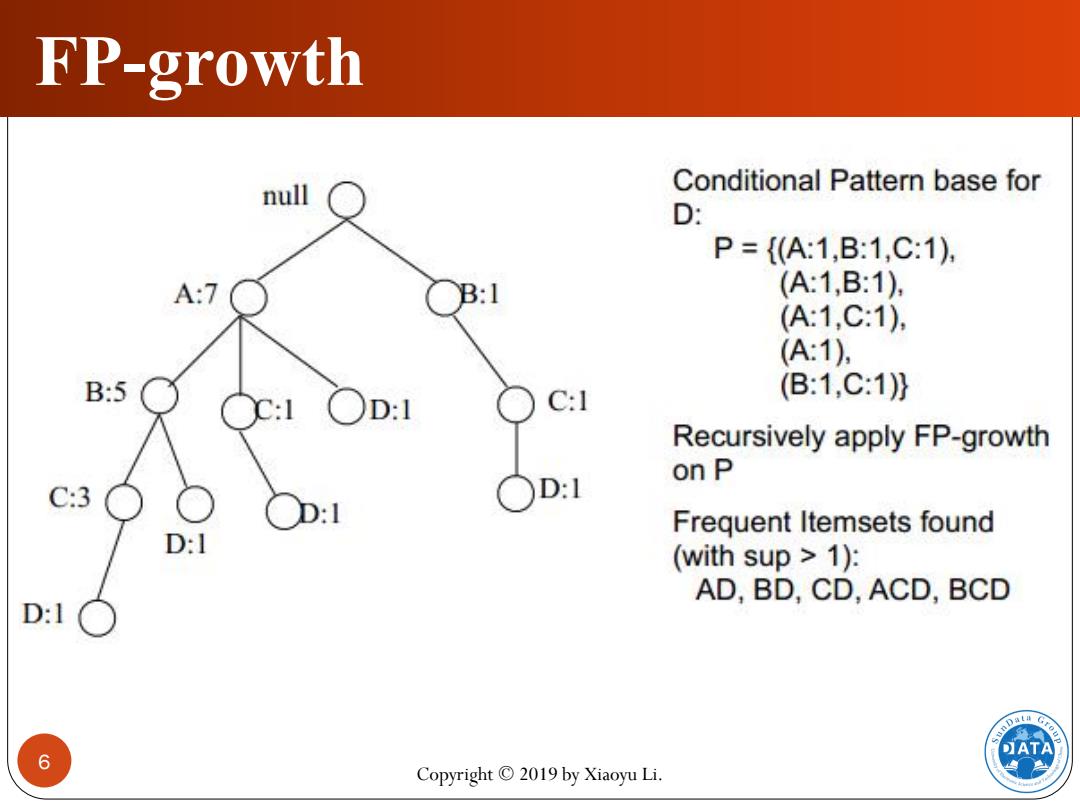
FP-growth null Conditional Pattern base for D: P={A:1,B:1,C:1) A:7 B:1 (A1,B:1) (A:1,C:1) (A:1), B:5 C:I (B1,C:1)} D:1 Recursively apply FP-growth C:3 ○Dl on P D:1 Frequent Itemsets found D:I (with sup>1): AD,BD,CD,ACD,BCD D:1 ATA 6 Copyright 2019 by Xiaoyu Li
6 Copyright © 2019 by Xiaoyu Li. FP-growth

Rule Generation Given a frequent itemset L,find all non-empty subsets f CL such that f-L-f satisfies the minimum confidence requirement If [A,B,C,D}is a frequent itemset,candidate rules: ABC→D, ABD→C, ACD→B, BCD→A, A→BCD, B→ACD, C→ABD, D→ABC AB→CD AC→BD, AD→BC BC→AD, BD→AC CD→AB, llf L =k,then there are 2k-2 candidate association rules(ignoring L→☑and☑→L) ATA Copyright 2019 by Xiaoyu Li
7 Copyright © 2019 by Xiaoyu Li. Rule Generation

Rule generation How to efficiently generate rules from frequent itemsets? In general,confidence does not have an anti- monotone property c(ABC→D)can be larger or smaller than c(AB→D) But confidence of rules generated from the same itemset has an anti-monotone property -e.g.,L=(A,B,C,D): c(ABC→D)2c(AB→CD)≥c(A→BCD) Confidence is anti-monotone w.r.t.number of items on the RHS of the rule ATA 8 Copyright 2019 by Xiaoyu Li
8 Copyright © 2019 by Xiaoyu Li. Rule Generation
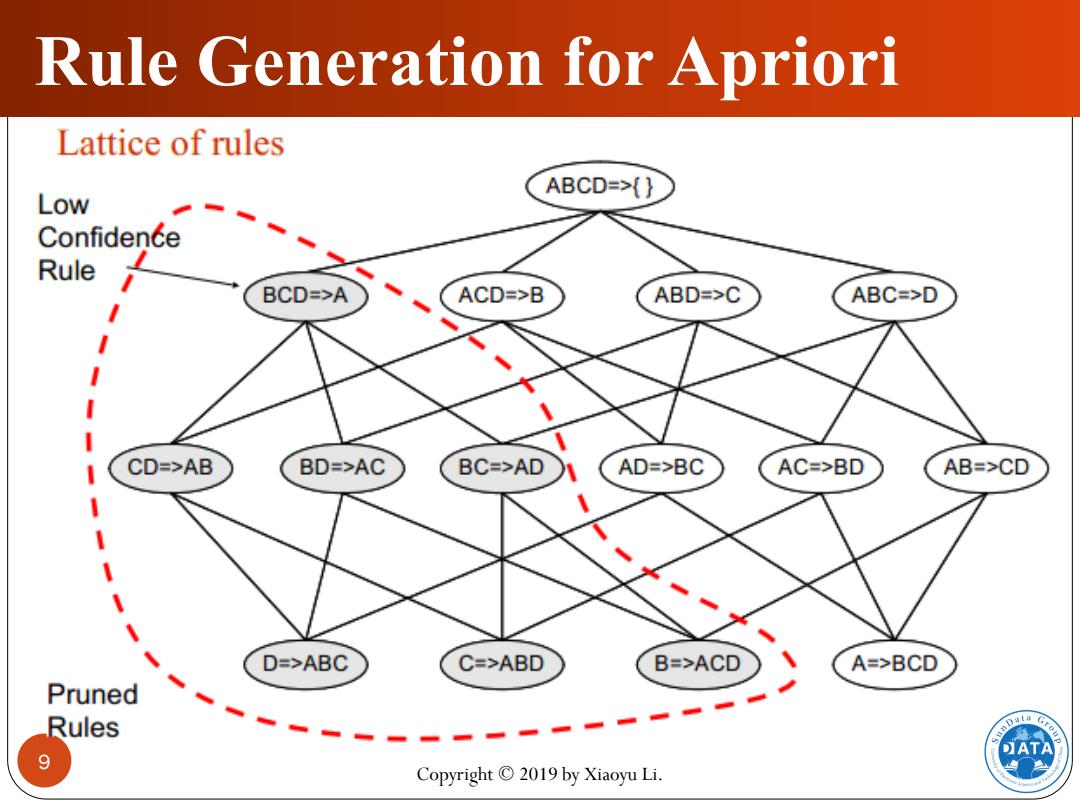
Rule Generation for Apriori Lattice of rules ABCD=>(} Low Confidence Rule BCD=>A ACD=>B ABD=>C ABC=>D CD=>AB BD=>AC BC=>AD AD=>BC AC=>BD AB=>CD D=>ABC C=>ABD B=>ACD A=>BCD Pruned Rules ATA 9 Copyright 2019 by Xiaoyu Li
9 Copyright © 2019 by Xiaoyu Li. Rule Generation for Apriori

Rule Generation for Apriori Candidate rule is generated by merging two rules that share the same prefix in the rule consequent CD=>AB BD=>AC join(CD=>AB,BD=>AC) would produce the candidate rule D =ABC Prune rule D=>ABC if its D=>ABC subset AD=>BC does not have high confidence DATA 10 Copyright 2019 by Xiaoyu Li
10 Copyright © 2019 by Xiaoyu Li. Rule Generation for Apriori