
对称面(P)与反映操作对称面是一个假想平面,它将图形平分成互为镜像的两个部分。对称面以P表示。有一个对称面记作P,有多个对称面时,数字写在P的前面。一个晶体不一定具有对称面,也可以不止一个对称面,但最多不超过9个。P切面是矩形体的对称面;Q切面不是矩形体的对称面该切面不是矩该切面是形体的对称面对称面
一、对称面(P)与反映操作 • 对称面是一个假想平面,它将图形平分成互为镜像的两个 部分。对称面以P表示。有一个对称面记作P,有多个对称 面时,数字写在P的前面。一个晶体不一定具有对称面, 也可以不止一个对称面,但最多不超过9个。 P切面是 矩形体的 对称面; Q切面不 是矩形体 的对称面 该切面是 对称面 该切面 不是矩 形体的 对称面

对称面在晶体上的出露位置垂直并平分晶面垂直晶棱并通过晶棱中点包含晶棱。立方体的9个对称面·注意:1)寻找对称面时要尽量避免转动模型,以免造成重复;2)两部分上对应点的连线是否与对称面垂直等距
对称面在晶体上的出露位置: • 垂直并平分晶面 • 垂直晶棱并通过晶棱中点 • 包含晶棱。 • 注意: 1)寻找对称面时要尽量避免转动模型,以免造成重 复; 2)两部分上对应点的连线是否与对称面垂直等距。 立方体的9个对称面

对称轴(Ln)与旋转操作对称轴是通过晶体中心的一根假想直线:晶体绕该直线旋转一定角度后,使晶体相同的部分出现重复。晶体旋转一周重复的次数称为轴次n。重复一次所旋转的最小角度称基转角α。轴次与基转角的关系为n=360°/α。N横面横炭面横炭面横面对称轴类型习惯符号基准角图示符号对称轴类型习惯符号基准角图示符号LIL660°360°一次对称轴六次对称轴L2L4180°90°二次对称轴四次旋转反伸轴L3L6120°60°三次对称轴六次旋转对称轴L490°四次对称轴
二、对称轴(Ln)与旋转操作 • 对称轴是通过晶体中心的一根假想直线:晶体绕 该直线旋转一定角度后,使晶体相同的部分出现 重复。 • 晶体旋转一周重复的次数称为轴次n。 • 重复一次所旋转的最小角度称基转角α。轴次与 基转角的关系为n=360°/α。 对称轴类型 习惯符号 基准角 图示符号 对称轴类型 习惯符号 基准角 图示符号 一次对称轴 L 1 360° 六次对称轴 L 6 60° 二次对称轴 L 2 180° 四次旋转反伸轴 L i 4 90° 三次对称轴 L 3 120° 六次旋转对称轴 L i 6 60° 四次对称轴 L 4 90°

晶体对称定律:(格子构造的限制)晶体中没有五次对称轴和高于六次的对称轴。即晶体中可能出现的对称轴只能是L1、L2、L3、L4、L6,没有L5以及轴次高于L6的对称轴存在。为什么呢?1、直观形象的理解:垂直五次及高于六次的(c)对称轴的平面结构不能38构成面网,耳不能毫无间隙地铺满整个空间(d)(g)即不能成为晶体结构
• 晶体对称定律 :(格子构造的限制) • 晶体中没有五次对称轴和高于六次的对称轴。即 晶体中可能出现的对称轴只能是L 1 、L 2 、L 3 、L 4 、 L 6,没有L 5以及轴次高于L 6的对称轴存在。 为什么呢? 1、直观形象的理解: 垂直五次及高于六次的 对称轴的平面结构不能 构成面网,且不能毫无 间隙地铺满整个空间, 即不能成为晶体结构
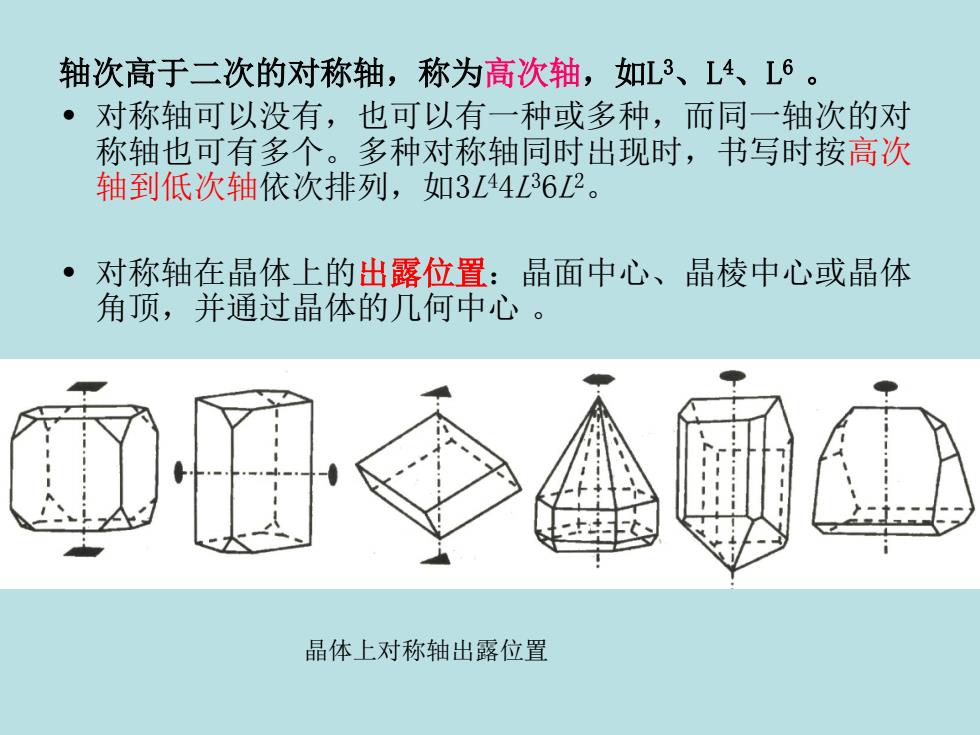
轴次高于二次的对称轴,称为高次轴,如L3、L4、L6。对称轴可以没有,也可以有一种或多种,而同一轴次的对称轴也可有多个。多种对称轴同时出现时,书写时按高次轴到低次轴依次排列,如3L44L36L2。对称轴在晶体上的出露位置:晶面中心、晶棱中心或晶体角顶,并通过晶体的几何中心。晶体上对称轴出露位置
轴次高于二次的对称轴,称为高次轴,如L 3 、L 4 、L 6 。 • 对称轴可以没有,也可以有一种或多种,而同一轴次的对 称轴也可有多个。多种对称轴同时出现时,书写时按高次 轴到低次轴依次排列,如3L 44L 36L 2 。 • 对称轴在晶体上的出露位置:晶面中心、晶棱中心或晶体 角顶,并通过晶体的几何中心 。 晶体上对称轴出露位置