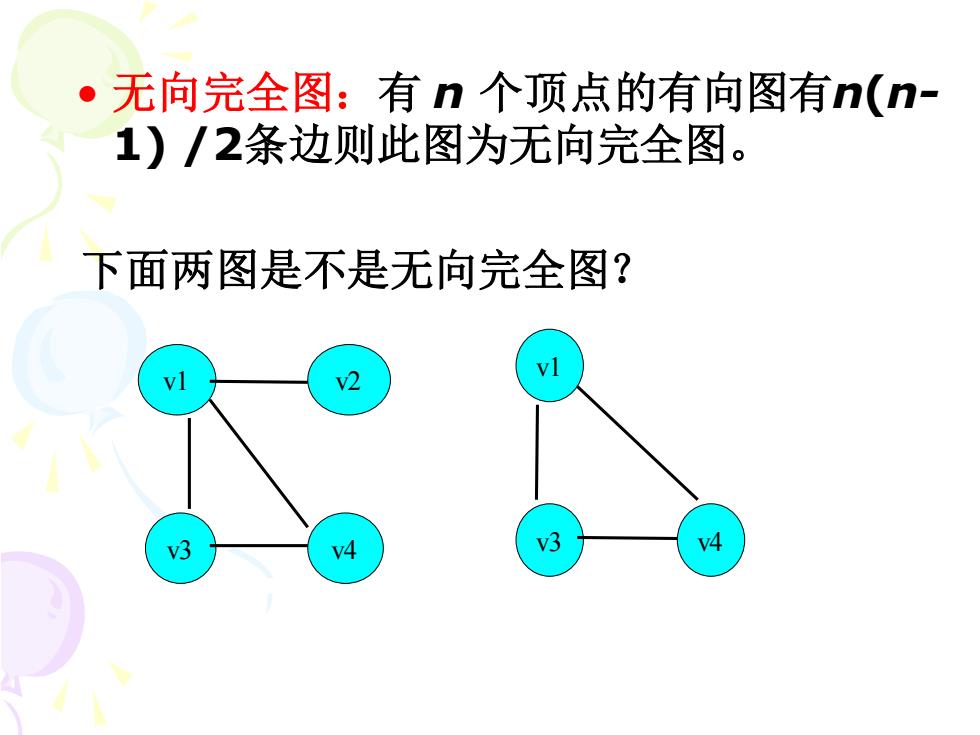
无向完全图:有n个顶点的有向图有n(n- 1)/2条边则此图为无向完全图。 下面两图是不是无向完全图? vl 2 3 v4 v3 4
• 无向完全图:有 n 个顶点的有向图有n(n- 1) /2条边则此图为无向完全图。 v1 v2 v3 v4 v1 v3 v4 下面两图是不是无向完全图?
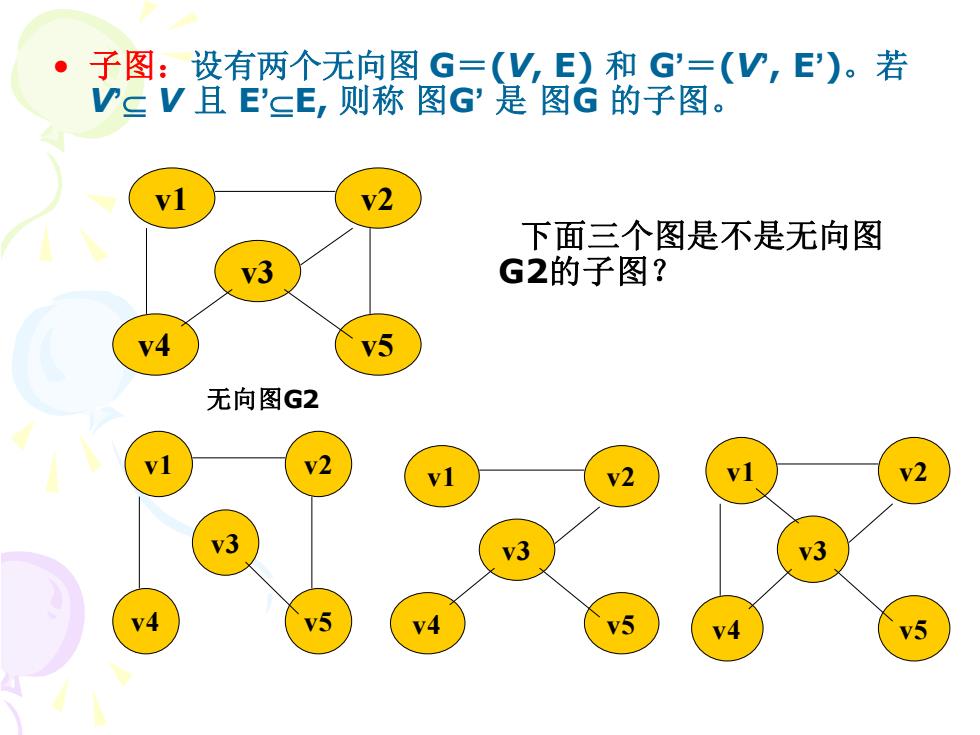
子图:设有两个无向图G=(V,E)和G=(V,E)。若 V三V且E'sE,则称图G?是图G的子图。 下面三个图是不是无向图 G2的子图? v4 v5 无向图G2 2 v2 v3 V4 v5
• 子图:设有两个无向图 G=(V, E) 和 G’=(V’, E’)。若 V’ V 且 E’E, 则称 图G’ 是 图G 的子图。 v4 v5 v3 v1 v2 无向图G2 v4 v5 v3 v1 v2 v4 v5 v3 v1 v2 v4 v5 v3 v1 v2 下面三个图是不是无向图 G2的子图?
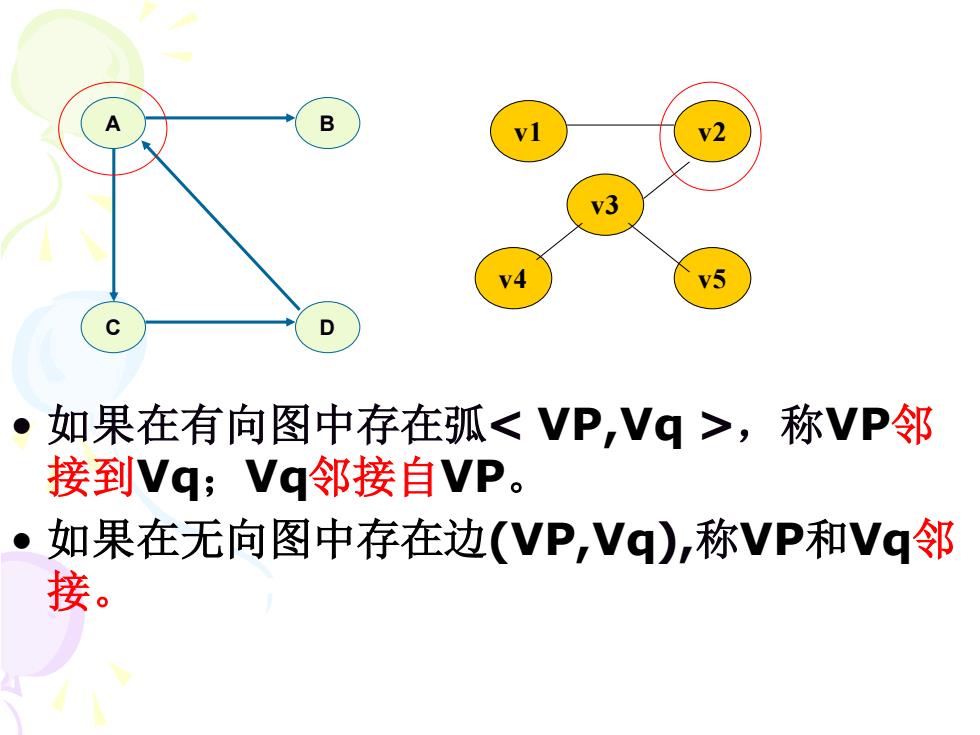
B vl v2 y3 5 C D ● 如果在有向图中存在弧<VP,Vq>,称VP邻 接到Vq;Vq邻接自VP。 如果在无向图中存在边(VP,Vq),称VP和Vq邻 接
• 如果在有向图中存在弧< VP,Vq >,称VP邻 接到Vq;Vq邻接自VP。 • 如果在无向图中存在边(VP,Vq),称VP和Vq邻 接。 A B C D v4 v5 v3 v1 v2
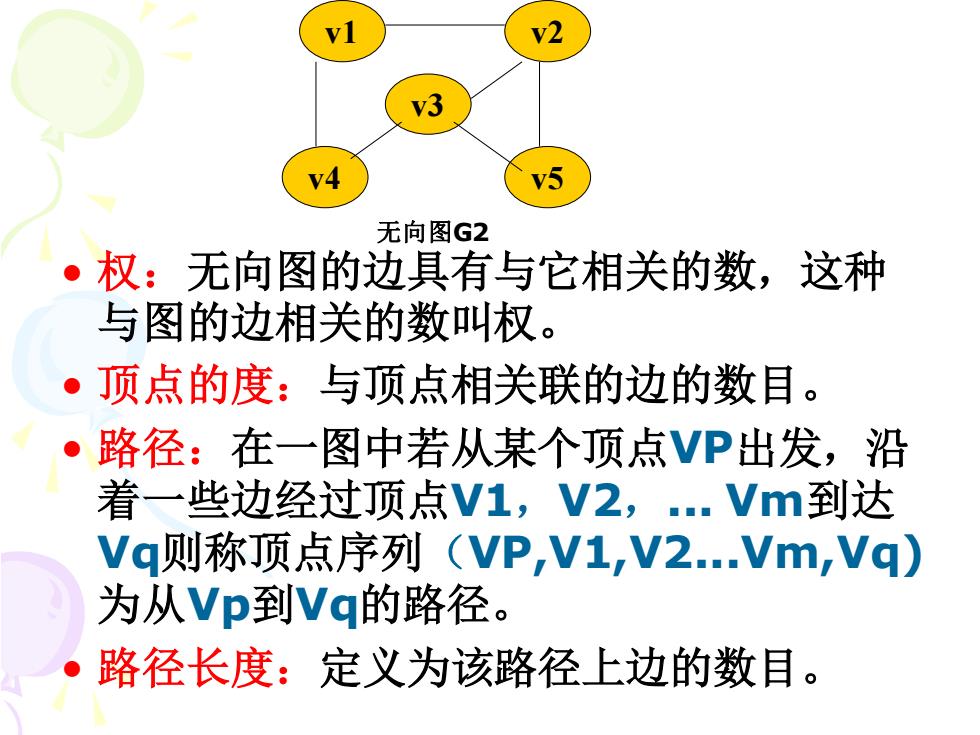
v5 无向图G2 权:无向图的边具有与它相关的数,这种 与图的边相关的数叫权。 顶点的度:与顶点相关联的边的数目。 路径:在一图中若从某个顶点VP出发,沿 着一些边经过顶点V1,V2,.Vm到达 Vq则称顶点序列(VP,V1,V2.Vm,Vq) 为从Vp到Vq的路径。 路径长度:定义为该路径上边的数目
• 权:无向图的边具有与它相关的数,这种 与图的边相关的数叫权。 • 顶点的度:与顶点相关联的边的数目。 • 路径:在一图中若从某个顶点VP出发,沿 着一些边经过顶点V1,V2,. Vm到达 Vq则称顶点序列(VP,V1,V2.Vm,Vq) 为从Vp到Vq的路径。 • 路径长度:定义为该路径上边的数目。 v4 v5 v3 v1 v2 无向图G2
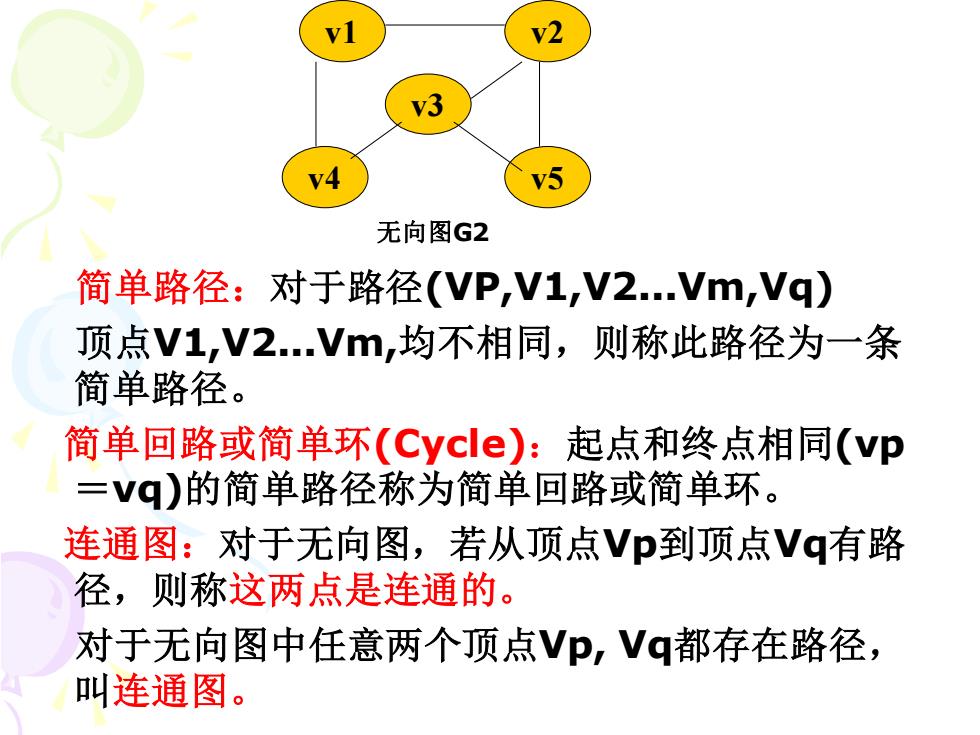
3 无向图G2 简单路径:对于路径(VP,V1,V2.Vm,Vq) 项点V1,V2.Vm,均不相同,则称此路径为一条 简单路径。 简单回路或简单环(Cycle):起点和终点相同(vp =Vq)的简单路径称为简单回路或简单环。 连通图:对于无向图,若从顶点Vp到顶点Vq有路 径,则称这两点是连通的。 对于无向图中任意两个顶点Vp,Vq都存在路径, 叫连通图
简单路径:对于路径(VP,V1,V2.Vm,Vq) 顶点V1,V2.Vm,均不相同,则称此路径为一条 简单路径。 简单回路或简单环(Cycle):起点和终点相同(vp =vq)的简单路径称为简单回路或简单环。 连通图:对于无向图,若从顶点Vp到顶点Vq有路 径,则称这两点是连通的。 对于无向图中任意两个顶点Vp, Vq都存在路径, 叫连通图。 v4 v5 v3 v1 v2 无向图G2