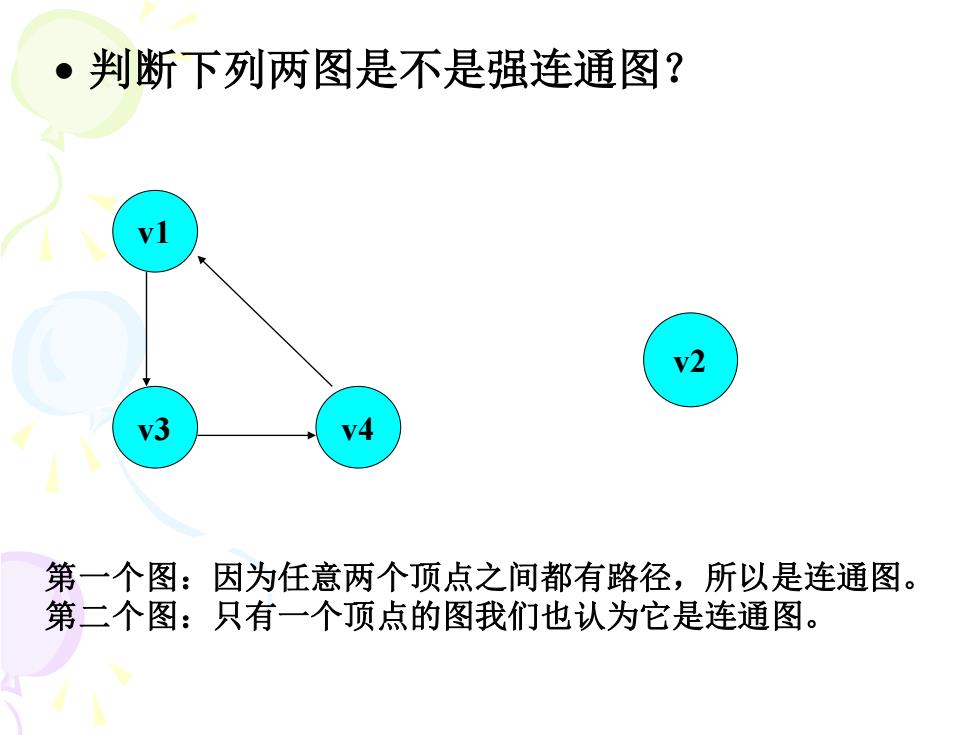
判断下列两图是不是强连通图? vl v2 第一个图:因为任意两个顶点之间都有路径,所以是连通图。 第二个图:只有一个顶点的图我们也认为它是连通图
• 判断下列两图是不是强连通图? v1 v3 v4 v2 第一个图:因为任意两个顶点之间都有路径,所以是连通图。 第二个图:只有一个顶点的图我们也认为它是连通图

强连通分量:有向图中的极大连通子图称为 强连通分量。 (复杂一点的有向图的强连通分量找起来很 麻烦,必须编程序让计算机找。) ● 注意三点问题: 。首先,它必须是有向图的子图。 。其次,它必须是连通的。 再次,它必须是极大的(看有没有包含它的 更大的子图也是连通的?如果有,它就不是 极大的;没有,它就是极大的)
• 强连通分量:有向图中的极大连通子图称为 强连通分量。 • (复杂一点的有向图的强连通分量找起来很 麻烦,必须编程序让计算机找。) • 注意三点问题: • 首先,它必须是有向图的子图。 • 其次,它必须是连通的。 • 再次,它必须是极大的(看有没有包含它的 更大的子图也是连通的?如果有,它就不是 极大的;没有,它就是极大的)
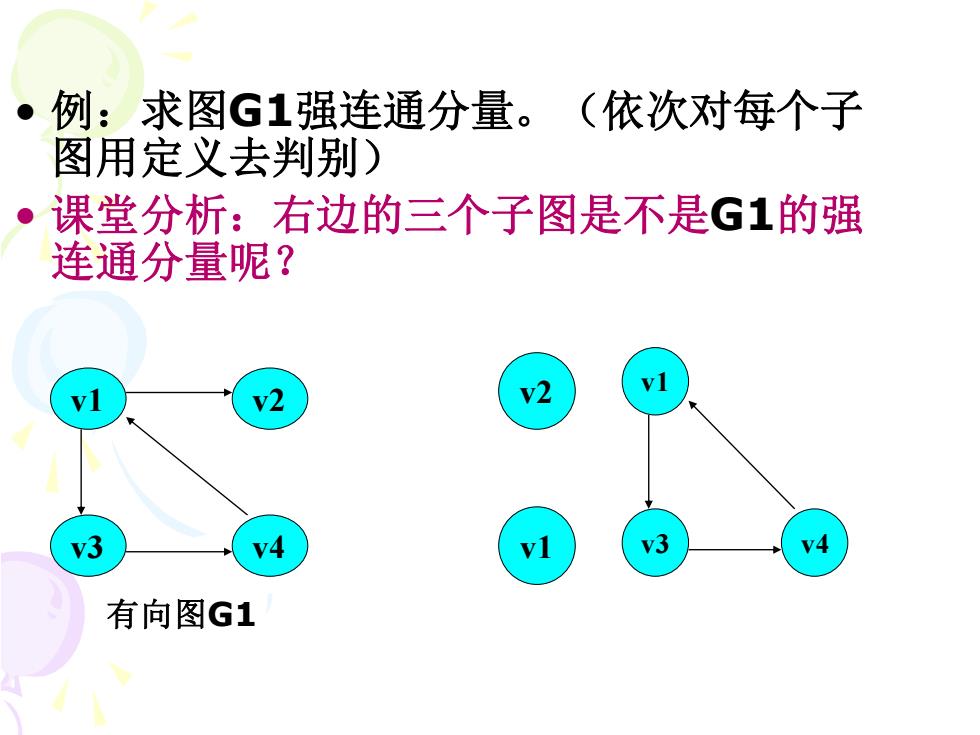
● 例:求图G1强连通分量。(依次对每个子 图用定义去判别) ·课堂分析:右边的三个子图是不是G1的强 连通分量呢? v2 v3 V4 V3 有向图G1
v1 v2 v3 v4 有向图G1 • 例:求图G1强连通分量。(依次对每个子 图用定义去判别) • 课堂分析:右边的三个子图是不是G1的强 连通分量呢? v2 v1 v1 v3 v4

v2 v2 y3 有向图G1 是有向图G1的子图,是连通的。但它是不 是极大的呢?能不能找到包含它的更大的子 图也是连通的? 找不到包含它的更大的子图也是连通的, 所以它就是极大的。所以它是强连通分量
• 是有向图G1的子图,是连通的。但它是不 是极大的呢?能不能找到包含它的更大的子 图也是连通的? • 找不到包含它的更大的子图也是连通的, 所以它就是极大的。所以它是强连通分量 。 v1 v2 v3 v4 有向图G1 v2
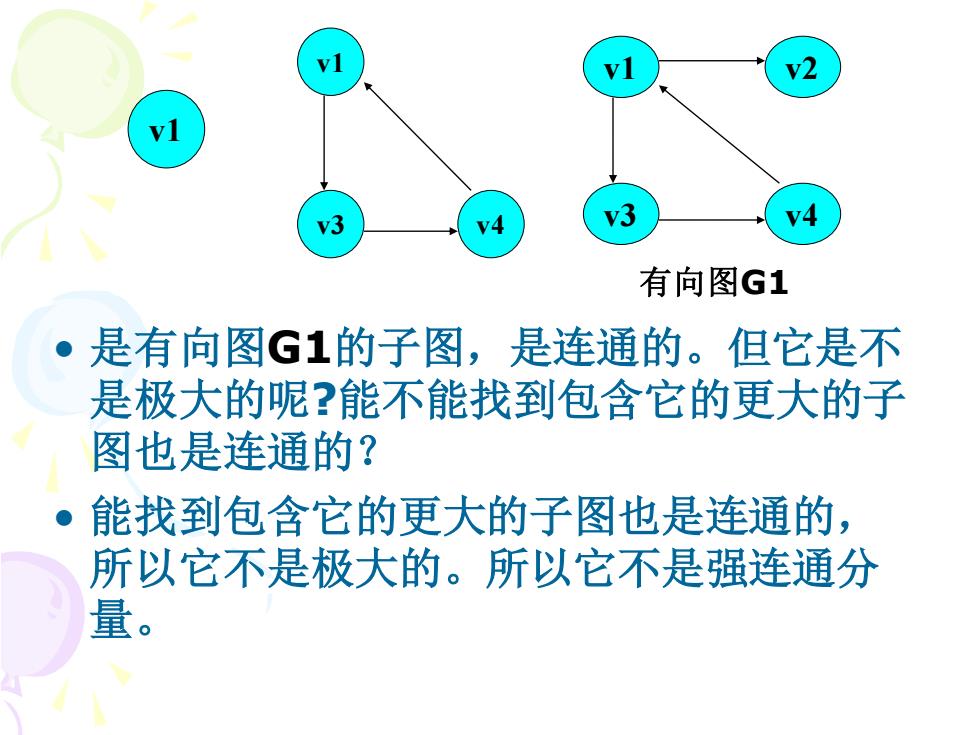
v2 v3 有向图G1 是有向图G1的子图,是连通的。但它是不 是极大的呢?能不能找到包含它的更大的子 图也是连通的? 能找到包含它的更大的子图也是连通的, 所以它不是极大的。所以它不是强连通分 量
• 是有向图G1的子图,是连通的。但它是不 是极大的呢?能不能找到包含它的更大的子 图也是连通的? • 能找到包含它的更大的子图也是连通的, 所以它不是极大的。所以它不是强连通分 量。 v1 v2 v3 v4 有向图G1 v1 v1 v3 v4