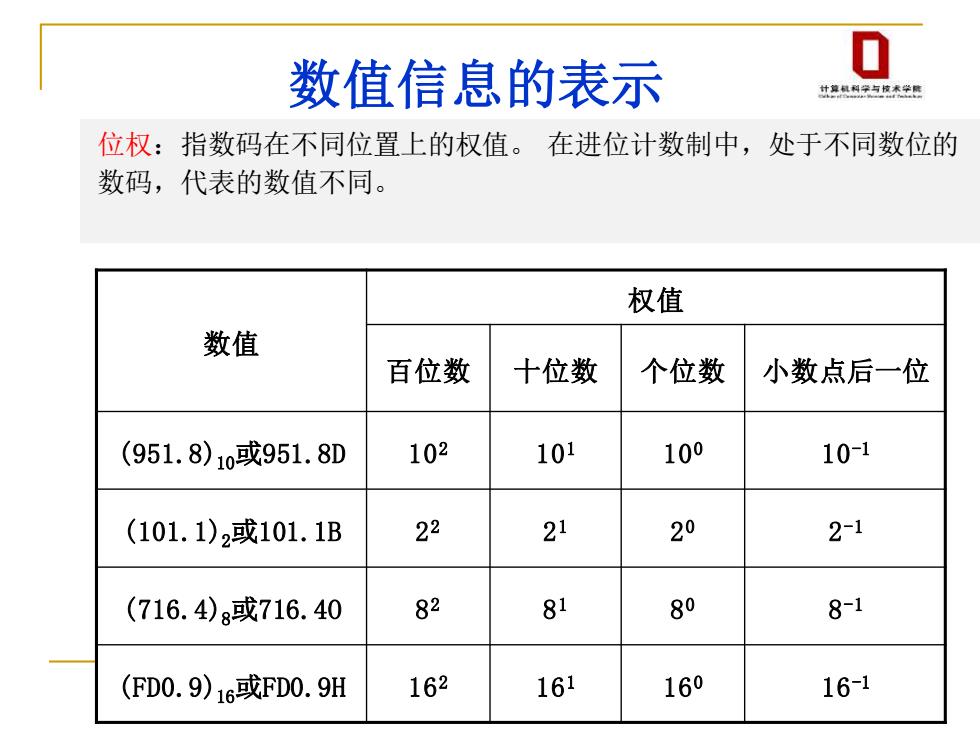
数值信息的表示 计具利学与学 位权:指数码在不同位置上的权值。在进位计数制中,处于不同数位的 数码,代表的数值不同。 权值 数值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (101.1)2或101.1B 22 21 20 2-1 (716.4)或716.40 82 81 80 8-1 (FD0.9)16或FD0.9H 162 161 160 16-1
6 数值信息的表示 位权:指数码在不同位置上的权值。 在进位计数制中,处于不同数位的 数码,代表的数值不同。 数值 权值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (101.1)2或101.1B 2 2 2 1 2 0 2 -1 (716.4)8或716.4O 8 2 8 1 8 0 8 -1 (FD0.9)16或FD0.9H 162 161 160 16-1

计草机利学与校术学网 数制 十进制数 二进制数 八进制数 十六进制数 数码 0~9 0~1 0~7 0~9,A~F,a~f 基 10 2 8 16 权 10°,10,102, .2,2,22, 8,81,82,. 16°,16,162, 表示 八进制:4275=4*83+2*82+7*81+5*8°61+14*16° 特点 逢十进 逢二进一 逢八进一 逢十六进一
数制 基 权 表示 数码 特点 10º ,10¹,10²,. 十进制数 0~9 10 逢十进一 二进制数 0~1 2 2º ,2¹,2²,. 逢二进一 八进制数 0~7 8 8º ,8¹,8²,. 逢八进一 十六进制数 0~9,A~F,a~f 16 16º ,16¹,16²,. 逢十六进一 十进制: 八进制: 十六进制: 二进制:4956= 4275=4*8³+2*8² +7*8¹+5*8º 1011=1*2³+0*2² +1*2¹+1*2º 81AE=8*16³+1*16² +10*16¹+14*16º 4*10³+9*10² +5*10¹+6*10º
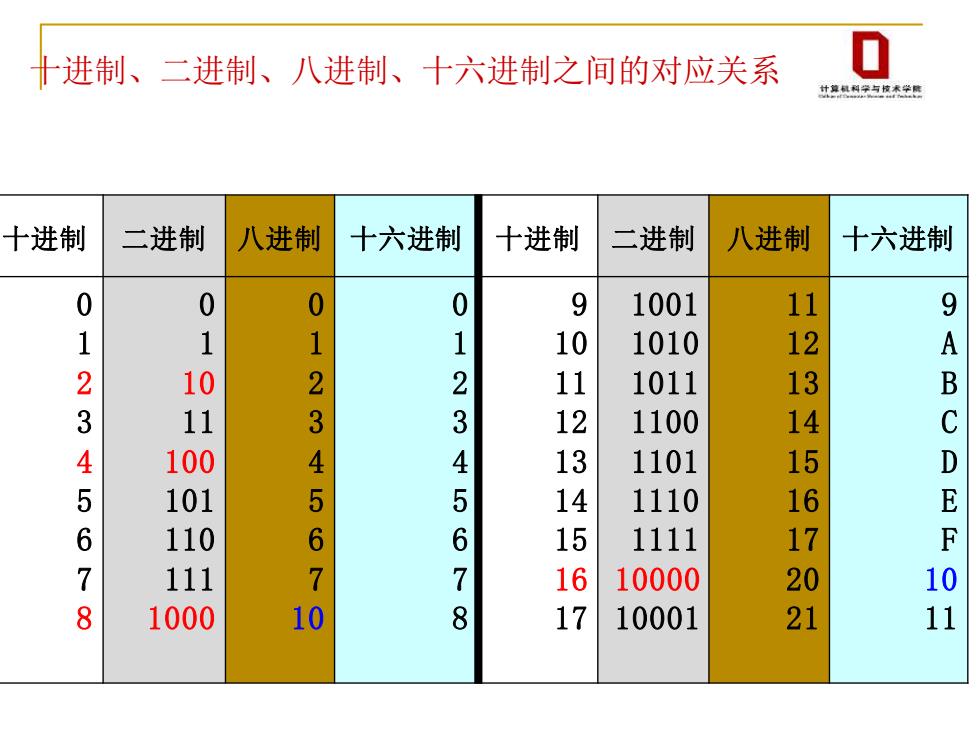
进制、二进制、八进制、十六进制之间的对应关系 凤利学与拉学脑 十进制 二进制 八进制 十六进制 十进制 二进制 八进制 十六进制 1001 110110020108 01234567 01 10 1010 112 012345678 1 1011 2345678 2 1100 134 1 1101 15 14 1110 1111 16 617204 9ABCDEF01 10000 10 17 10001
十进制、二进制、八进制、十六进制之间的对应关系 十进制 二进制 八进制 十六进制 十进制 二进制 八进制 十六进制 0 1 2 3 4 5 6 7 8 0 1 10 11 100 101 110 111 1000 0 1 2 3 4 5 6 7 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1001 1010 1011 1100 1101 1110 1111 10000 10001 11 12 13 14 15 16 17 20 21 9 A B C D E F 10 11

0 数制的转换 计草机利学与校术学网 ,二进制、八进制、十六进制数转化为十进制数 0 对于任何一个二进制数、八进制数、十六进制数可以写出它的按权展开式 ,再进行计算即可。 口例如: (1111.11)2 =1×23+1×22+1×21+1×20+1×2-1+1×22=15.75 (A10B.8)16 =10×163+1×162+0×161+11×160+8×16-1=41227.5
数制的转换 ➢ 二进制、八进制、十六进制数转化为十进制数 ❑ 对于任何一个二进制数、八进制数、十六进制数可以写出它的按权展开式 ,再进行计算即可。 ❑ 例如: (1111.11)2 = 1×2 3+1×2 2+1×2 1+1×2 0 +1×2 -1 +1×2 -2=15.75 (A10B.8)16 =10×163 + 1×162+ 0×161 +11×160 +8×16-1= 41227.5

十进制数转化为R进制数 杜算风利学与技本学脑 对于整数部分采用除取余法,即逐次除以R,直至商为O,得出的余数倒 排,即为R进制各位的数码。 示例1,:十进制转换为八进制 最低位 8 75 3 (75)=(113)为 8 9 1 (113)8 8 1 =1×82+1×81+3×80 最高位
十进制数转化为R进制数 对于整数部分采用除R取余法,即逐次除以R,直至商为0,得出的余数倒 排,即为R进制各位的数码。 (75)10=(113)8 示例1:十进制转换为八进制 75 9 1 8 8 8 3 1 1 0 最高位 最低位 (113)8 =1×8 2+1×8 1+3×8 0